低密度泡沫材料本构模型的UMAT实现

1. 低密度泡沫变形特点

我们都知道，低密度泡沫材料大都是多孔介质，这类材料在压缩时的变形很有意思。看下面这个图：

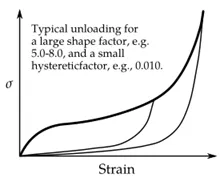
从图里很容易就能看出，随着载荷的增加，初始阶段变形线性增加，随后载荷-变形曲线趋于平缓，也就是说变形大了，力没上去。最绝的是，到后面，力又陡然升上去了。

这个现象主要因为，加载前期材料为弹性，随着变形的增加，此时泡沫的气孔开始被压垮，进入屈服，简单理解这个时候就是在压空气，因此力增加幅度不大。到后期，气孔压完了，泡沫被压实了，此时泡沫的密度变的很大，相当于硬化了，很小的位移都需要很大的力加载。

现象很有意思，但是如何用建立对应的本构就不容易了。目前主流的方法是，基于现有泡沫本构关系框架，通过试验确定里面的各项参数。而这个本构关系框架，也是大量的研究和试验拟合出来的。

LS-DYNA针对低密度泡沫使用的方法很有意思，类似于一种叠加法，把两种本构叠加起来实现上面描述的效果。

本文就介绍下LS-DYNA的低密度泡沫理论，并且通过ABAQUS UMAT实现。

2. 本构理论

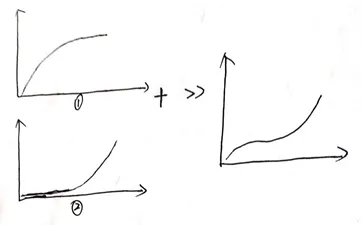
LS-DYNA是如何实现的呢？看下面的图就明白了。给出两种本构关系叠加：

1)       随着变形的增加，载荷先增加后趋于平缓；

2)       随着变形的增加，载荷一直增加，但是前期增加幅度小，后面载荷的增速不断变大；

3)       上面两种合在一起就是低密度泡沫的变形特点。

第一种本构描述如下：

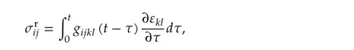
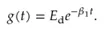
第二种本构描述如下：

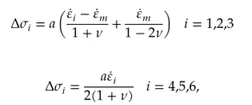
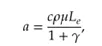
3. 算例

在UMAT中完成上述本构的编写。

3.1 模型

考虑立方体的压缩，如下图。

3.2 边界条件

考虑压缩工况，要特别指出的是，压缩的幅度要很大才能出完整的曲线，比如这个立方体边长是5，那压缩位移可以给到4.9。

3.3 结果

最终得到应力应变曲线如下，从图里可以看出，我们用UMAT自行编写的本构，可以很好的反映低密度泡沫的变形特点。

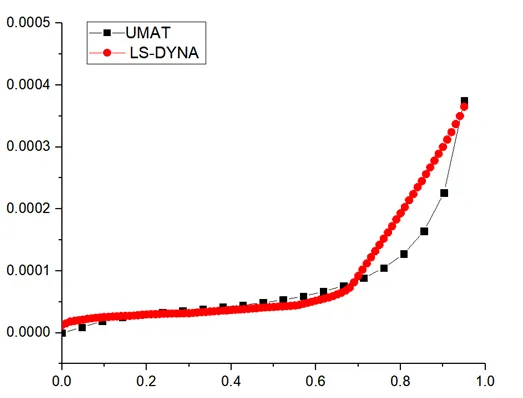
免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删