砂土刚度衰减模型在海上风电工程中的应用探讨

1. 工程背景

砂土是海上风电工程常见的土类，循环荷载作用下它的软化现象会引起桩侧土体塑性变形累积过大，极易造成结构失稳倾覆。Huurman提出的刚度衰减模型通过引入循环应力比将砂土刚度与循环次数连接在一起，是分析砂土地基构筑物循环承载工况的有效方法。砂土刚度衰减模型有较好的理论基础，难点在于将其内嵌于通用有限元软件的计算内核。

大型海上风电机组是大力发展风电、有效利用近海风能资源的核心技术，为提高机组的发电功率，风机尺寸通常较大，要求基础拥有较强的结构承载能力。大直径单桩基础、导管架基础以及负压筒基础因其优异的受力特性成为了海上风电工程常用的基础形式，它们不仅要满足竖向承载力的要求，更要在风、波浪以及洋流等循环横向荷载作用下保持结构稳定。

海上风电基础的有限元模型同时具有材料非线性、位移非线性（大变形）以及边界条件非线性（接触算法）的特性，对软件非线性求解的能力有着较高的要求。Abaqus因其优异的非线性求解器在海上风电工程中应用广泛，同时软件提供了二次开发程序的接口，允许用户采用FORTRAN计算机语言编写描述材料受力变形特性的子程序。笔者基于前人工作经验，采用Abaqus 建立了砂土地基中循环承载工况下，大直径单桩基础、负压筒基础以及导管架基础的有限元模型，编写了海上风电基础通用的USDFLD子程序与Abaqus 的求解器联立求解，实现了砂土地基刚度的衰减，并分析了其受力变形、位移~荷载曲线以及土体刚度的发展规律，研究成果可为海上风电设计参考。

2. 砂土刚度衰减模型

3. 程序框架

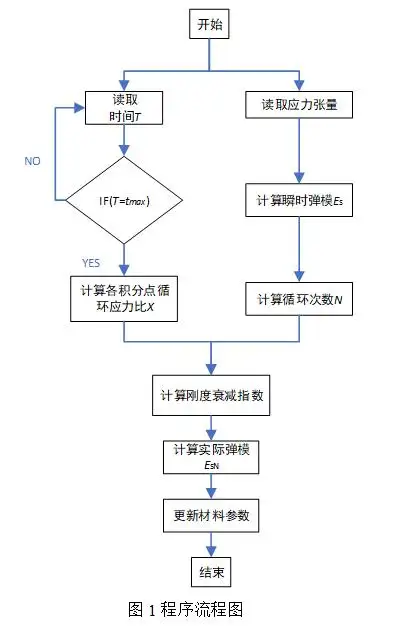
4. 有限元模型

4.1计算工况

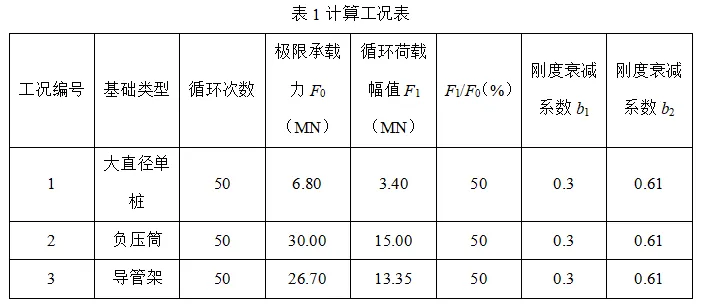
砂土刚度衰减模型程序是通用的二次开发程序，对各类结构形式的砂土地基都应得到较好的解答。大直径单桩基础、负压筒基础以及导管架基础是海上风电基础常用的结构形式，现采用ABAQUS软件建立这三类基础的有限元模型，与编写的二次开发程序进行联立求解，进而对程序的适用性进行验证，刚度衰减系数的取值参考现有文献资料（具体工况见表1）。

4.2模型基本假定

建立有限元模型时，对结构的适当简化能提高关键部位的计算精度，更能够减少计算机运算量，降低程序运行时对电脑硬件的要求。简化模型时应以不改变客观实际为基本原则，参考既有文献，有如下假定：

1）不考虑打桩和拖运等安装过程对桩身的影响；

2）土体为各向同性理想弹塑性材料，采用Mohr-Coulomb 本构模型模拟，桩为各向同性理想弹塑性材料，采用双线性本构模型模拟；

4.3几何模型

参考江苏沿海风场资料，各基础几何模型的参数列于表2，导管架基础上部结构与角桩结合，共分为两类，一类直径1.1m，壁厚0.032m，共16根；另一类直径0.8m，壁厚0.024m，共8根。角桩采用4根间距24m直径为3m的直桩，桩长75m，壁厚36mm。

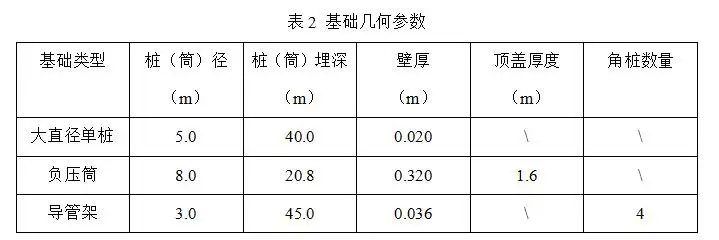
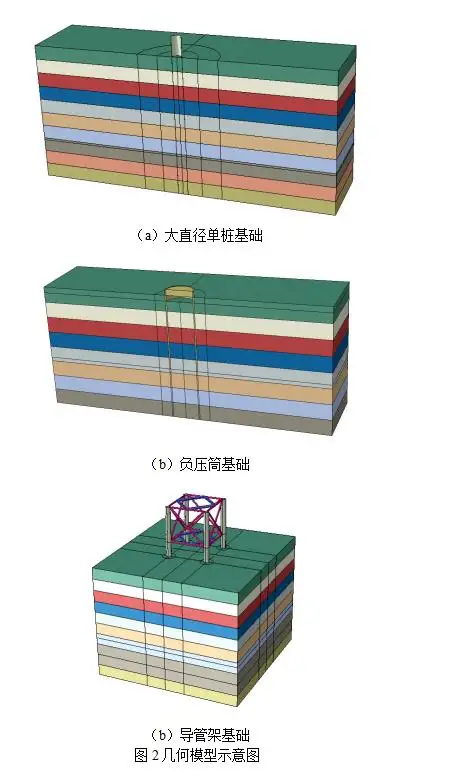
大直径单桩基础与负压筒基础均采用二分之一轴对称方式建模，导管架基础采用三维全模型方式建模。砂土的初始弹性模量会对计算收敛性存在较大影响，根据试算的应力数据将土层进行相应等分后分别赋予初始弹性模量（见图2）。

4.5边界条件

有限元模型需合理地设置边界条件，土体侧面约束径向位移，底面固接。计算模型在保证分析精度的条件下，应选取合适的地基土计算范围以减小计算量，大量的现场试验和数值模拟分析表明，沿加载方向，8倍直径（8D）范围外地基土的位移近乎为零，土体边界对数值分析的精度基本没有影响。横向荷载作用下桩端位移基本为零，周围土体变形较小，土体计算深度取1.4倍桩入土深度是合理的。本次研究土体计算范围的选取遵循上述准则，试算结果表明边界效应基本为零。

4.6单元选取与网格划分

模型的网格划分不仅影响着有限元分析计算的精确性，更对分析能否收敛起着决定性的作用。为避免二次积分单元造成接触计算不易收敛的问题，桩、筒和土体均采用减缩积分单元C3D8R，既能够缩减计算时间，也可以避免地应力回代时高斯积分点应力位于屈服面以外，采用三维梁单元模拟导管。较密的网格利于Abaqus迭代分析的收敛，也能够防止计算中出现沙漏现象，模型网格划分采取加密关键部位网格密度，适当放宽非关键部位网格密度的划分方案（见图3）。

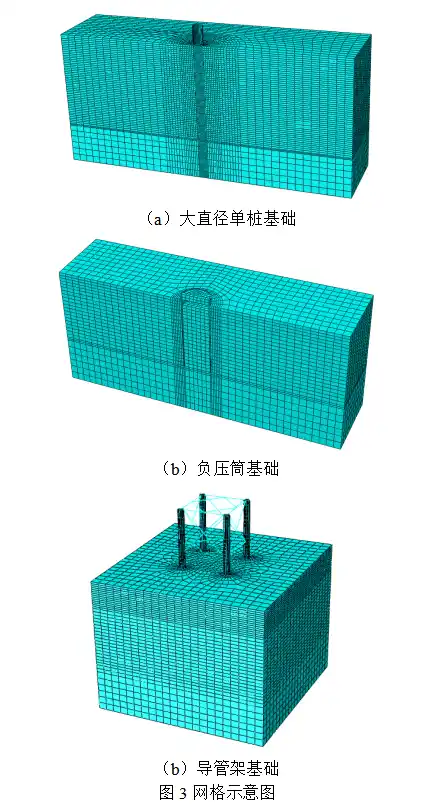
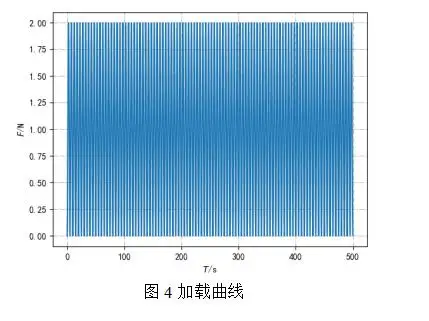
5. 计算结果

5.1受力变形分析

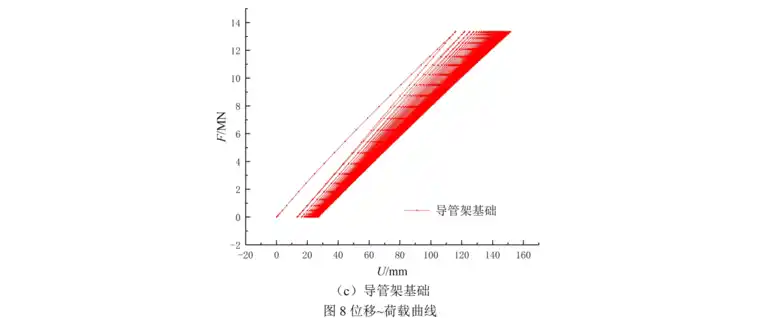
基础的受力变形分析是研究的重点，在后处理模块提取第五十次循环卸载后大直径单桩基础、负压筒基础以及导管架基础的位移和塑性应变云图（见图5~7）；提取桩（筒）顶部横向位移与荷载的关系曲线（见图8）。由图5~8可知，随着循环次数增加，砂土刚度逐渐减小，土体的累计位移增大，卸载后土体仍存在残余变形。表层受压侧土体因压缩变形过大进入塑性屈服阶段，非受压侧土体与桩（筒）呈脱离趋势，因砂土没有粘性，土体向脱离区域塌陷。相同荷载幅值下结构顶部位移随循环次数增大呈增大趋势，编写的子程序能较好地描述砂土地基的软化现象。

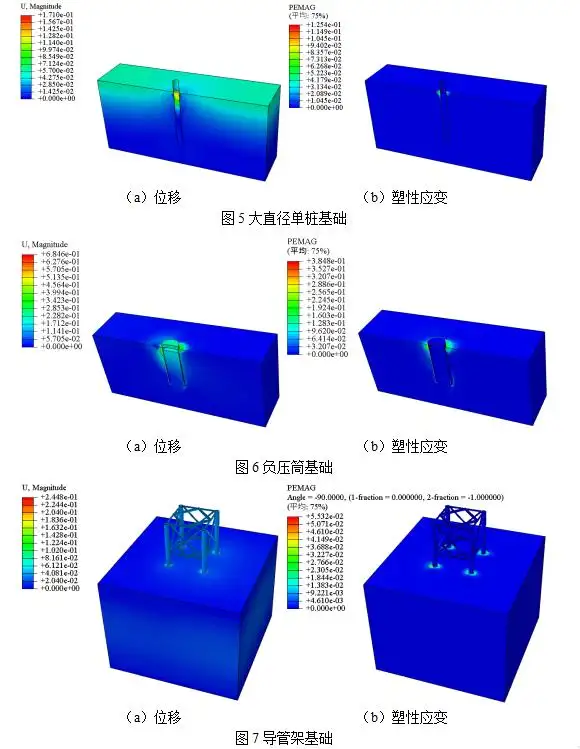
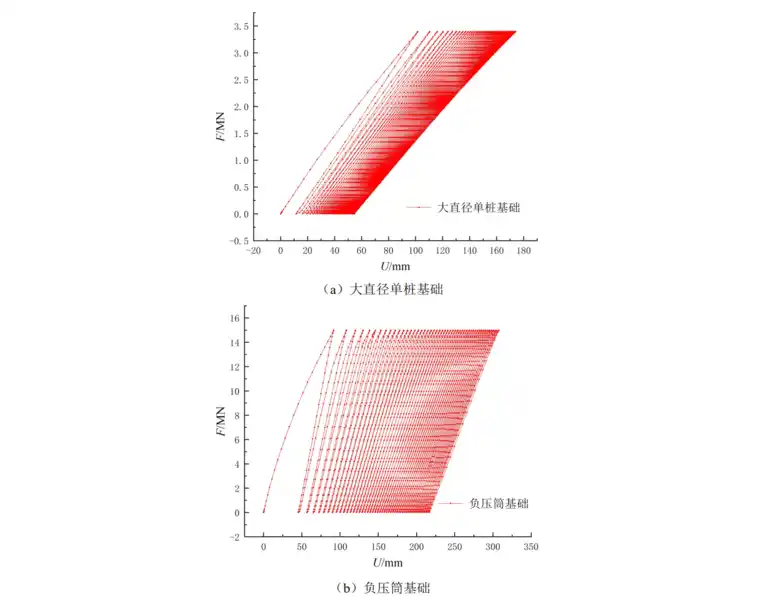
5.2刚度衰减系数分析

由式（5）可知，任意加载循环下砂土地基各材料积分点的瞬时弹性模量EsN与此时刻下基础的应力张量和刚度衰减系数K有关。在USDFLD子程序编译时加入材料的状态变量，将砂土地基材料积分点的刚度衰减系数K和瞬时弹性模量EsN作为第一状态变量（SDV1）和第三状态变量（SDV3）输出到ODB结果数据库内。

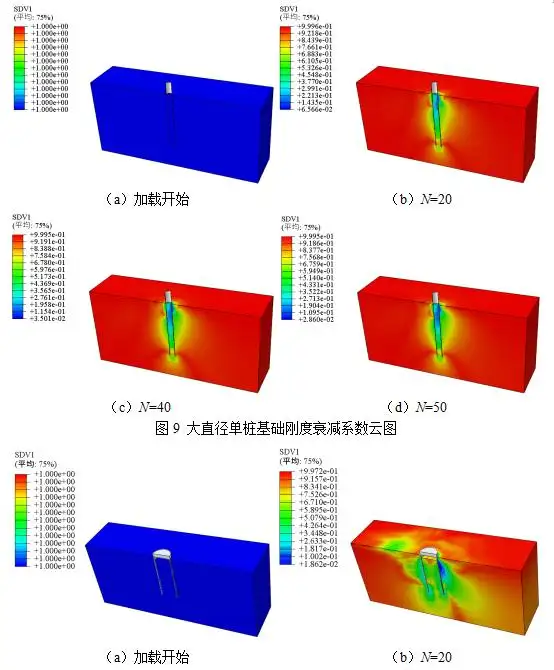
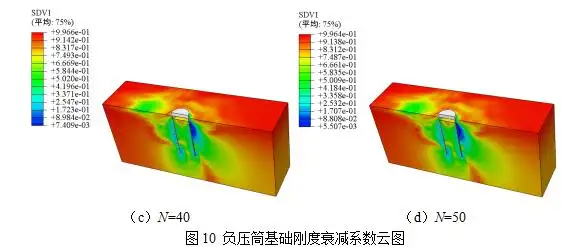
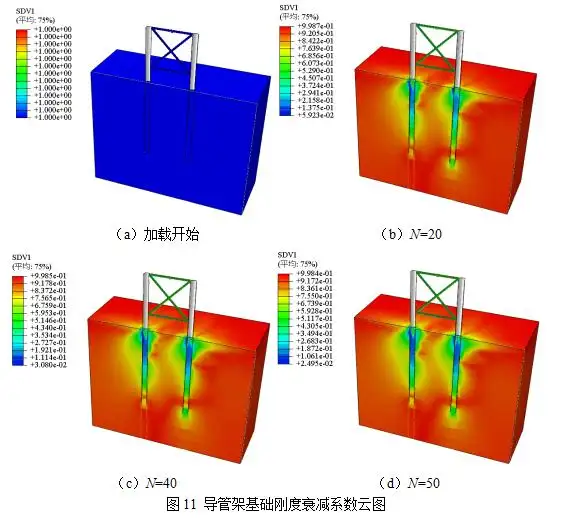
在后处理模块提取加载开始和第20、40和50次循环卸载时刻砂土地基的刚度衰减系数K（见图9~11）。由图9~11可知，刚度衰减系数K是实现砂土刚度衰减的关键参数，是一个与循环应力比Xc和循环次数N高度相关的复杂函数。式（5）表明，第一次循环时，刚度衰减系数K恒等于零，砂土刚度无需衰减。第一次循环的重点是提取加载峰值时刻地基土体各积分点的应力数据进而计算它们的循环应力比Xc。加载开始时刻尚未达到第一次循环的峰值，循环应力比数据为空（0），而刚度衰减系数K=1。同理，第一次循环后，循环应力比保持恒值不变，刚度衰减系数K恒小于1，且最小值位于桩（筒）侧相接触土体附近，并随循环次数增大而迅速减小。

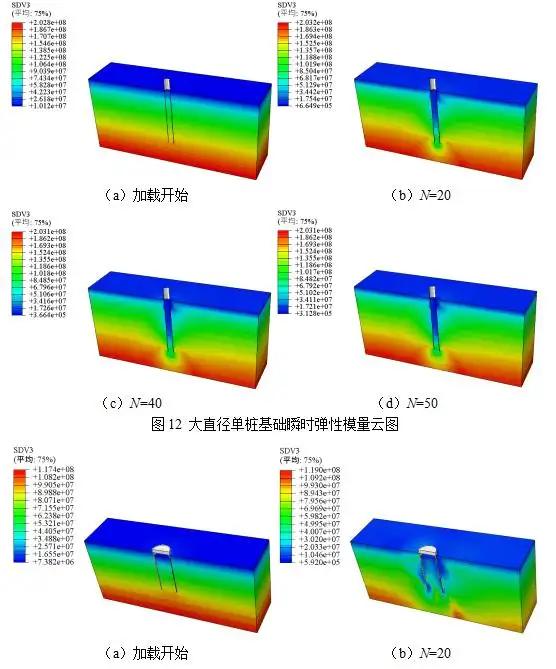
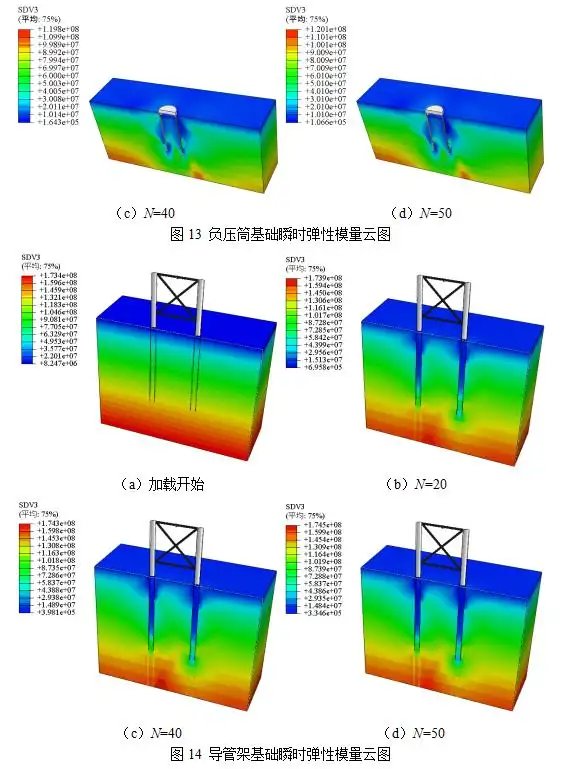
5.3瞬时弹性模量分析

在后处理模块输出加载开始和第20、40和50次循环卸载时刻砂土地基瞬时弹性模量（见图12~14）。由图12~14可知，加载开始时刻对应着地应力平衡分析步计算结束，地基土体的瞬时弹性模量与地基初始应力的分布规律基本一致，自地表近似呈线性向下增大。加载后，桩（筒）侧地基土体的应力状态发生改变，瞬时弹性模量根据应力状态重新分布，最大改变区域位于桩（筒）-土接触区域。当循环次数增大，砂土刚度衰减系数迅速降低，瞬态弹性模量随之减小，土体呈现软化趋势，编译的USDFLD子程序能较好地实现循环承载工况下砂土地基的刚度衰减。

6. 结语

砂土地基因其循环承载下特有的软化现象，采用常规的有限单元分析方法很难得到较合理的解答。本次研究基于大型通用有限元软件Abaqus的计算内核，采用FORTRAN计算机语言编写了砂土地基中海上风电基础通用的USDFLD子程序，通过引入砂土的刚度衰减系数将砂土的瞬时弹性模量与循环次数联系在一起，能较好地实现循环承载工况下砂土地基的变形累计与刚度衰减，并得到以下重要结论：

1） 循环承载工况下砂土的软化现象会导致结构的侧向变形随循环次数的增大而迅速提高，设计时需慎重考虑其影响。

2） 砂土刚度衰减模型是分析砂土地基循环承载工况的有效方法，采用FORTRAN编译的USDFLD子程序有较好的准确性和通用性。

3） 砂土刚度衰减模型实现的关键是对材料积分点应力张量的处理和循环次数的判定，由Abaqus求解器传递到USDFLD子程序内的计算参数能满足二次开发程序的所有输入需求。

4） 刚度衰减系数K是二次开发程序的本质参数，其计算公式内的参数b1，b2对K值影响较大，建议相关学者开展相应的土力学研究探求其具体规律。

计算机配置：

CPU:Intel(R) Core(TM) i7-10750H CPU @ 2.60GHz 2.59GHz(11核)

内存：32GB

计算耗时：

大直径单桩基础：9h

负压筒基础：12h

导管架基础：25h

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删