案例分享：iSolver下的开口钢管桩单轴压缩实验

一．模型背景：

该模型为开口钢管桩，该钢管桩的尺寸为：外直径2m, 壁厚0.05m, 桩长9m。桩所用钢为Q235钢，采用弹塑性本构模型，钢材密度为7.85t/m3, 弹性模量为215e6KPa, 泊松比为0.28，屈服强度为235MPa, 屈服后的应力应变关系为理想弹塑性模型。由于开口钢管桩具有轴对称性，故而只建立90度的模型，以降低计算成本。

图一：所建90度的开口钢管桩

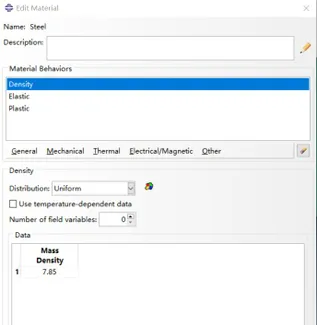
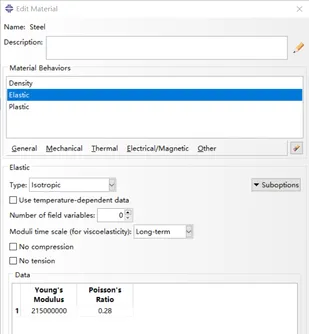
图二：钢材的参数设置

该模型的两个侧边截面为轴对称约束，桩底部固定，顶部受到均布荷载，压强为4000KPa。

图三：桩的边界约束及荷载

模型的网格类型采用C3D8R，将壁厚分为了两层。

图四：模型的网格划分

二．iSolver与Abaqus的结果对比

图五：桩内侧应力分布图（上侧：abaqus; 下侧：iSolver）

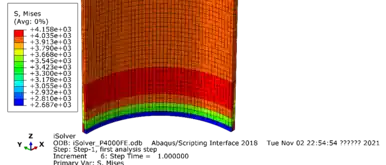
图六：桩内侧底部的应力集中图（上侧：abaqus; 下侧：iSolver）

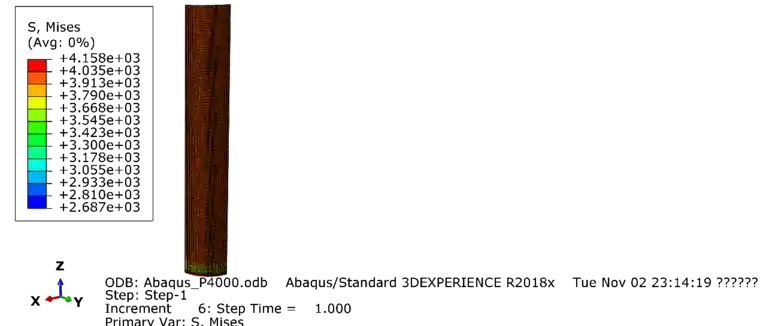
图七：桩外侧应力分布图（上侧：abaqus; 下侧：iSolver）

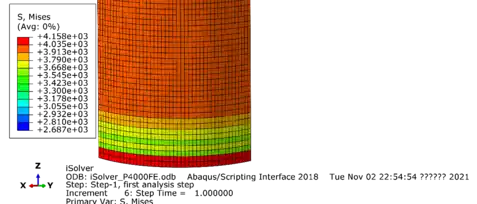
图八：桩外侧底部的应力集中图（上侧：abaqus; 下侧：iSolver）

取桩外壁的应力路径（图九）做桩的应力、应变及位移由桩顶部到桩底部的分布图。

图九：所取应力路径

a)Abaqus

b)iSolver

图十：桩轴向应力随深度分布图（x=0:桩顶；x=9:桩底部）

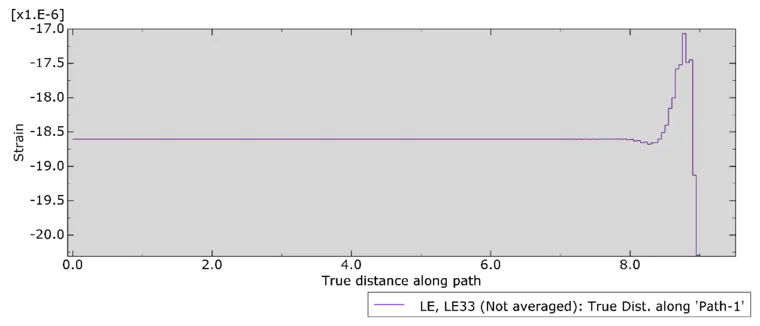
a) Abaqus  

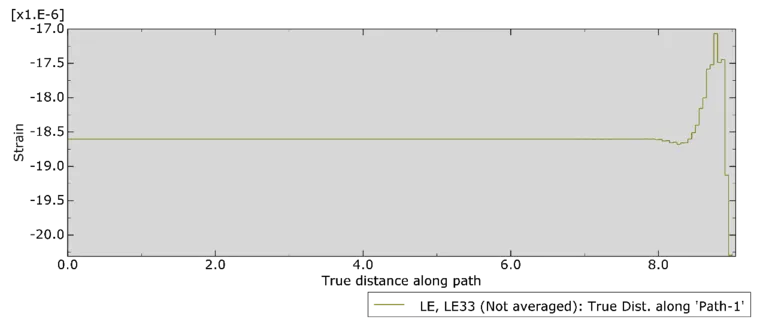
b)iSolver

图十一：桩轴向应变随深度分布图（x=0:桩顶；x=9:桩底部）

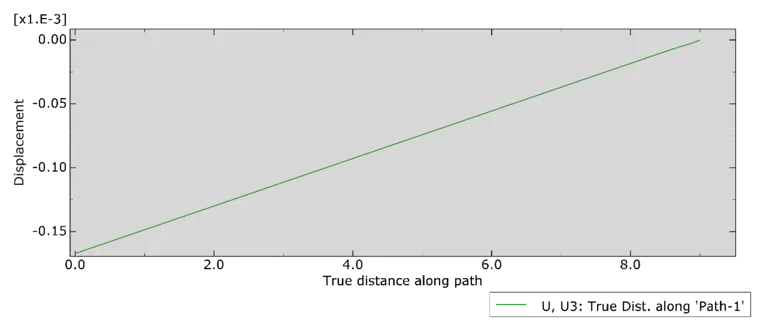
a) Abaqus        

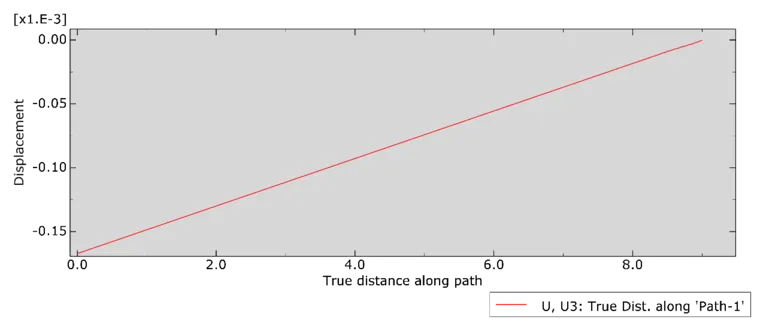
b)iSolver

图十二：桩轴向位移随深度分布图（x=0:桩顶；x=9:桩底部）

由分析可见，iSolver所得结果与Abaqus的精度近乎一致。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删