ABAQUS断裂参数K和J提取插件使用指南

在ABAQUS中计算断裂参数K和J经常会用到围线积分即contour integral，软件中有单独计算围线积分的模块，当然，在xfem（3D时）和debond（使用临界应力、临界裂纹张开位移、裂纹长度与时间准则时）中也可用计算围线积分

计算得到的围线积分通常输出到dat文件中，我们需要打开dat文件挨个查询裂纹每个分析步的每个增量步下的每个裂纹尖端的K1/K2/J值，这样操作起来十分繁琐，更不用说是提取这些结果到一个文件中再进行数据处理得到自己想要的曲线了。对于xfem计算2D模型时不能输出K和J的问题，simwe一个帖子给出了解决办法：http://forum.simwe.com/forum.php?mod=viewthread&tid=1113324&extra=&highlight=xfem&page=1

但是帖子中也明确地给出了：只能算最后一个increment的J和K的限制，那么如果我们需要提取每个分析步的每个增量步结果该怎么办呢，根据帖子中给出的插件代码，进行了大幅度的添加修改，最后进一步完善了该插件，可以提取每个分析步的每个增量步结果，另外还可以在程序中自己定义复合应力强度因子等参数，直接输出到屏幕，十分简单便捷，效率也非常高，省去了大部分处理数据的时间，下面就详细介绍其使用过程：

事先我们已经计算了一个2D三角形单元的围线结果，围道区域使用四边形单元（裂纹尖端使用了具有1/2奇异性的collapse单元），

odb云图如下：

此时，打开插件：

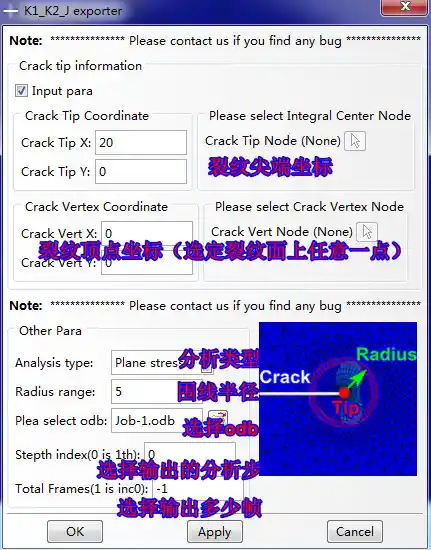
进行如下设置：

只演示对右裂纹尖端的提取：

1 从插件中计算出来的结果：

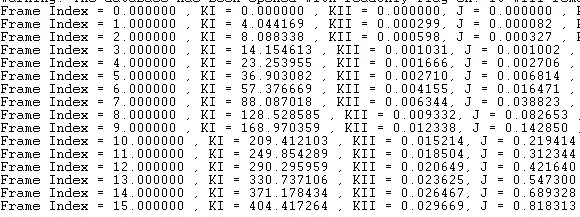
3 从dat文件中提取的结果：

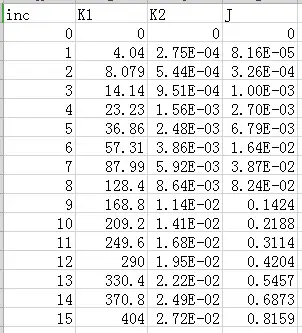
结果对比图：

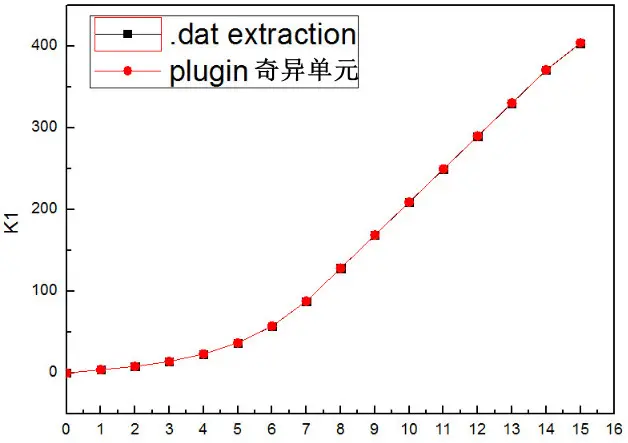
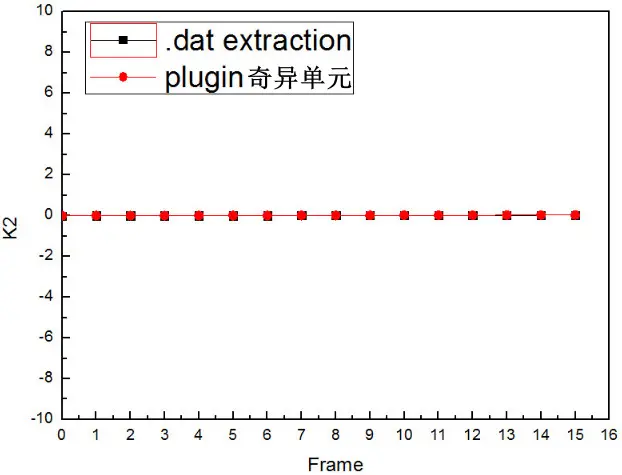
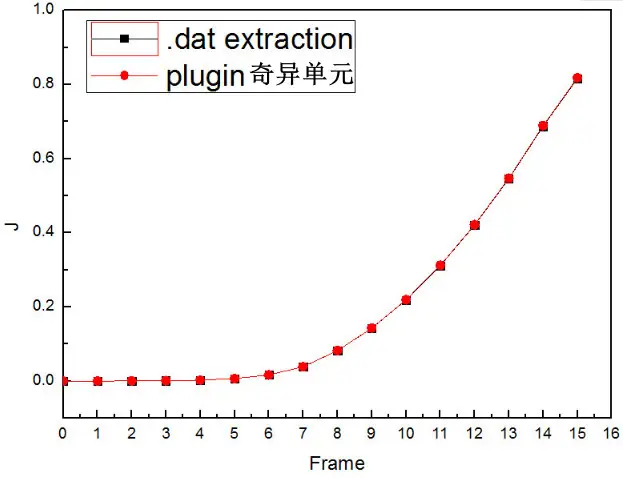
注意：因为时间步长是自动的，所以并不是每个Frame的时间步是相等的，而是开始很小，随后基本稳定（如下图所示），

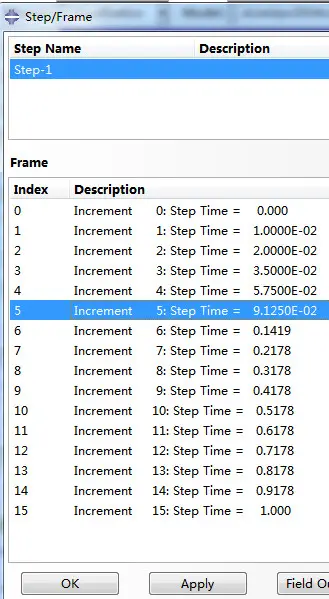
如此，导致断裂参数K和J的变化呈现出如图的增长方式，如果把时间步长固定，那么K和J随Frame将是线性增加的，如下图所示（云图的缩放因子为50），

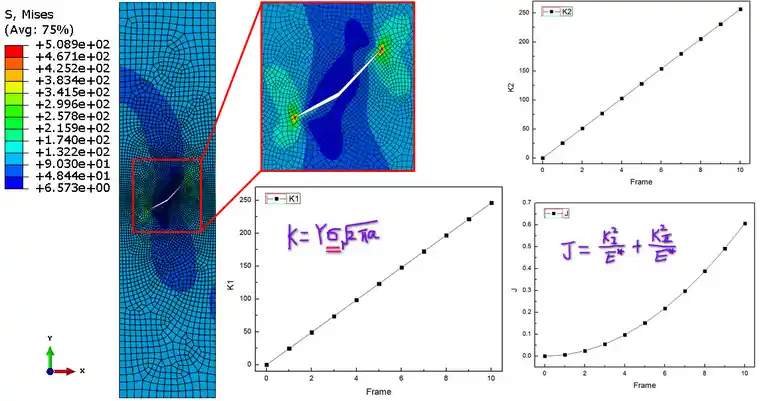
通过分析可知，对于K1/K2/J的结果插件计算的和从dat中提取的结果几乎完全一致，充分证明了插件的有效性；

**********************

下面又通过使用纯四边形一阶单元和二阶单元进行计算，然后通过插件提取结果，与ABAQUS使用奇异单元的计算提取的dat文件结果进行对比，结果如下：

纯四边形CPS4

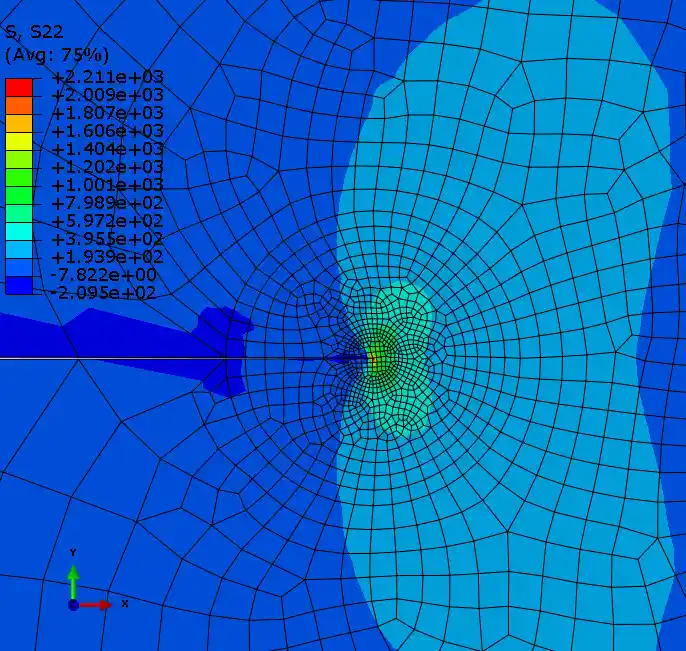
纯四边形CPS8

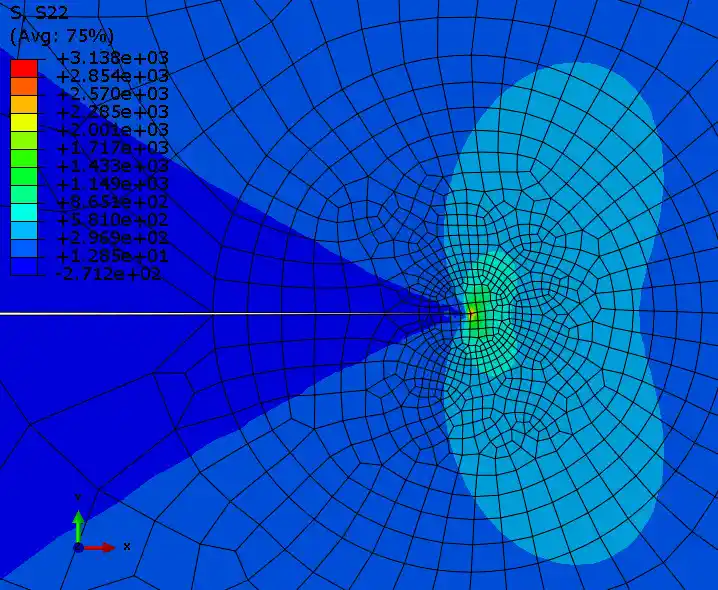
结果对比

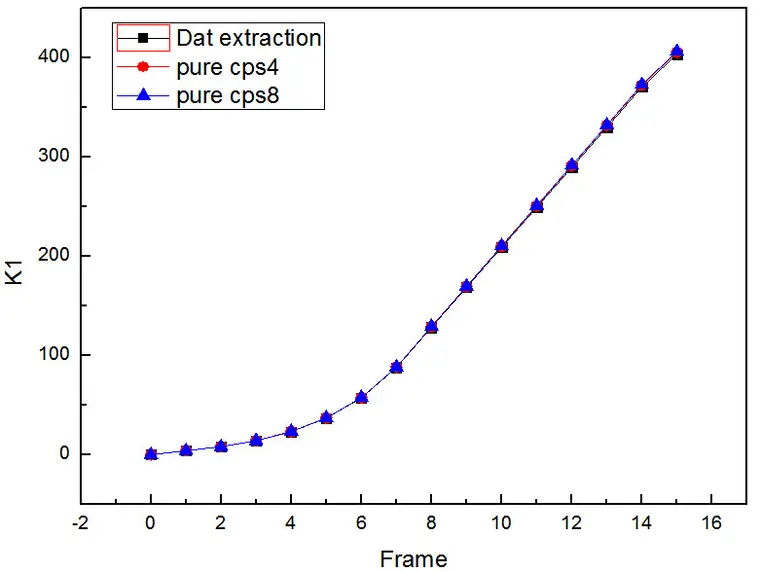
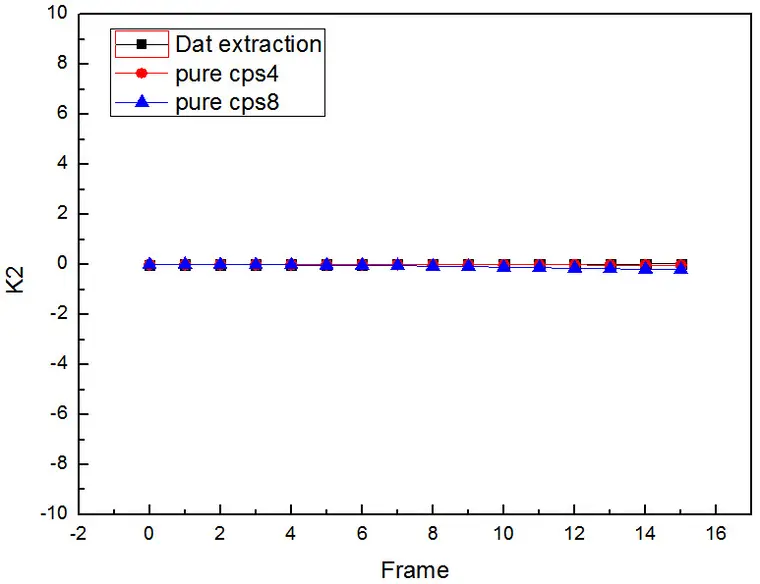
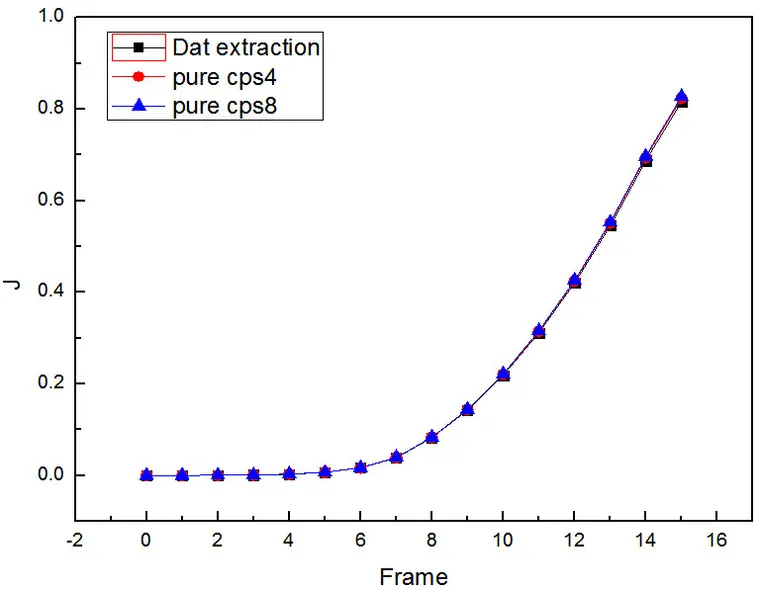
下面分析了采用不规则四边形单元下不同网格密度对结果的影响：

单元数为5500

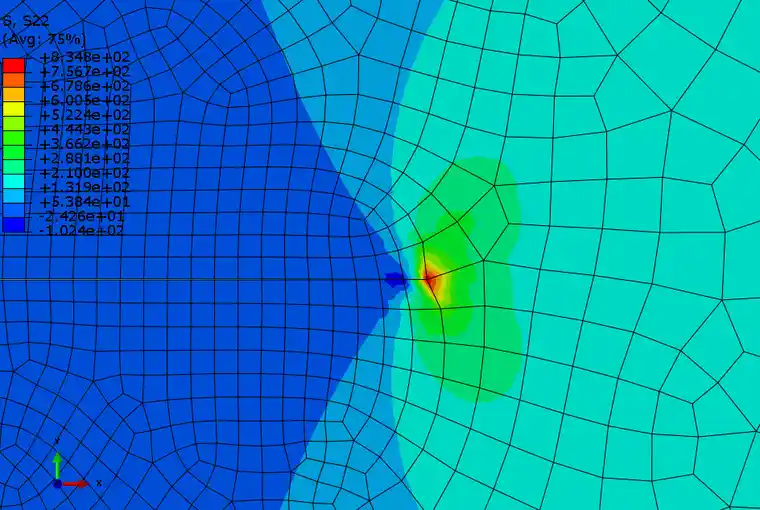
单元数为15000

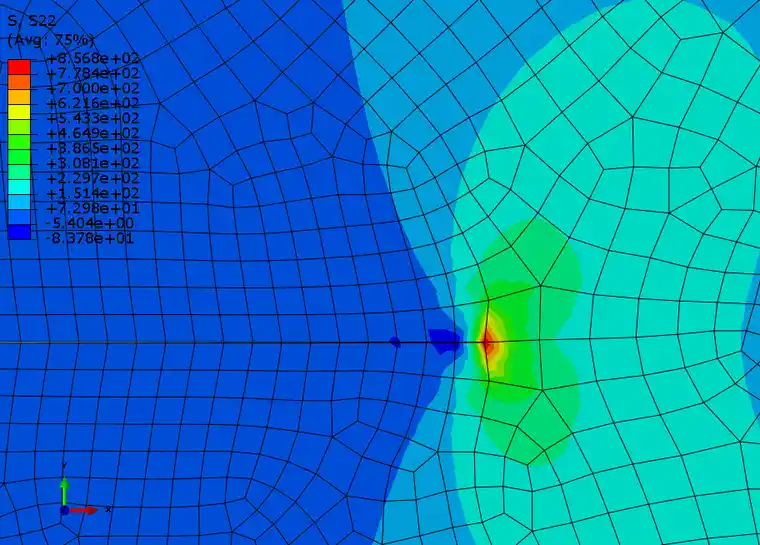
单元数为75000

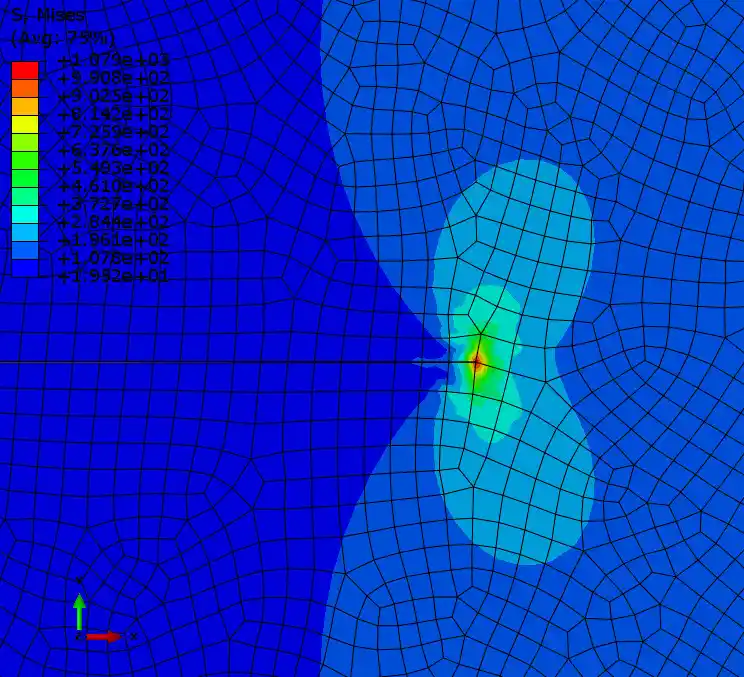
结果对比：

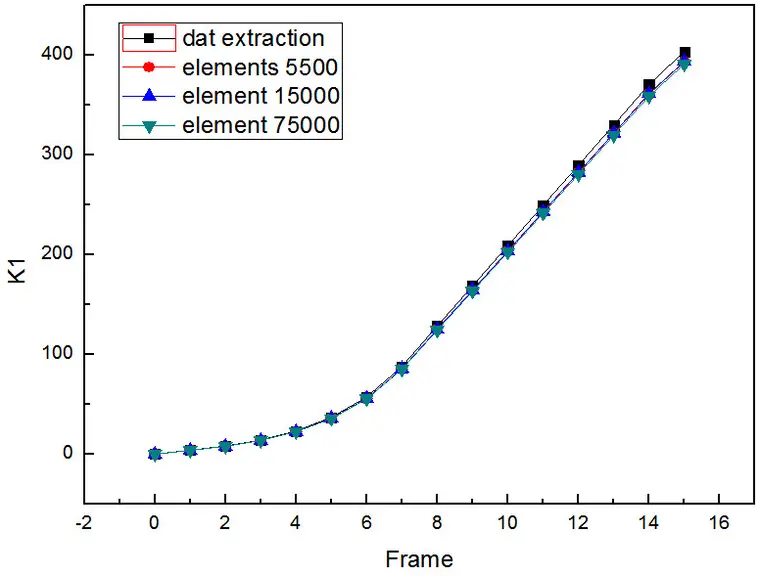
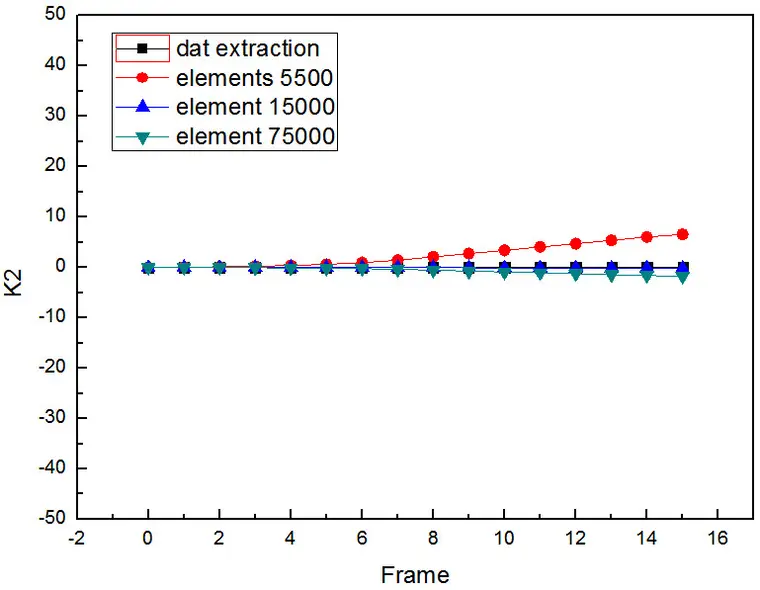
结果表明：单元数量太少，误差比较大；单元数量适中不但结果误差较小，而且计算效率也更高；

************************

另外，我们也对斜裂纹进行了对比分析，使用ABAQUS自带的围线积分计算时采用了具有1/2奇异性二阶单元，而对于使用插件时采用了普通的四边形CPS4单元，也对不同的提取半径进行了对比，结果发现结果对围线半径无关（这也是理论决定的），我们取三个不同的提取半径结果的平均值，发现提取半径取初始裂纹的1/10时与整个平均值基本吻合，事实上，之后的分析我们都可以提取半径为初始裂纹1/10时的结果作为参考，对于斜裂纹的结果分析如下：

ABAQUS计算采用奇异单元的结果：

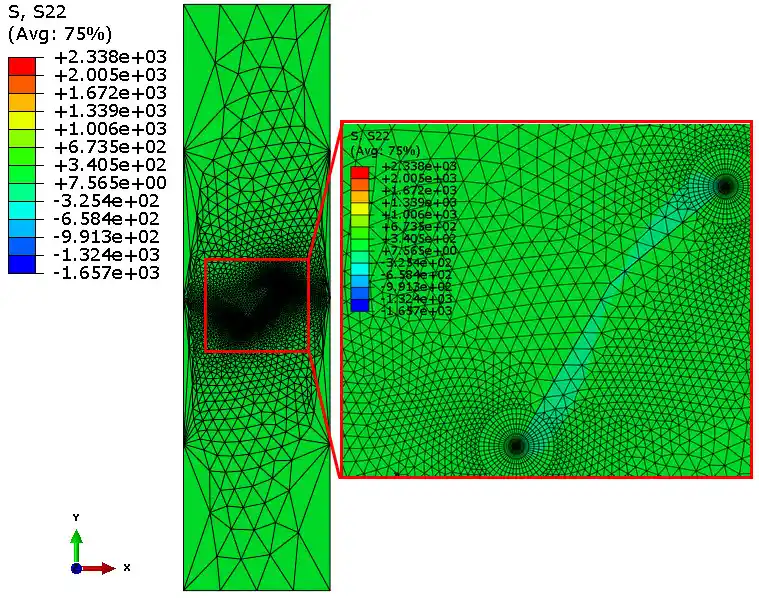
插件计算采用的普通四边形单元的结果：

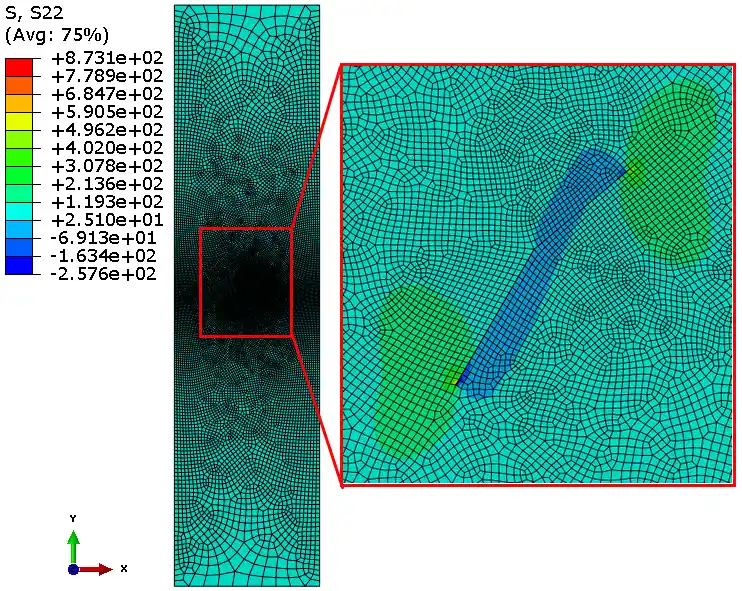
断裂参数对比：

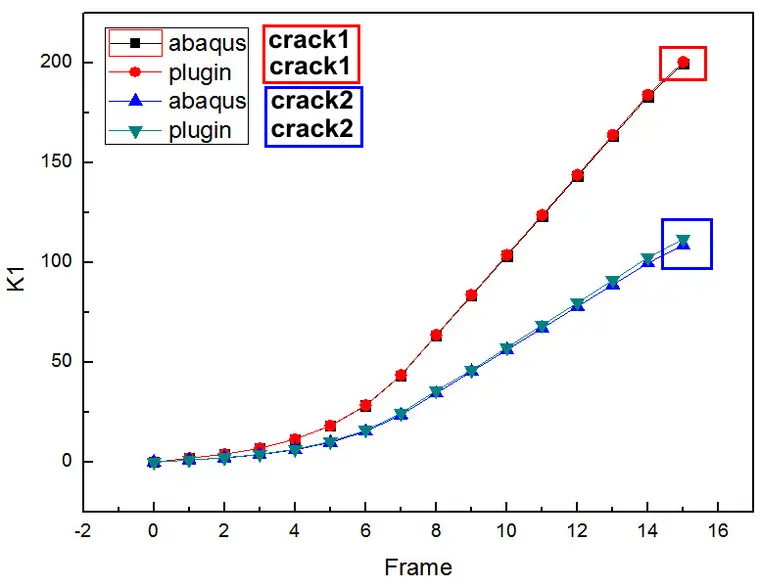
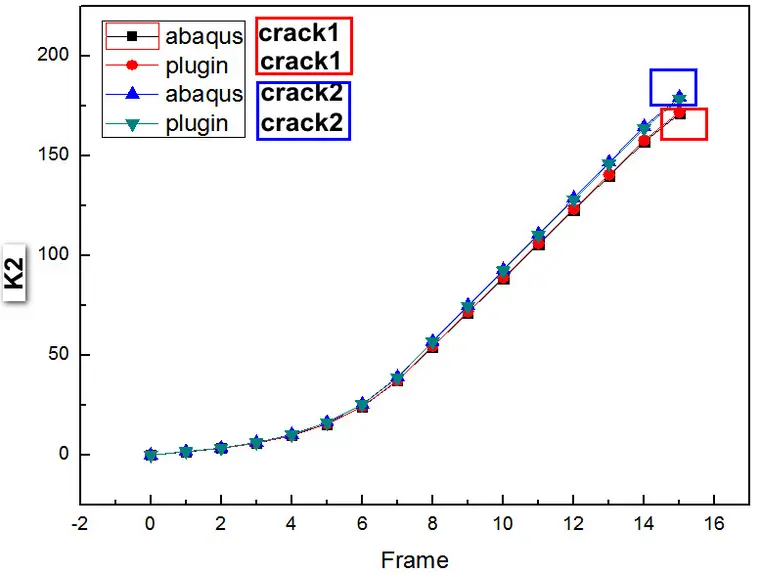
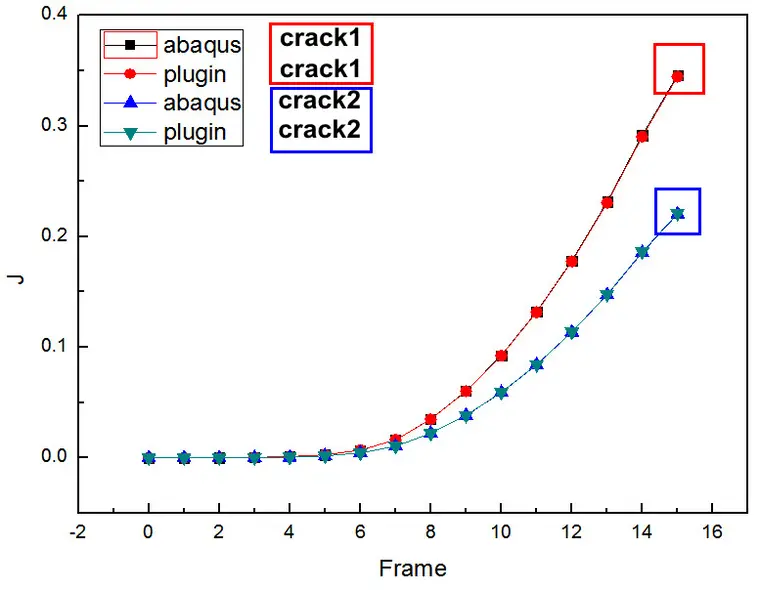
二者结果吻合非常好。

对于裂纹扩展角度也无需进行对比分析，因为它是由K1和K2推导而来的

对于xfem裂纹来说也同样可以采用插件进行提取。

最后总结一下，裂纹尖端应力强度因子的数值和理论计算方法（对于线弹性材料而言）：

静止裂纹：

1 二次开发插件（2D），通过应力场直接获取K；

2 abaqus自带contour integral（2D和3D）；直接获取K；

3 debond_vcct（2D和3D）获取G，然后转换为K；

4 xfem_LEFM（3D）获取G，转换为K；

  通过二次开发插件（2D）直接获取K；

运动裂纹：

1 contour integral+remeshing（2D和3D），输出裂纹扩展过程中裂纹尖端的K；

  contour integral+remeshing+map solution（2D和3D），输出裂纹扩展过程中裂纹尖端的K；

2 debond_vcct（2D和3D），输出裂纹扩展过程中裂纹尖端的G，然后转换为K；

  debond_（critical stress、critical COD，crack length-time）输出裂纹扩展过程中裂纹尖端的K；

3 xfem_LEFM（2D和3D），输出裂纹扩展过程中裂纹尖端的G，然后转换为K；

计算K和J的理论方法：

基于局部位移和应力

1 应力外推法（直接得到K1/K2）

2 位移外推法（直接得到K1/K2）

基于能量

3 J积分（区域积分法）（直接得到J）

4 全局虚拟裂纹扩展法（直接得到G）

5 局部虚拟裂纹扩展法（直接得到G1/G2）

6 虚拟裂纹闭合法（直接得到G1/G2）

借助辅助场

7 相互作用积分法（直接得到K1/K2/J）

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删