Abaqus/Explicit增量步步长确定技巧系列

如图：

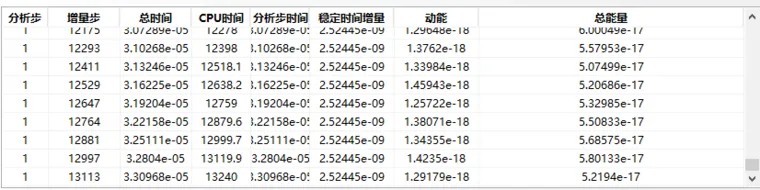
这是一个典型的监视器图，从这个监视器中可以看到，采用的是Explicit ，增量步为2.5e-9.对于时间总长为1s，或者0.1s的分析来说，明显太长了。那么到底是什么原因造成的呢？

什么是稳定极限值?如何确定稳定极限值?影响稳定极限值大小的因素有哪些?

默认情况下,ABAQUS/Explicit在分析过程中的增量步大小完全由求解器自动控制,即分所过程中是有条件稳定的,增量步必须小于某个极限值,以保证加速度在每个增量步中尽量接近常数,这样才能对速度和位移进行精确积分,此极限值称为稳定极限值(syhm),即分析所允许的最大稳定增量步长。它是ABAQUS/Explicit分析必须考虑的重要因素之一。为了提高求解效率,ABAQUS/Explicit在分析过程中总是尽可能选取稳定极限值作为增量步长。

确定稳定极限值的方法有两种:单元-单元估计法和总体估计法。ABAQUS/Explicit总是先根据单元-单元估计法估计稳定极限值的大小,然后在某些特定条件下跳转到总体估计法确定稳定极限值。

单元-单元估计法比较保守,它给出一个比实际的稳定极限值更小的稳定增量步长。一般情况下,模型中的各种约束和接触关系都有抑制特征值频谱的效应,单元-单元估计法不考虑这些因素的影响。

总体估计法采用当前扩张波速估计整个模型的最大频率w_max,在分析过程中不断地更新最大频率的估计值。总体估计法算得的稳定增量步长往往超过单元-单元估计法算得的稳定增量步长。总体估计法确定稳定极限值△t_stable的计算公式为:

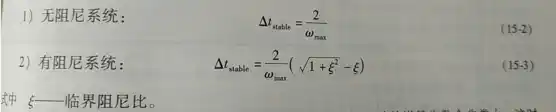
对于高阶振动问题,w_max,较大,因此稳定极限值较小,总的增量步数会非常大,这时ABAQUS/Explicit会通过引人体积粘性(bulkviscosity)的方法来引入一个小的阻尼。模型的高阶频率取决于多种复杂因素,其准确值是不可能获得的。采用保守的单元单估计法,稳定极限值重新定义为以下形式：

由上述公式可以看出,影响稳定极限值大小

1)材料密度

根据式(15-4)和式(15-5),密度越大,材料的波速c_d就越小,稳定极限值也就越大。采用质量缩放(massscaling)技术人为地增大材料密度,可以增大稳定极限值,节省分析时间。例如,复杂模型的局部区域可能包含非常小或形状很差的单元,这些单元即使数量很少,也可能决定稳定极限值的大小。

如果对这些单元进行质量缩放,可以很明显地节省分析时间需要注意的是,采用质量缩放技术增大材料密度会增大动态分析的惯性效应,如同增大了加载速率。如果质量缩放系数过大,会导致错误的分析结果。选择质量缩放系数的方法和选择加载速率的方法是类似的,都要保证不影响动态分析结果的精度。在ABAQUS/CAE中定义质量缩放的方法为,在Step功能模块中创建显式动态分析步时,单击Massscaling标签进行定义。

2)材料特性

根据式(15-4)和式(15-5),材料特性也会影响稳定极限值的大小。对于线弹性材料,其弹性模量是常数,因此材料的波速也是常数;对于非线性材料(例如金属塑性材料)随着材料的屈服,刚度会变小,导致波速减小，稳定极限值会随之增大。

3)单元网格

根据式(15-4),稳定极限值与最小单元尺寸成正比,即使模型中只有一个很小的或者形状扭曲的单元存在,都会大大降低稳定极限值,增加计算时间。为了增加定增量步长,加快分析速度,不应划分过于细化的网格,但同时要注意,过粗的网格会降低分析结果的精度。

实际建模过程中,应在保证分析精度的前提下,选择适当的网格密度相应尽量保证单元形状是规则的。ABAQUS/Explicit在STA文件中列出了稳定极限值最小的10个单元,可以查看这些单元所在的位置,改进相应区域的网格,或在这一区域使用质量缩放技术。

4)单元类型

如果分析过程中增量步长超过稳定极限值,可能会出现数值不稳定现象（nummerical instability),导致异常的计算结果。ABAQUS/Explicit对于绝大部分单元都能够保数值稳定。但是,如果模型中包含弹簧单元和阻尼器单元,就有可能出现数值不稳定,这会看到不符合物理规律的计算结果,而且解往往是振荡的。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删