1.概述
简要介绍:One Millisecond Face Alignment with an Ensemble of Regression Trees算法(以下简称GBDT)是一种基于回归树的人脸对齐算法,这种方法通过建立一个级联的残差回归树(GBDT)来使人脸形状从当前形状一步一步回归到真实形状。每一个GBDT的每一个叶子节点上都存储着一个残差回归量,当输入落到一个节点上时,就将残差加到改输入上,起到回归的目的,最终将所有残差叠加在一起,就完成了人脸对齐的目的。
在逐步详细介绍GBDT之前,按照惯例,先介绍人脸对齐的基本概念和原理。
人脸对齐中的几个关键词:
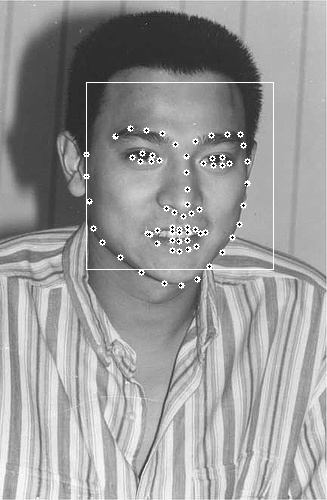
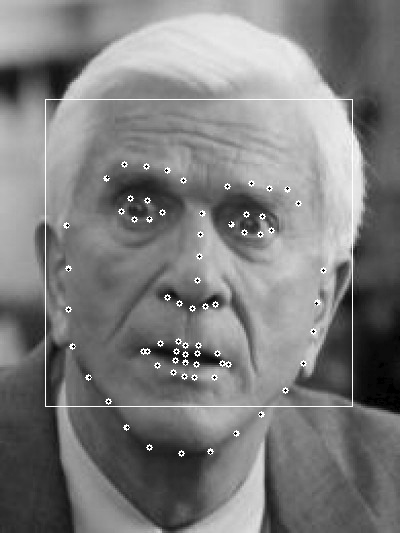
形状(shape):形状就是人脸上的有特征的位置,如下图所示,每张图中所有黄点构成的图形就是该人脸的形状。
特征点(landmark):形状由特征点组成,图中的每一个黄点就是一个特征点。

人脸对齐的最终目的就是在已知的人脸方框(一般由人脸检测确定人脸的位置)上定位其准确地形状。
人脸对齐的算法主要分为两大类:基于优化的方法(Optimization-based method)和基于回归的方法(Regression-based method)。
本文的方法属于基于回归的方法。
树的思想在机器学习算法中可谓是鼎鼎大名,非常常用的决策树、二叉树等,以及由树构成的随机森林等算法,都在各种领域被广泛使用,甚至延伸出了诸如“随机蕨”等类树的结构。树不仅多种多样,其应用也绝不仅仅局限于分类,例如本文就将树的思想应用在回归的领域,而非常流行的CART分类回归树也是其中一种,甚至还有采用树的结构来提取特征的方法(3000FPS)。
如果大家理解随机森林,那么对本文的GBDT可能会更好理解一点。简单来说随机森林就是将很多棵决策树联合在一起,其中每一棵树的训练采用的是随机数量的样本和随机的特征,其实也是集成学习的思想的表现之一。
而本文的GBDT,相比与随机森林,其实本质上差别不是很大,主要差别在于:
1)每一棵树之间的关系是串行的,并非是并行的关系,也就是说后一棵树的建立在前一棵树的基础之上。
2)每一棵树的叶子节点上存的是残差,这也是GBDT的特点之一,也只有通过叶子节点上保存的残差,才能使形状不断地回归,从而回归到真实形状。
下面直接介绍这种方法。
假设我要开始构建一棵GBDT,注意,这里的一棵GBDT的概念不是指一棵树,而是指很多棵树,很多棵树构成一个GBDT,所以说GBDT的地位类似与随机森林,都是由树集成构成的。
构建一棵GBDT要实现的目的是:通过这棵树,将人脸的初始形状回归到其真实形状上去(这是测试时的目的,训练时,也就是构建树时我们是知道其真实形状的,那么目的自然就是用GBDT来表示初始形状和真实形状的关系)。
假设我们一共有N幅图像,将它们作为训练样本,我们知道这N幅图像的每一个真实形状。首先我们要获得一个回归的初始形状,假设我们用所有图像的平均形状来作为这个初始形状(初始形状就是回归的起点,之后在测试时无论给出怎样一幅图像,我们都通过这个初始形状来进行预测和回归)。在原论文中,在训练时,作者并非只使用了初始形状,而是随机挑选另一个真实形状来作为某一幅图像的初始形状,这种做法我们先不讨论,首先讨论如何构建一棵GBDT。
现在开始构建GBDT的第一棵树。
有了初始形状,这里就会发现一个问题,假如使用平均形状来作为每一幅图像的初始形状,那么对所有图像来说,初始输入都是相同的,这如何分裂树呢?是的,对所有图像来说,初始形状相同,但我们分裂树时,采用的输入并非是当前形状,而是依据当前形状从该图片中提取出的特征。对于每一幅图像来说,初始形状虽然相同,但每一幅图片都不同,因此提取出的特征也就不同,论文中是使用的像素差作为特征,下一节会详细讲这种特征的提取方式。我们依据特征来进行节点的分裂操作,直至到达树的叶子节点。
当我们把N张图片都输入这第一棵树,自然每一张图片最终都会落入其中的一个叶子节点,比如第1张图片落入了第3个叶子节点,第2张图片落入了第1个叶子节点,第3张图片落入了第三个叶子节点等等。这样,每一个叶子节点中都会有图片落入,当然也可能没有,这无所谓。这时,我们就要计算残差,计算每一个图片的当前形状和真实形状的差值,之后,在同一个叶子节点中的所有图片的差值作平均,就是该叶子节点应当保存的残差。当所有叶子节点都保存了残差后,第一棵树也就构造完毕了。
在构造第二棵树之前,我们要把每张图片的当前形状做一个更新,也就是要将当前形状更新成:当前形状+残差。对应到第一棵树,即是初始形状加上残差,这样每一张图片的当前形状就从初始形状变成了初始形状加残差,距离真实形状又更近了一步。
之后再用同样的方法构建第二棵树,依据特征进行节点分裂,直到叶子节点。在叶子节点中计算每一张图片当前形状和真实形状的差,然后取平均,将这个平均值保存在该叶子节点中,作为残差。之后更新每一张图片的当前形状,即将叶子节点中保存的残差加上其当前形状,作为新的当前形状,然后就可以建立第三棵树了。
直至建立的树足够多,可以最后的当前形状表示真实形状,那么这一个GBDT也就建立完成了。
还有一个问题没有解决,那就是GBDT中的每一棵树是怎样分裂的,下面详细叙述分裂的方法。
对于一棵GBDT(很多棵子树构成)而言,我们要建立一个特征池,这个特征池里是我们随机挑选的一些点的坐标,然后对于每一幅图像,这些点都对应着不同的像素值,因此,在树的节点分裂时,我们首先会在这合格特征池中随机挑选两个点,然后计算每一张图片在这两个点处的像素值,然后计算每一张图片的这两个点处的像素值的像素差,之后随机产生一个分裂阈值,根据这个阈值进行判断,如果一幅图像的像素差小于这个阈值,就往左分裂,否则往右分裂,将所有图片都这样判断一次,就将所有图片分成了两部分,一部分在左,一部分在右。我们重复上面这个过程若干次,看看哪一次分裂的好(判断是否分裂的好的依据是方差,如果分在左边的样本的方差小,这说明它们是一类,分的就好),就把这个分裂的好的选择保存下来,即保存下这两个点的坐标值和分裂阈值。这样一个节点的分裂就完成了。然后每一个节点的分裂都按照这个步骤进行,直到分裂到叶子节点。
6.作者的实验结果
原论文作者一共建立了10棵GBDT,每一个GBDT中包含500棵树,10棵GBDT的意思就是,每一棵GBDT都是相互独立的,一共有10个相互独立的特征池。作者的每一个特征池中有400个点,在同一棵GBDT中,每次节点分裂,都从这400个点中挑选出20对点并随机产生20个阈值,然后进行分裂,看看哪一对点分裂的结果方差最小,就将其作为分裂的依据。
下面几个图是实验结果


免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删