一个完整的ALE过程可以分为若干个网格remesh子过程,而每一次remesh的过程可以分为两步:生成新网格(create a new mesh)→环境变量转换(advection variales)。
Create a new mesh:
利用各种算法以及控制策略生成一个良好的网格
Advection variales:
也就是将旧网格中的变量信息利用remapping技术转换到新网格中,也有不同算法,其中包括静变量(应力场,应变场等)的转换与动变量(速度场,加速度场等)的转换
简单来说就是,造新房子(create a new mesh),把旧房子里的家具搬过来(advection variales)。
生成的新网格成功与否则在于对这两步的控制

在step功能模块,上方的菜单栏other中可以找到ALE相关设置
主要有下面几个子选项:
ALE Adaptive Mesh Domain
ALE Adaptive Mesh Constraint
ALE Adaptve Mesh Controls
Seneral Solution Controls
Solver Controls
分别是
ALE自适应网域
ALE自适应网格约束
ALE自适应网格控制
一般求解控制
求解器控制
对于如何设置参数,将按照顺序从以下几个部分一点点描述:
上文说到:每一次remesh的过程可以分为两步:生成新网格(create a new mesh)→环境变量转换(advection variales)。即造新房→搬家具
这一部分考虑的就是:怎么造新房,怎么搬家具
在ABAQUS中是如何生成新网格的呢?
即使用网格扫掠技术(mesh sweep technique),每sweep一次,生成一套新的网格。但是当你使用的算法不同时,sweep出来的网格也是不同的,打个不是很恰当的比方:用不同的工具做同一件东西,做出来的质量与精度会不一样,同样,用不同的算法来sweep网格,得到的网格质量也会不一样。
在ABAQUS显式模块中,sweep算法用英语来说就是mesh smoothing method,有三种算法来sweep网格,如下所示:
1)体积算法(volume smoothing)
该算法十分健壮,为默认算法,在绝大多数情况下适用
2)拉普拉斯算法(laplacian smoothing)
耗费资源最少的算法,能力一般,作用与体积算法类似(一阶算法,类似于求平均值),对于曲率比较高的曲线曲面边界时,效果不是很理想
3)等位算法(equipotential smoothing)
比较复杂的算法,是基于拉普拉斯算法的解之上的算法,对曲率较大的曲线曲面边界效果较好,在节点被非结构化网格包围时,此算法为推荐算法,若节点被结构化网格包围,其效果与体积算法类似。
三种算法可以结合适用,利用权重值来定义,需要记住的是,三种算法各占的权值加起来必须等于1。step功能模块中,在Other→ALE Adaptve Mesh Controls→Create→Continue可以看到下图

三种算法权值设置选项卡
在ABAQUS中是如何将旧网格中的环境变量转换到新网格中的呢?
即使用remapping技术,对于静变量(应力场,应变场,位移场等)的转换(advection),有两种算法即为一阶算法(first order)与二阶算法(second order)算法,second order算法适用于所有问题,为推荐算法,一阶算法比较简单,占资源少,速度快
对于动变量(速度,加速度等)转换(momentum advection),也有两种算法,element center projection method与half-index shift method,前者为推荐算法,选择前者就ok了,如果想仔细研究,查查ABAqus文档就可以了,里面写的很清楚。
step功能模块中,在Other→ALE Adaptve Mesh Controls→Create→Continue可以看到下图

变量转换算法
这一部分考虑的就是:多久造一次新房,什么时候搬完家具
这就涉及到以下几个参数。
(1)Frequency控制(频率控制)
主要是对整个step time中网格remesh的次数进行控制。
Remesh次数n 可以由 n = Increment number /Frequency 来表达其意义,当frequency的值为 i 时,表示每 i 个增量步进行一次remesh。
**一个典型的ALE过程,在每5-100个增量步就需要一次remesh。
**对于拉格朗日问题,改参数默认值为10,若变形实在太大,可适当调高,以增加网格重画的强度
**对于爆炸,碰撞等变形时间极短的问题求解,则在每一个增量步都需要一次remesh,这时Frequency的值需要设置得很小,比如设为1,当然,adaptive remesh过程的强度也很高,也会很废时。
**对于其他变形不是很剧烈的问题求解,该参数值可以适当调高。
**对于欧拉问题,默认值为1。
(2)Mesh Sweeps参数控制
我们先来理解一下sweep的概念,每sweep一次,abaqus将利用我们设置好的算法(体积算法,拉普拉斯算法或等位算法)生成一套新的网格,但这个网格不一定是符合要求的,因此,需要在生成的新网格的基础上用同样的方式再进行sweep,就像我们求解方程时迭代的概念是一样的。
就这样一直sweep下去直到sweep的次数达到mesh sweeps参数的值,这样就完成了一个remesh过程中的新网格的生成。
同样,mesh sweeps参数的值越高,adaptive remesh过程强度越高,网格优化的状况良好的机率也就越大。
当该参数的值为 n 时,每一个remesh过程将对网格进行 n 次sweep,其实这个参数可以理解为对整个adaptive remesh过程的每一个子过程(remesh过程)的强度进行控制。
step功能模块中,在Other→ALE Adaptve Mesh Domain→Manager→Edit 可以看到下图
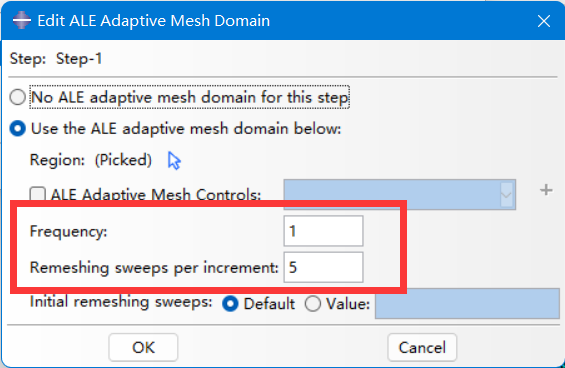
“强度控制”
也就是ALE过程开始之前对网格的一个优化,概念与mesh sweeps类似,因为我们有可能利用已经变形的很厉害的网格进行分析,这时,在分析开始之前,就需要对网格进行重画。
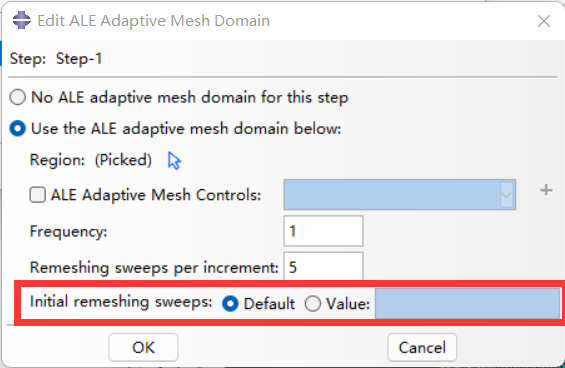
intinal remeshing sweeps
也就是指网格梯度控制(是否保持初始网格梯度,若需要保持初始网格梯度,则对网格的质量将会有影响)。
对于拉格朗日问题选择Improve aspect ratio,在计算过程中将考虑到网格单元高宽比的改善,不考虑对初始网格梯度的保持。
对于欧拉问题选择:Preserve initial mesh grading,在计算过程中保证初始的网格梯度,但不会考虑到网格宽高比的改善。
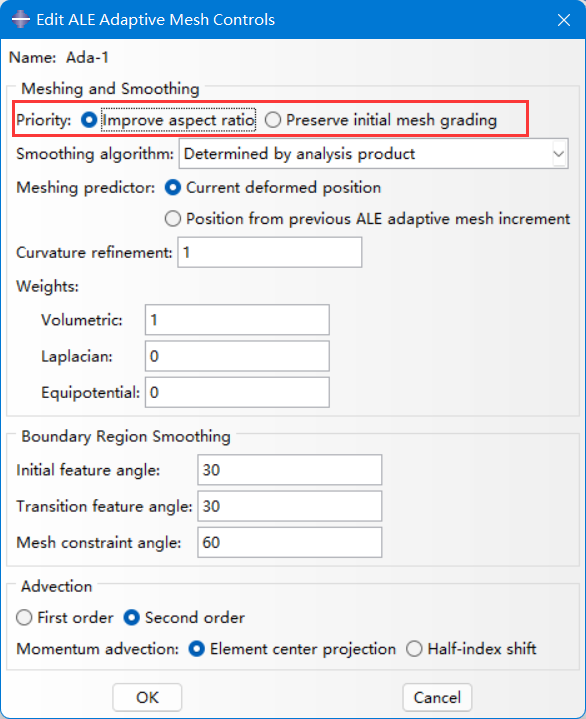
(2) priority参数设置
选项:Use enhanced algorithm based on evolving element geometry
主要是在几何学的方面对我们定义的网格sweep算法(前面提到的三种算法)进行增强,目的是为了保证adaptive remesh过程的健壮性,为推荐选项,选它就行了
选项:conventional smoothing
利用我们定义好的算法进行计算,无几何增强。
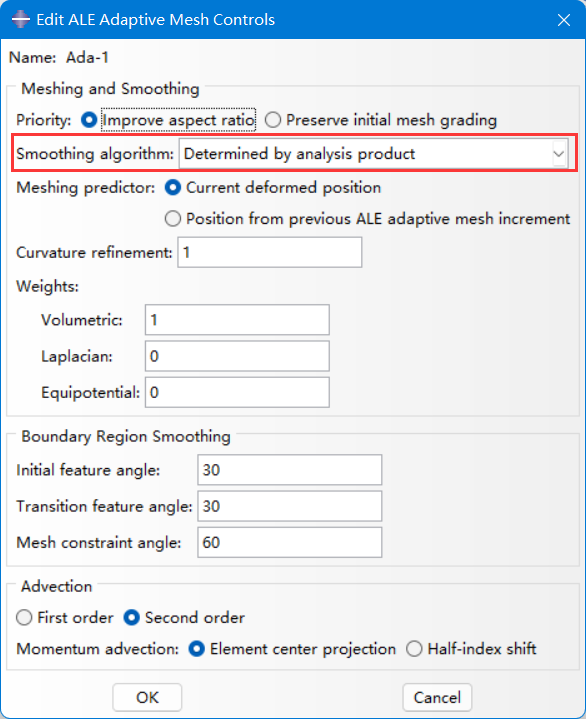
smoothing algorithm 参数设置
也就是网格节点位置控制(理想的网格节点位置控制,将会减少需要的网格sweeps次数,减少资源浪费)
对于拉格朗日问题选择Current deformed position,
对于欧拉问题选择Position from previous adaptive mesh increment
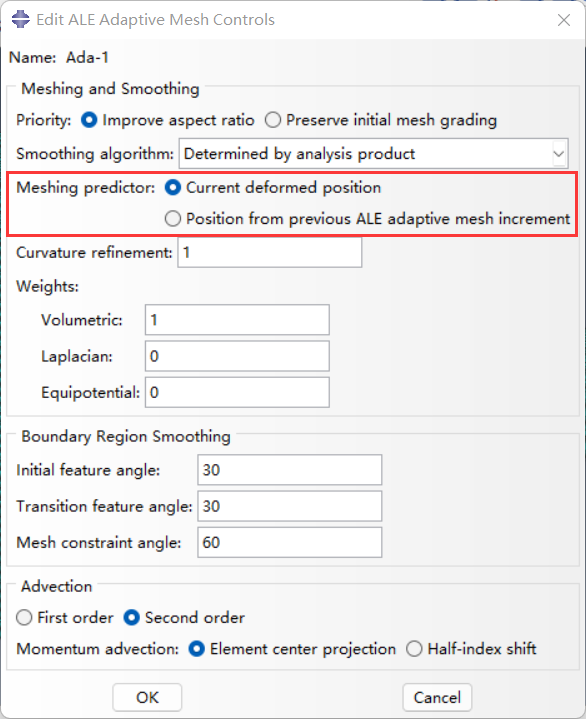
Meshing predictor参数设置
3.5 Curvature refinement参数设置
也就是曲率较大的曲线曲面边界的网格密度控制,默认为1,该值越大,则圆角区
的网格密度也就会越大
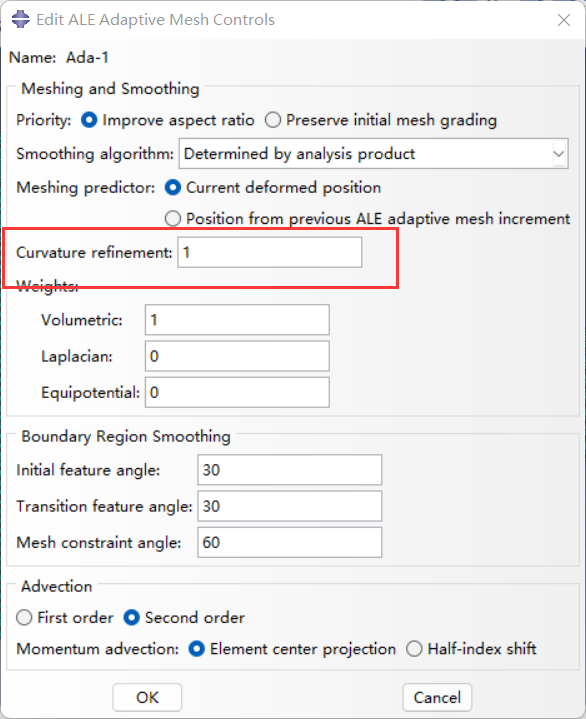
Curvature refinement参数设置
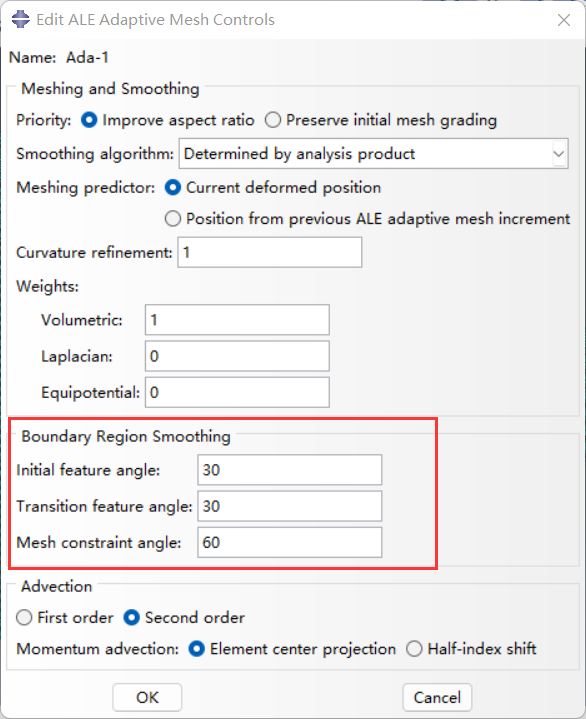
boundary region smoothing
(1) initial feature angle
即初始检测角度的设置,当两个相邻的面的法向量大于该角度值的时候,这两个相邻面形成的corner将被检测出来,在sweep时,网格不允许通过这个corner
小于的话就说明,该corner足够圆滑,网格可以通过,当然,该corner应该是具有活性的,对corner活性的控制由下面一个参数(Transition feature angle)控制,否则也不会被考虑。
(2) Transition feature angle
控制被检测出的corner的活性的,如果被检测处的corner的两面法线夹角大于该值则该corner在ale过程中是会被考虑的,否则就不会考虑。
(3) Mesh constraint angle
控制分析过程的一个角度参数,一般大于45度,设为默认值就可以,在分析过程中,当网格内某一个角度大于该参数值时,分析终止
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删