Abaqus/Standard应用Newton-Raphson算法解决非线性问题，木木本期就为同学们“尽可能”全面讲解该算法，从Abaqus内部算法到数学问题中的非线性方程Newton-Raphson算法理论，最后结合具体非线性方程给出相应的代码，如此一来，更加生动地演绎Newton-Raphson迭代过程。

Abaqusd的Newton-Raphson算法

在Abaqus隐式求解时，将载荷划分为一定数量的增量步(increments)施加于结构，每个增量步结束时寻求近似平衡解，若干次迭代后才能获得最终平衡解。Abaqus/Standard组合了上述增量和迭代过程。

Abaqus/Explicit中，默认情况下时间增量步大小完全是自动选取。在求解非线性问题时，不需要形成切线刚度矩阵，需要的是一个小小的增量步，只依赖与模型的高阶自振频率，与载荷类型和加载时间无关，无需迭代即可获得解答。

增量步和迭代步：

Abaqus/Standard可以让用户指定初始增量步大小，后继计算过程中系统会自动选择增量步的大小，在每个增量步结束时，结构处于近似的平衡状态，将计算结果，写入到.odb文件中。

平衡迭代和收敛：

在第一个增量步载荷中，Abaqus/Standard基于结构的初始构形和结构初始刚度和计算关于结构的位移修正值，基于将结构的构形更新为。

在更新后的构形，形成新的切线刚度，进而计算新的内部作用力，总载荷与内部作用力差值记为残差力：

线性问题中，残差力在模型每个自由度上均为 0 ，结构处于平衡状态。在非线性问题中，Abaqus/Standard将残差力与设定的容许值（容许残差）进行比较，若小于容许残差值，则就是结构在所施加载荷下有效的平衡构形，除此之外，Abaqus/Standard还要检查位移修正值是否相对于总的增量位移很小。若大于增量位移的,将进行下一次迭代。上述两个条件都满足后，才认为结果是收敛的。

默认的容许值在整个时间段上作用与结构上的平均力的。在整个模拟过程中，Abaqus/Standard会自动地计算平均力。

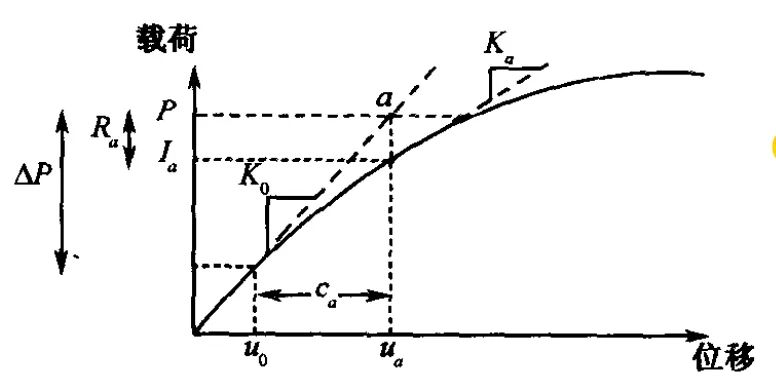
   图 1：在一个增量步中的首次迭代(源自《ABAQUS非线性有限元分析实例》庄茁 P192)
 

Newton-Raphson（N-R）迭代法的原理

Newton-Raphson（N-R）迭代法主要以分步逼近的方法计算，在每一增量步中，采用已得到的位移值带入并求得与位移有关的切线刚度矩阵的值，再进行线性计算，反复调整计算的载荷值与设定载荷值的差进行迭代，使其达到设定的精度。

主要步骤

Step 1：将总外载荷$\bar{P}$分为一系列的载荷段，

Step 2：在每个载荷段中进行循环迭代，直到在该载荷段内收敛。 每个迭代步中刚度方程为： 式中的表示第个载荷步。

Step 3：将所有载荷段循环迭代，并将结果累加。

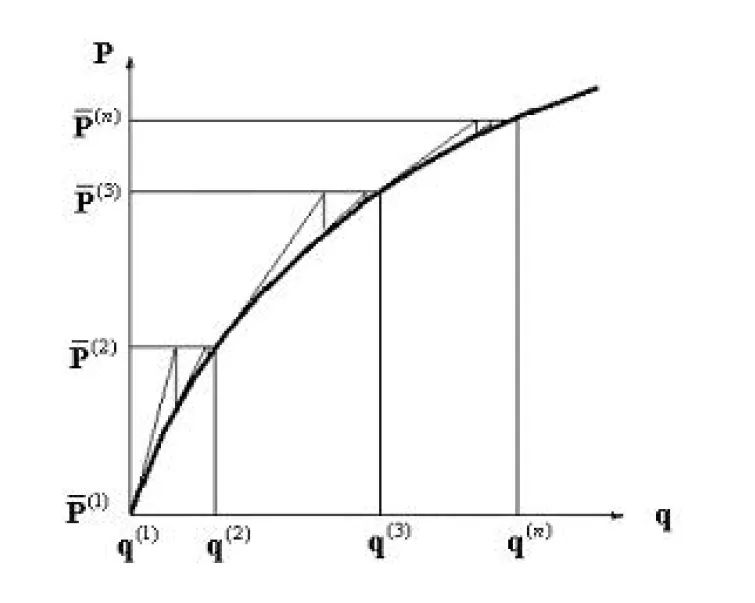
   图 2：增量步循环迭代示意图
 

缺点：Newton-Raphson（N-R）迭代需要每次形成切线刚度矩阵，带来比较大的计算量，这也是隐式分析相对于显示分析计算时间大大增加的重要原因。

修正方法：在自己非线性有限元编程时，可以将上述迭代过程稍加修正，将每次迭代时的切线刚度矩阵换做初始切线刚度矩阵，并且在迭代时保持不变，即可大大减少计算量，修正方法如下图所示：

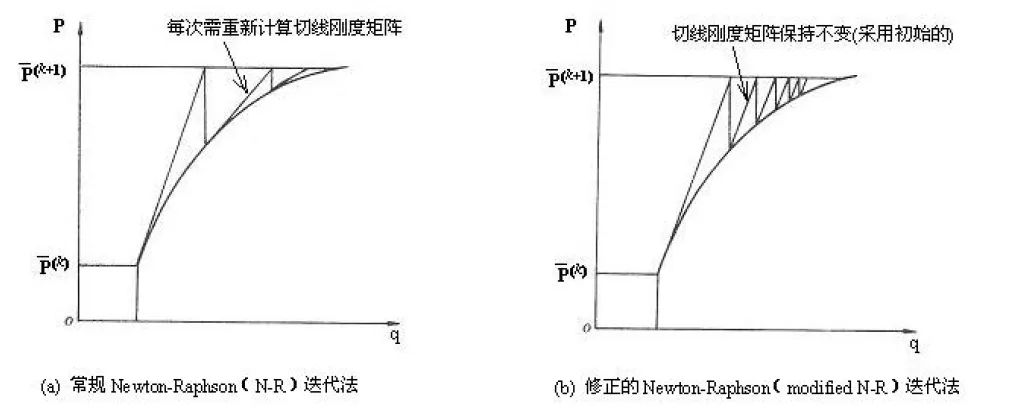
   图 3：Newton-Raphson（N-R）迭代法与修正的 Newton-Raphson（N-R）迭代法
 

求解非线性方程的Newton-Raphson算法

数学解释

非线性方程的根记为 ，按照牛顿迭代法：

牛顿迭代计算流程：

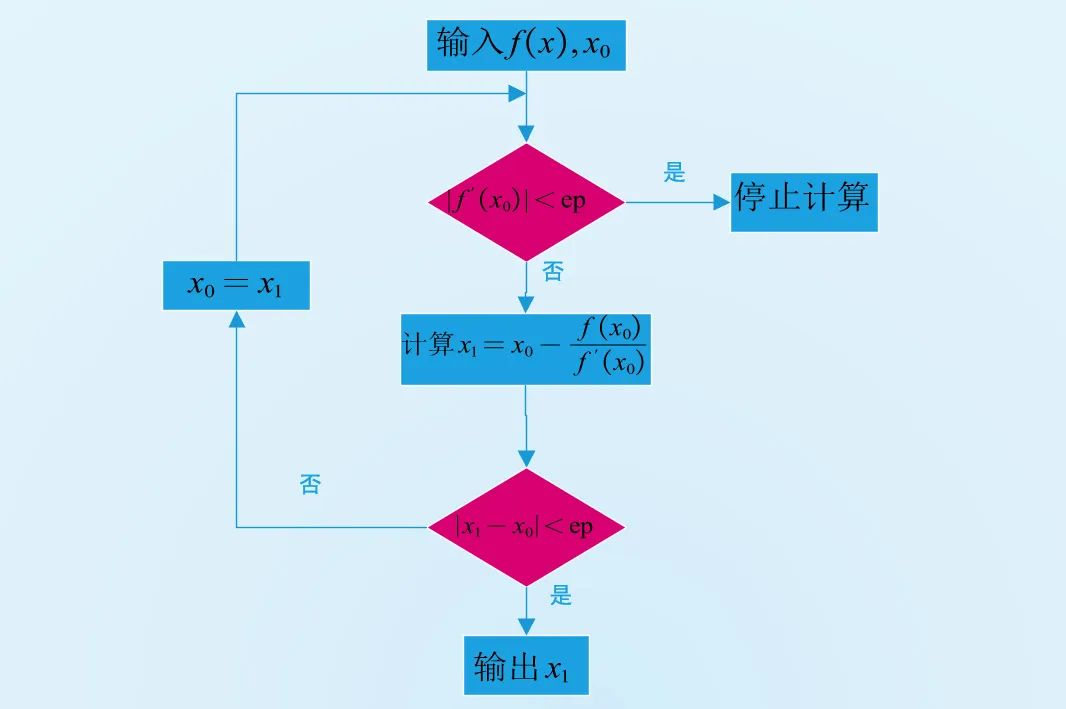
   图 4：牛顿迭代法计算流程
 

Newton-Raphson迭代算法：

function varargout=newton(fun,x0,ep,maxiter)
% NEWTON  牛顿法求方程的根
if nargin<4
    maxiter=500;  % 默认最大迭代次数
end
if nargin<3
    ep=1e-8;  % 默认允许误差
end
if ~isscalar(fun)
    dfun=fun{2};  % 导函数匿名函数形式
    fun=fun{1};  % 函数的匿名函数形式
else
    if isa(fun,'sym')  % 函数以符号表达式的形式给出
        dfun=matlabFunction(diff(fun));  % 导函数匿名函数形式
        fun=matlabFunction(fun);  % 函数的匿名函数形式
    elseif isa(fun,'function_handle')  % 函数以匿名函数或函数句柄的形式给出
        dfun=matlabFunction(diff(sym(@(x)fun(x))));  % 导函数匿名函数形式
    end
end
iter=1;  % 迭代次数
xs(iter,1)=x0;  % 迭代序列初始值
exitflag=1;  % 迭代发散标志，1表示迭代收敛，0表示迭代发散
x1=nan;  % 预置x1的初值
while exitflag
    fx=fun(x0);  % 计算x0处的函数值
    dfx=dfun(x0);  % 计算x0处的导数值
    if abs(dfx)<=eps || iter>maxiter  % 若导数为0或迭代次数大于最大迭代次数
        exitflag=0;  % 认为迭代发散，即根不可靠
        break  % 退出循环
    end
    x1=x0-fx/dfx;  % 牛顿迭代计算
    xs(iter+1,1)=x1;  % 将迭代值依次存入迭代序列中
    if abs(x1-x0)<=ep  % 前后两次迭代值差的绝对值在允许的误差范围内
        break  % 跳出循环
    end
    x0=x1;  % 更新迭代初始值
    iter=iter+1;  % 迭代次数累加
end
[varargout{1:5}]=deal(x1,...  % 第一个输出参数为函数零点
    fun(x1),...  % 第二个输出参数为零点处的函数值及导数值
    exitflag,...  % 第三个输出参数为迭代收敛标志
    iter,...  % 第四个输出参数为迭代次数
    xs);  % 第五个输出参数为迭代序列

实例详解

例：利用Newton-Raphson算法求解函数在 3.8 附近的零点。

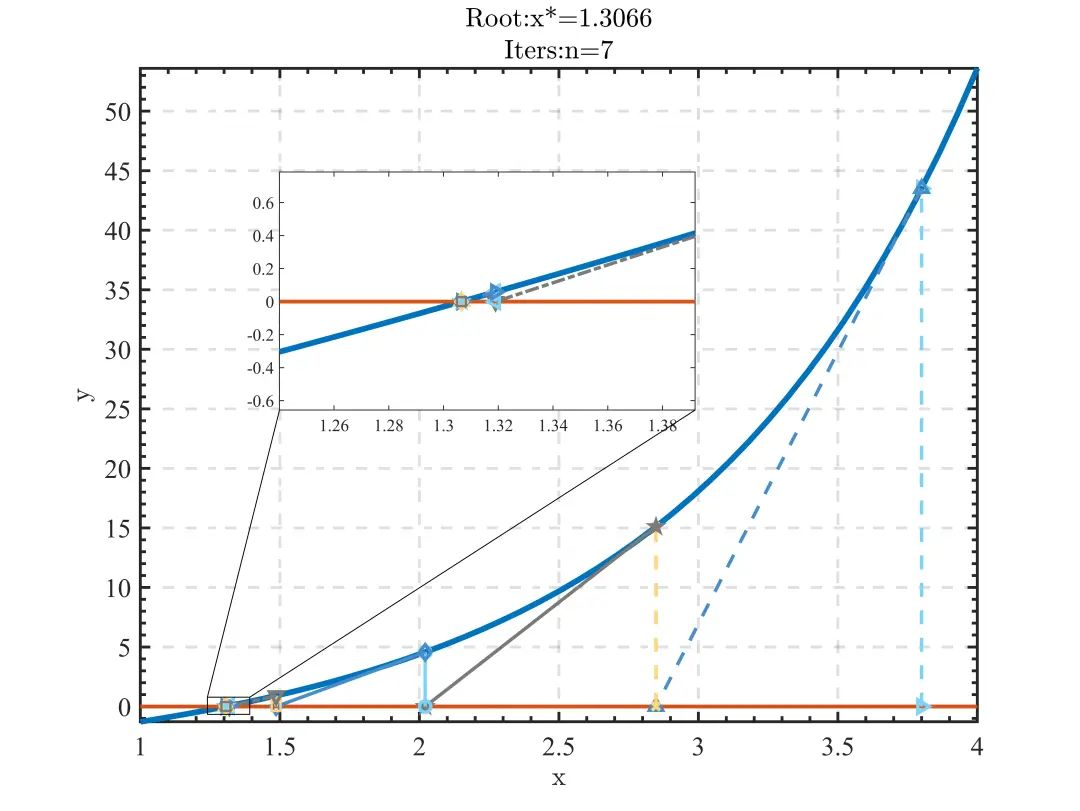
   图 5：非线性迭代求解

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删