非线性求解案例及Abaqus应用

非线性问题求解的判据为内部作用力I和外部作用力P必须互相平衡。作用于一节点的内部作用力是包含此节点的各单元中的应力引起的，如下图所示。结点I上的作用力是其周围四个单元力Ia，Ib，Ic，Id 的合力。

ABAQUS使用Newton-Raphson法求解非线性问题，线性问题只用一组方程就可求解，而非线性问题则是逐步施加载荷，以增量形式无限趋近最终解。在进行非线性问题求解时，将过程分为多个载荷增量步，在求解增量步的同时可能需要若干次的迭代才能求得载荷增量步最优解，将所有的载荷增量步加起来可得非线性分析的近似解。

非线性问题分析过程主要有三个“步”：分析步，增量步和迭代步。

分析步：仿真计算过程包括单个或者多个步骤。它包括分析步类型选择，载荷选择及输出要求选择。而且对于复杂的变形过程建立多个分析步，每个分析步都可以有不同载荷、边界条件、分析过程和输出要求。

增量步：是分析步中的一部分。在非线性分析过程中，一个分析步往往被分解为多个小增量步。在确定初始增量步大小后，ABAQUS会自动选择后边的增量大小，结构在每个增量步结束时都处于平衡状态。计算结果会写入输出数据库文件、重启动文件、数据文件及结果文件中，选择某一增量步的计算结果写入的数据称为帧。

迭代步：是在增量步中找到平衡解的一种尝试。如果模型在一次迭代结束没有达到平衡状态，ABAQUS将进行另一轮迭代。随着迭代次数的增加，ABAQUS求得的解会越来越接近平衡状态。只有得到了一个平衡解，一个增量步才能完成。

非线性问题的求解有两个重要的概念：平衡迭代和收敛性。

平衡迭代：结构对于一个小的载荷增量的▲P的首次迭代过程如下图所示。

ABAQUS利用基于U0时结构的初始刚度为K0和增量▲P来计算结构的位移修正值Ca，利用Ca将结构的构型更新为Ua。

收敛性：基于结构新的构型Ua，ABAQUS形成新的刚度Ka，利用Ka来计算更新后的结构中内部作用力Ia。所施加的总载荷P和Ia的差值如下计算：Ra=P-Ia。其中Ra是迭代的作用力残差值。若Ra在模型的每一个自由度上均为零则上图的a点将位于载荷—位移曲线上，结构处于平衡状态。如果Ra比作用力容许残差小，ABAQUS就接受结构的更新构型作为平衡结构。若迭代结果不收敛，则ABAQUS将进行另一种迭代以使内部和外部作用力达到平衡。如下图所示：

第二次迭代是利用了第一次的迭代结果Ka和Ra一起来确定另一位移修正值Cb，这使得系统更加接近平衡状态。同样的，ABAQUS利用结构新构型Ub内部作用力计算更新新的作用力残差值Rb，再次将任意自由度的最大作用力残值与作用力残差容许值进行比较，将第二种迭代的位移修正值Cb与增量位移∆Ub=Ub-U0进行比较，若∆Ub/Cb的比值小于1%，则满足收敛条件。如果还没收敛，则进行下一次迭代。

自动增量控制：ABAQUS能够自动调整载荷增量步的大小，用户只用在每个分析步计算中给初始增量步的大小，ABAQUS会自动调整后续增量的大小。如果用户没有设定初始增量步的大小，ABAQUS会将分析步的全部载荷作为第一个增量步载荷来施加。若是分析高度非线性问题，ABAQUS将不得不多次减小增量步的大小，这会极大的浪费计算时间。

在一个载荷增量步中得到收敛解所需要的迭代步数会随着系统的非线性程度而变化。ABAQUS默认情况下，在迭代16次仍然不收敛，ABAQUS就会放弃当前的增量步，将增量步减小25%后重新计算，若仍不收敛，ABAQUS会继续减小增量步，在迭代5次都不能得到收敛解的情况下，就会终止计算。若增量步的解在少于5次迭代就收敛，并且连续两次增量步的求解都少于5次，ABAQUS会自动将增量步大小提高50%。

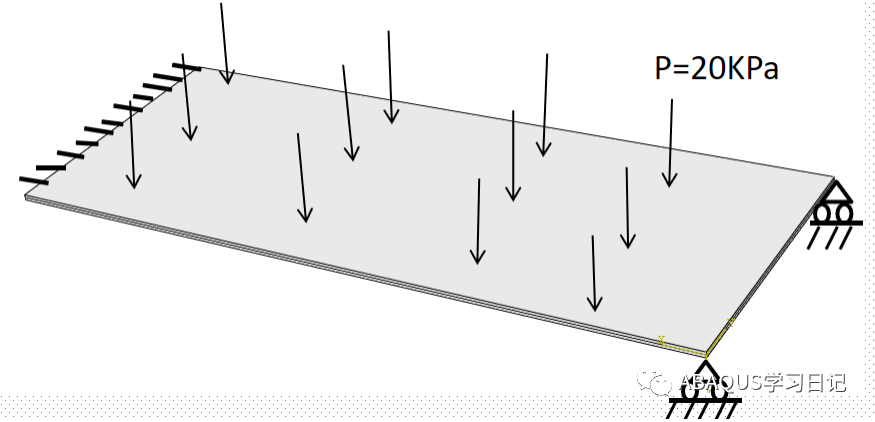
下面以一个实例计算过程来说明这几种概念。模拟一个如图所示的平板其长1m,宽0.4m，厚0.008m，该板一端固定，另一端只能沿平行于平板的轴向移动，受均布载荷P=20KN。弹性模量E=30e9,泊松比u=0.3。

1.建立Part。创建一个三维的壳，模型大约尺寸设定维4（采用m为单位）。

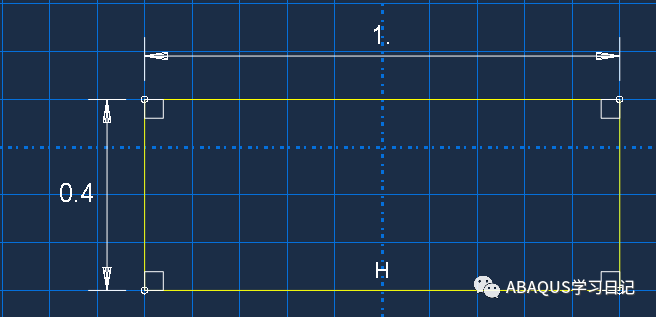
绘制草图如下：

2.建立材料属性Property。

建立壳截面属性，其厚度为0.008m。

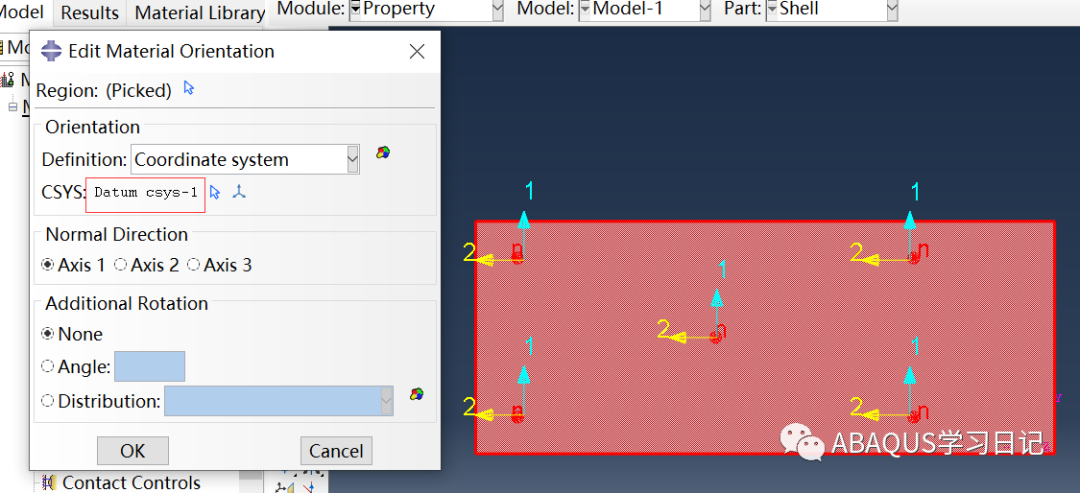
壳单元与实体单元是不一样的，每个壳单元都有局部材料方向。用户能够使用局部直角坐标系、柱坐标系和球坐标系代替整体的笛卡尔坐标系。创建了局部坐标系后，要使局部坐标系的坐标轴方向与材料方向一致。建立局部坐标系如下图，在壳的右下角创建了一个直角局部坐标系。

给壳赋予方向:Assign→Material Orientation，接着选中整个Shell，然后将新建的坐标系赋予Shell。

3.装配。

4.创建载荷分析步。载荷步类型选择Static、General，初始增量步设为0.1。由于总时间为1，所以abaqus在第一个增量步中施加载荷的大小为总载荷的10%。

5.设置边界条件及施加载荷。部件左端全部固定，右端只保持U1的自由度，其他方向的自由度全部被固定。边界条件的设置如下图所示：

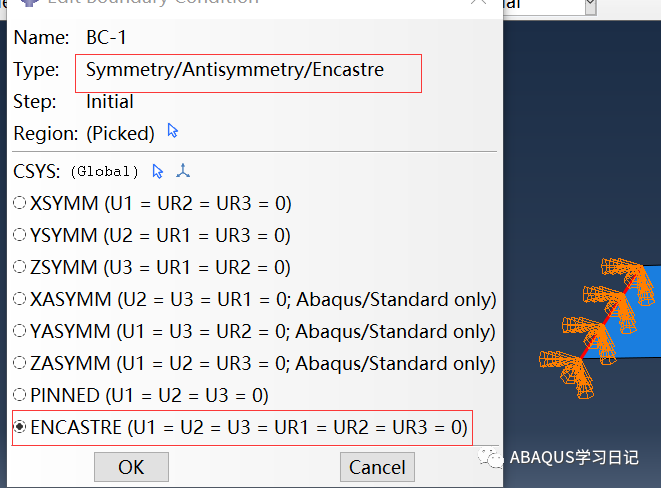
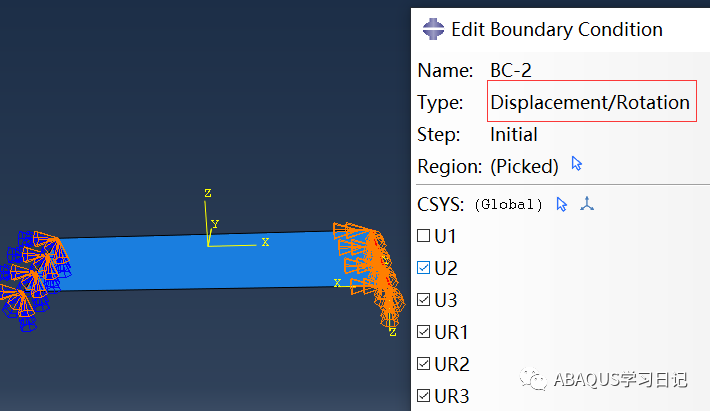
接着施加载荷，载荷为类型为Pressure,大小为20000N。

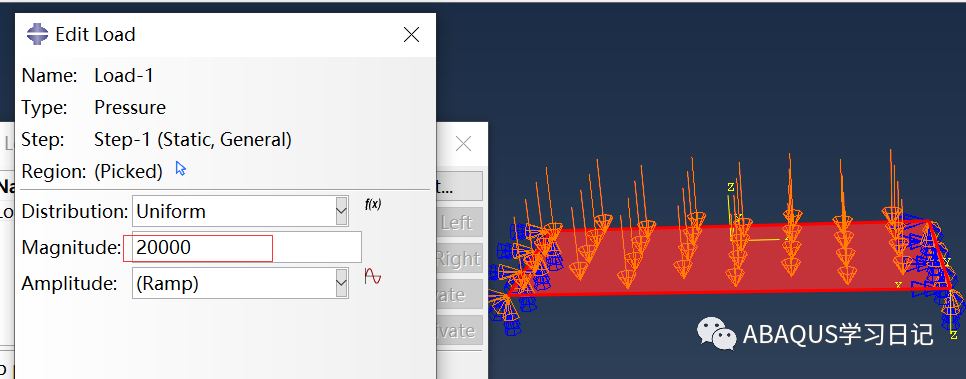
6.网格划分。

因为部件属性是三维的壳，选择单元类型为S8R。

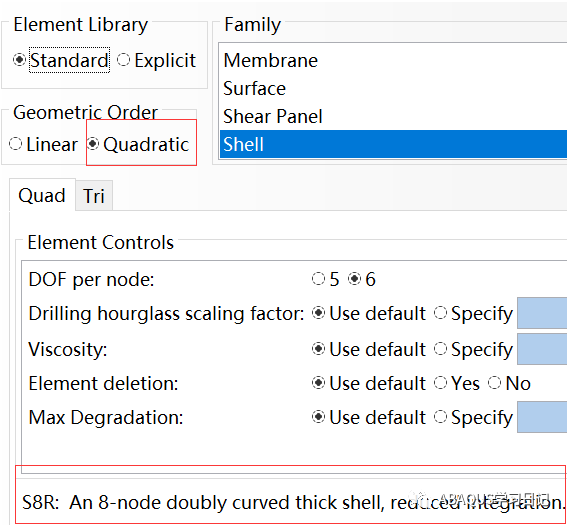
计算的应力如下图所示：

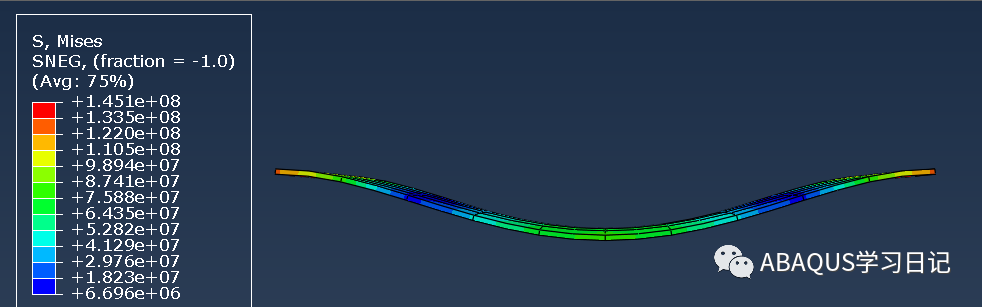
计算结束后，打开Job Monitor,可以查看分析步、增量步、迭代次数、分析步时间、时间步增量的大小。

分析该图可以知道，ABAQUS是如何控制载荷在每个分析步中的比例。在初始增量步和第二个增量步中，增量步时间为0.1，且都是只需要1步迭代就可以收敛。在连续两次迭代次数少于5次的情况下，ABAQUS会自动把下一个增量步加50%，故第三个增量步的计算时间为0.15。同理也增加第四个和第五个增量。

另外，ABAQUS会输出很多计算文件，其中msg信息文件包含了很多分析过程中的详细情况。在该文件中不仅列出了容许残差和控制参数，还给出了每一次迭代的概要说名。并且给出了最大的残余应力rαmax，最大位移量∆Ua，最大位移修正量Ca,时间平均力qa,同时也给出了rαmax,∆Ua，Ca的节点和自由度。下图为本例的msg文件中关于第一个增量步的迭代信息。

由msg文件中的信息可知，时间平均力qa为0.426，最大残余应力为8.544E-10，远小于0.005×

qa，满足迭代条件。同时还要检查位移修正值是否满足平衡条件。在首次迭代中，最大位移增量∆Ua与最大位移Ca总是相等的，不满足平衡条件∆Ua/Ca<1%，但该准则不是绝对的，如果ABAQUS判断结果为线性的，该准则就会被忽略，上图红框内的内容说明是线性的增量，因此位移修正值也满足平衡条件。针对壳单元，ABAQUS还需要检查力矩是否平衡，其结果也是满足平衡条件的。所有的平衡准则都满足，就完成了一个增量步的计算。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删