有限元案例分享：结构非线性仿真不收敛的解决策略

主要通过分析一个扬声器Kms(x)仿真不收敛的解决案例，来讨论下有限元非线性计算时应该注意的事项，以及非线性计算时求解器设置。供各位参考。

昨天一个朋友用comsol分析一款支片（弹波）的Kms（x）时，用最大位移5mm计算时，收到一个错误提示：“达到最大牛顿迭代次数”。只能计算到2mm。我花了点时间帮助他解决了一下。就以此为案例，解剖下麻雀。

Comsol复杂模型的默认网格划分/默认求解能力和非线性的计算能力相比较与其他软件如Ansys或者ABAQUS是存在一定差距的，所以网格和求解器在求解复杂非线性模型时需要根据有限元计算理论进行一定的手动调整。

首先介绍下，Kms(x)的仿真分析大致有两种思路：1.给定一个力，然后计算位移，力/位移就是Kms。2.给定一个位移，然后计算其他刚性部件的反作用力，力/位移就是Kms。这两种思路对应的有限元软件内部算法也略有差异，不过一般使用专业软件不需要考虑那么深。

以下讨论的解决技巧不局限于comsol,对其他软件进行非线性仿真时出现不收敛也是适用的。

我的解决思路是这样的：

1.   检查结果。支片在2mm时显然未拉伸至最大，所以不是因为变形过大造成不收敛。

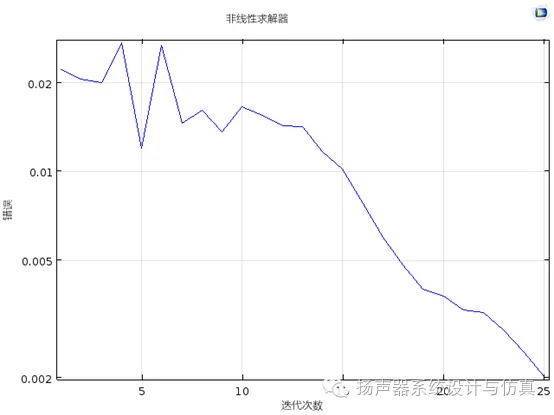
2.   检查求解记录。通过查看求解器的收敛曲线，发现未相对误差经过25次迭代之后未达到0.001，从而显示不收敛。

3.   检查参数。这个案例用的是给定一个位移，然后计算反作用力的方法。Comsol采用参数化扫描时，需要避开位移0点，否则Kms计算会出错。所以位移设置修改为从-5.01mm计算到5mm。

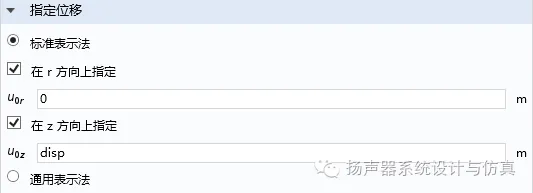
4.   检查物理场边界/载荷设置。加载位移时，除需要计算方向指定位移外，将其他方向的位移设置为0。防止计算误差导致在理论上不可能有位移的方向移动。

5.   检查网格。网格足够密。适当调稀疏了点，够用就好。

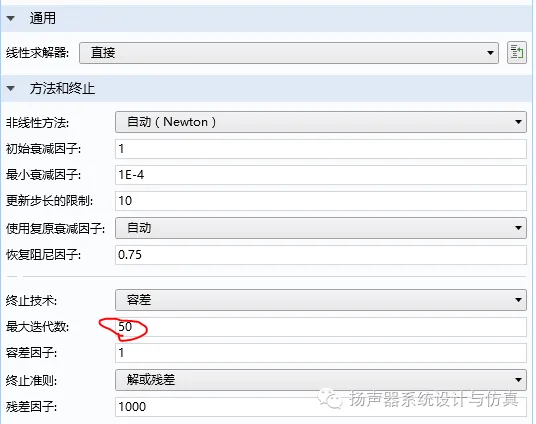
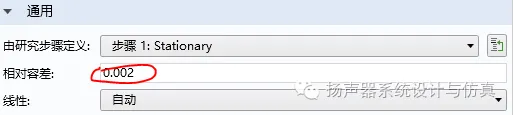
6.   检查求解器设置。这是这个案例最关键的部分。首先将最大迭代数从默认25修改为50，发现相对误差还是大于0.001。所以再考虑将相对容差从默认0.001调整为0.002，当然这个会损失一定的精度。具体见下面的图。

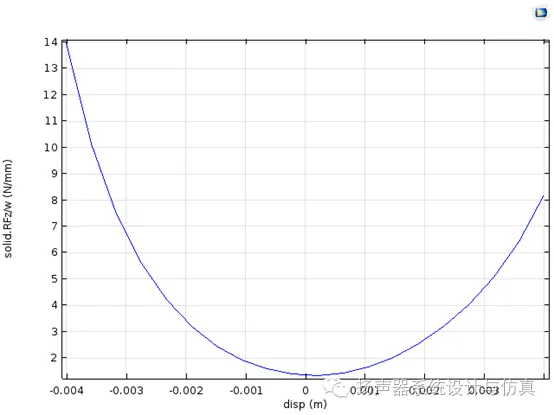
7.   顺利求解完成。从结果来看，精度的损失是可以接收的，Kms(x)曲线光滑且走势符合预期。当然其中经过多次参数尝试和调整。不过大体思路就是这样。遇到类似问题的朋友也可以照此解决。

最后，以comsol的结构非线性求解为例，大体讲解下求解器的相关设置。有兴趣的可以按下F1多看看官方的帮助文档，这个是最专业的。

默认采用的是直接求解法，存在多个求解器。直接法一般是通过牛顿迭代法，转化为线性问题，然后直接暴力展开矩阵求解。这种方法比较稳定，鲁棒性强，不过内存占用较多。

也可以修改为迭代求解，同样存在多个求解器。相对直接求解，可以减少内存开销，计算速度一般情况下会略快。不过相对更容易不收敛，不如直接法稳定。需要一个比较好的初始预估值，不然结果容易发散。

考虑不同非线性程度，可以考虑不同的非线性方法。默认就是定常的牛顿法。形状畸变比较严重的结构，需要考虑使用比如自动高度非线性牛顿法。遇到不收敛的情况，有时也需要适当调整阻尼因子，以增加收敛性和鲁棒性。

通常情况下非线性不收敛可以参考本案例，检查好参数/物理场设置/网格/求解器即可。求解器优先选用默认的直接法求解，遇到问题优先调整迭代次数，还有问题再调整相对容差，最后再考虑更换求解方式或者调整其他参数。当然具体需要结合收敛曲线分析判断。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删