Abaqus-Umat线性随动强化子程序验证方法

模型描述：假设某种材料，弹性模量E=200GPa，泊松比u=0.3，线性强化特性如下曲线所示，在一个直径d=10mm，长度L0=50mm的试样的一端约束Z向和周向变形（不约束断面的径向，这样可更好的模拟拉伸实验），另一端先施加509Mpa的轴向拉力，然后在反向施加509MPa的轴向压力。

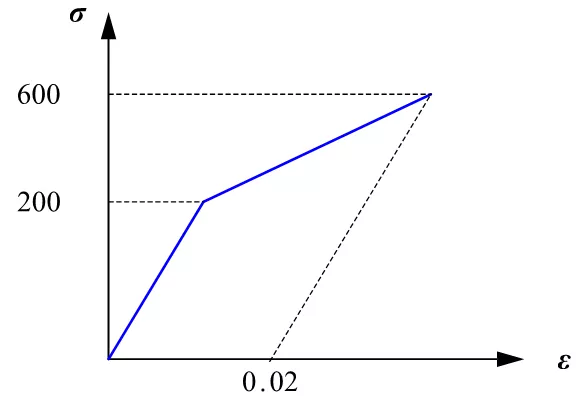
详细的模型操作和代码文件可在公众号内回复：线性随动。即可自动获取。

  部分Umat如下：

SMISES=(STRESS(1)-ALPHA(1)-STRESS(2)+ALPHA(2))**2
     1  +(STRESS(2)-ALPHA(2)-STRESS(3)+ALPHA(3))**2
     1  +(STRESS(3)-ALPHA(3)-STRESS(1)+ALPHA(1))**2
        do K1=NDI+1,NTENS
            SMISES=SMISES+SIX*(STRESS(K1)-ALPHA(K1))**2
        enddo
        SMISES=SQRT(SMISES/TWO)
C
C GET YIELD STRESS AND HARDENING MODULUS
C
        SYIELD=PROPS(3)
        HARD=PROPS(4)
C
C DETERMINE IF ACTIVELY YIELDING
C
        if(SMISES.gt.(ONE+TOLER)*SYIELD) then

C
C ACTIVELY YIELDING
C SEPARATE THE HYDROSTATIC FROM THE DEVIATORIC STRESS
C CALCULATE THE FLOW DIRECTION
C
            SHYDRO=(STRESS(1)+STRESS(2)+STRESS(3))/THREE
            do K1=1,NDI
                flow(K1)=(STRESS(K1)-SHYDRO-ALPHA(K1))/SMISES
            enddo
            do K1=NDI+1,NTENS
                flow(K1)=(STRESS(K1)-ALPHA(K1))/SMISES
            enddo
C
C SOLVE FOR EQUIVALENT PLASTIC STRAIN INCREMENT
C
            DEQPL=(SMISES-SYIELD)/(HARD+EG3)
C
C UPDATE SHIFT TENSOR, ELASTIC AND PLASTIC STRAINS AND STRESS
C
            do k1=1,NDI
                ALPHA(K1)=ALPHA(K1)+HARD*flow(K1)*DEQPL
                EPLAS(K1)=EPLAS(K1)+THREE/Two*flow(K1)*DEQPL
                EELAS(K1)=EELAS(K1)-THREE/Two*flow(K1)*DEQPL
                STRESS(k1)=ALPHA(k1)+FLOW(k1)*SYIELD+SHYDRO
            enddo
            DO k1=NDI+1,NTENS
                ALPHA(K1)=ALPHA(K1)+HARD*flow(K1)*DEQPL
                EPLAS(K1)=EPLAS(K1)+THREE*flow(K1)*DEQPL
                EELAS(K1)=EELAS(K1)-THREE*flow(K1)*DEQPL
                STRESS(k1)=ALPHA(k1)+FLOW(k1)*SYIELD
            ENDDO

Mises应力云图动画如下图：

应力-应变关系图如下：

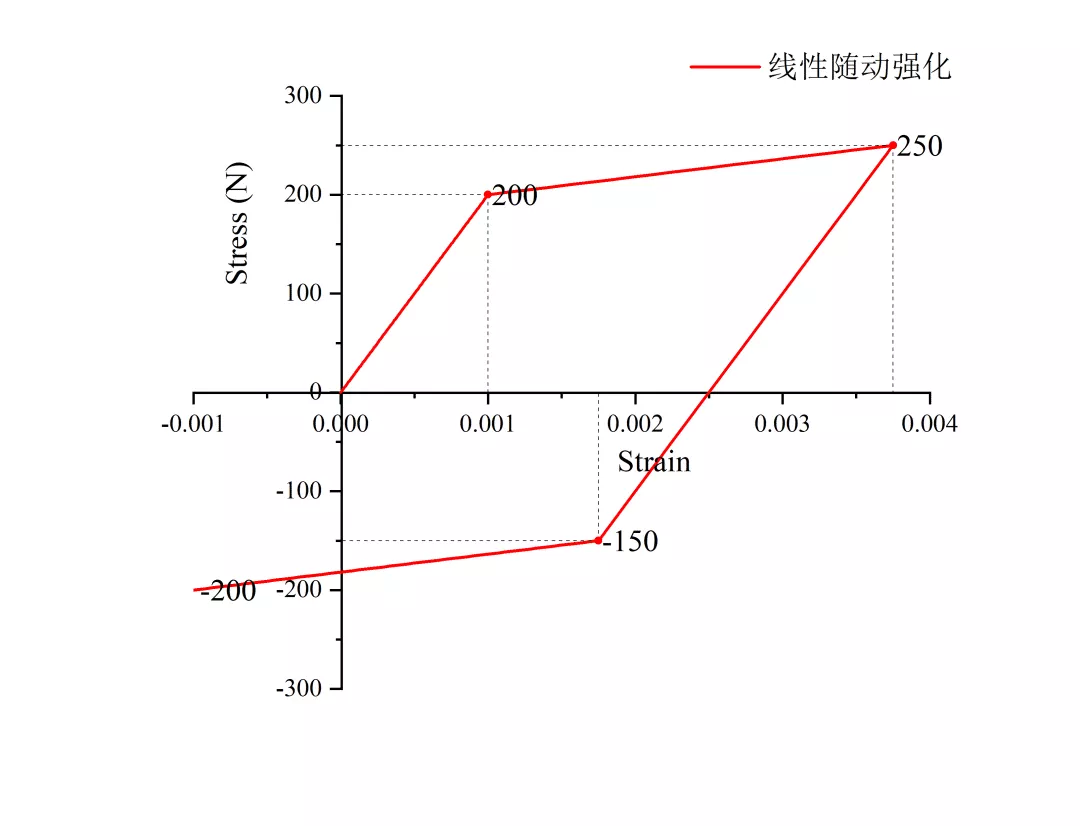
从图中可以看到后继屈服压缩应力满足线性随动强化法则，同时体现出理想的Bauschinger(包辛格)效应。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删