基于Runge-Kutta算法的硬化土模型二次开发实践

摘    要：

硬化土模型在描述软土和较硬土的变形特性上有较好的表现，文章结合有限元软件ABAQUS中的UMAT二次开发平台，编写了硬化土本构模型子程序，提高了硬化土模型的泛用性，并提出了通过NewtonRapson迭代、Runge-Kutta迭代等数值方法求解任意应变增量对应的应力增量，最后通过室内三轴压缩试验数据验证了程序的正确性和合理性。

关键词：硬化土模型;应力更新算法;ABAQUS;二次开发;

随着现代岩土工程的发展，工程建设中遇到的问题逐渐从简单的稳定性分析转变为较精细的变形分析，能否精准地进行变形分析通常取决于计算使用的本构模型[1]。由于岩土体复杂，尽管目前已提出了上百种本构模型，但大多数模型仅能反映特定土体在特定情况下的力学行为，因此存在一定的局限性。岩土工程常用的Mohr-Coulomb模型和Drucker-Prager模型为理想弹塑性本构模型，MCC模型为硬化弹塑性模型，难以同时反映土体的剪切硬化和压缩硬化，采用Mohr-Coulomb强度理论作为屈服准则，从Vermeer双硬化模型发展而来的硬化土（HS）本构模型[2]作为一种双屈服面硬化弹塑性本构模型，在描述软土和较硬土的变形特性上有较好的表现[3]。

目前，除了PLAXIS、ZSoil等少数有限元软件已嵌入HS模型，其他软件使用该本构仍需自行开发编写相关程序。ABAQUS软件在求解岩土等非线性问题上有突出的优势，有能为用户提供编写自定义本构模型的二次开发平台。徐远杰等[4]将Duncan-Chang本构模型成功编成了UMAT子程序，岑威钧和朱岳明[5]推导了平面应变条件下UMAT子程序所需的弹塑性刚度矩阵，为后续学者开发UMAT子程序提供了支撑，使许多本构模型被广泛应用于岩土工程数值模拟中。因此，为有效地扩展HS模型的应用范围，可选用ABAQUS作为HS模型的开发平台。

为实现HS模型在ABAQUS上的应用，文章利用ABAQUS用户自定义材料子程序（UMAT）编写HS本构模型，优化其应力更新算法，并将模型的计算结果与室内三轴压缩试验数据进行对比，验证该本构模型的合理性及可靠性，还分析了采用其他本构时数值模拟的结果。

1 硬化土模型

硬化土模型中土体的刚度与应力相关[4]。土体处于弹性阶段时，采用双刚度分别模拟加载与卸载时的力学特性，如图1所示。土体处于塑性阶段时，采用各向同性硬化法则与非关联的流动法则反映土体的剪胀性，同时引入帽盖屈服面反映土体的压缩硬化，形成了双硬化本构模型[5]。

图1 硬化土模型弹性阶段应力-应变关系

1.1 剪切屈服面

HS模型的剪切屈服面可用如下公式表示：

式中：Fs为剪切屈服函数；qa为极限偏应力；E50为对应50%强度时的割线模量；q为剪应力；Eur为卸载再加载模量；γ p为塑性剪切应变。

式中：E50ref为对应参考围压σref时的E50模量；σ3为第三主应力；c为黏聚力；φ为摩擦角；m为与土体性质有关的幂指数。

式中：Eurref为对应参考围压σref时的Eur模量。

式中：σ1为第一主应力；f为处于破坏时的状态；Rf为破坏比。

1.2 塑性势函数

HS模型剪切屈服面采用的是不相适应的流动规则，其剪切塑性势函数如下：

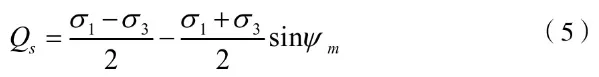
式中：Qs为剪切塑性势函数；ψm为机动剪胀角，由于不允许负剪胀角的存在，当ψm<0时，取0。

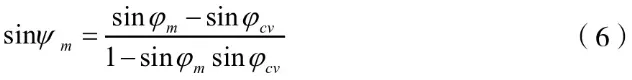
式中：φm为机动摩擦角；φcv为临界摩擦角。

式中：φ为土体固有剪胀角。

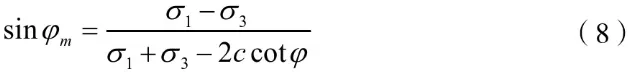
1.3 压缩屈服面

HS模型中为体现土体压缩硬化特性加入了帽盖屈服面，其屈服函数如下：

式中：F为压缩屈服函数；δ为土体计算参数；σ2为第二主应力；M为摩擦常数；Pc为前期固结应力。

压缩屈服面采用的是相适应的流动规则，其硬化定律如下：

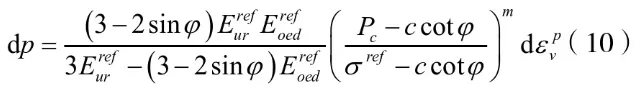
式中：dp为硬化参数增量；Eoedref为切线模量；dεvp为塑性应变增量。

2 应力更新计算方法优化

ABAQUS中编写自定义本构模型需要推导出在笛卡尔三维（或二维）坐标系下单元积分点的雅可比矩阵DDSDDE，即求解出该积分点各应力增量对应变增量的变化率∂σ/∂ε，并据此对该增量步的总应力和状态变量进行更新、输出，通过接口返回ABAQUS主程序[6]。

2.1 变形阶段划分与试探应力

对任意传入的应变增量，先假定其全部为弹性应变，由广义胡克定律可得材料的弹性刚度矩阵：

式中：[De]为弹性刚度矩阵；λ为拉梅常数；G为剪切模量。

式中：E为弹性模量；μ为泊松比。

式中：{∆σn+1}为第n+1步的应力增量张量；{∆σen+1}为第n+1步的弹性应力增量张量。

式中：为试探应力；为第n步的应力张量；{∆σn+1}为第n+1步的应力张量。

将代入式（1）和式（9），若，则增量步全程处于弹性阶段；若，则增量步从弹性阶段过渡至弹塑性阶段；若，则增量步全程处于弹塑性阶段。

2.2 应力更新计算

在弹塑性阶段，材料在从到的过程中必然会经过屈服应力状态，在从到此段内只发生弹性变形，仅须用弹性刚度矩阵[De]更新应力即可。在到这段则发生弹塑性变形，须求得弹塑性刚度矩阵[Dep]进行求解。因此，为求解整个增量步的应力变化，须确定在屈服面上的位置，可设：

式中：r为比例因子；为第n+1步的屈服应力张量。

则：

由在屈服面上可得：

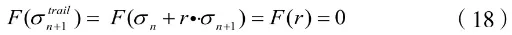
式中：为关于判断应力的函数；F (σn+r·⋅σn+1)为关于应力及参数r的函数；F(r)为关于r的函数。

F(r)形式较复杂，很难求得准确的解析解，因此可用Newton-Rapson迭代法求出数值解，鉴于Newton-Rapson迭代法对初值的要求较高，可先采用二分法大致确定初值范围后再进行迭代计算，迭代方程如下：

式中：rk+1为第k+1个参数r;rk为第k个参数r;F(rk)为关于rk的函数；F'(rk)为关于rk的函数的导函数。

得到r后，可将分成弹性增量{∆σen+1}和弹塑性增量{∆σepn+1}两部分，通过弹性刚度矩阵反算得到真实弹性应变增量{∆εe}：

式中：{∆ε n+1}为第n+1步的应变增量。

由上式可得弹塑性应变增量{∆ε ep}。

弹塑性阶段的应力更新求解式如下：

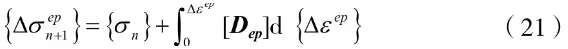
式中：∆εep为塑性应变增量；为对塑性应变求积分。

2.3 应力更新迭代算法

弹塑性阶段时，材料的弹塑性刚度矩阵是关于应力的函数：

式中：[Dep]为材料的弹塑性刚度矩阵；σ为应力。

在积分时，[Dep]会随着应力的变化而变化，积分的求解将十分困难。在ABAQUS中一般使用显式欧拉方程进行应力更新，针对这种情况，要将步长缩小，以保证程序计算的收敛性，极大地降低了计算效率。使用Runge-Kutta迭代法对式（21）进行数值求解，能减少程序迭代计算的次数。因此文章使用Runge-Kutta法求解该常微分方程，迭代方程如下：

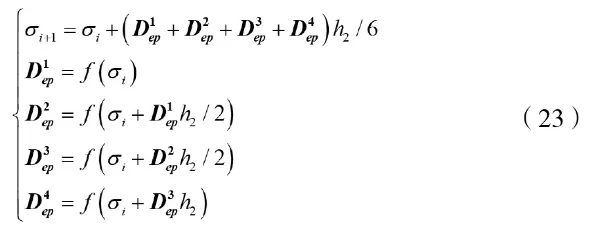
式中：σi+1为第i+1步时的应力；σi为第i步时的应力；Diep为不同σi时对应的弹塑性刚度矩阵；h2为迭代步长，通过公式计算可得或按需选取。

模型的弹塑性刚度矩阵为一般形式：

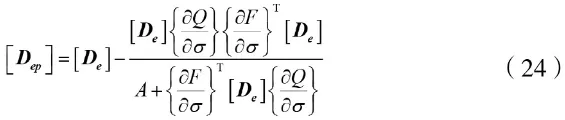
式中：A为塑性硬化模量，是硬化参数的函数；F、Q分别为屈服函数和塑性势函数，采用相适应流动规则时两者相等；∂Q为对塑性势函数求偏导；∂F为对屈服函数求偏导；∂σ为对应力求偏导；T为线性代数矩阵转置符号。

3 HS模型在程序中的实现

在计算中，ABAQUS主程序会调用用户编写的UMAT子程序，将主程序各单元积分点上的应力、应变传递给子程序[7]。子程序通过本构关系计算得到雅可比矩阵及迭代更新后的应力、应变和用户设置的状态变量，并将相应数据回传给ABAQUS主程序。计算过程中，每一增量步的各迭代步都需调用UMAT子程序，直至全部增量步计算完成[8]。

一般来说，ABAQUS中UMAT子程序的编写需要采用Fixed Format，但通过修改ABAQUS配置文件“win86＿64.env”可将UMAT编写格式修改为Free Format，简化UMAT子程序的编写流程，修改后原UMAT接口的固定格式也需相应修改[9],UMAT子程序接口固定格式示意图如图2所示。

图2 UMAT子程序接口固定格式示意图

采用模块化程序设计理念编写UMAT子程序，即将需要重复使用的代码功能整合成独立运行的小模块，当有需要时再调用，显著提高了程序代码的可读性及修改效率[10]。流程图如图3所示。

4 模型验证

4.1 算例简介

为验证编写的UMAT子程序的准确性和可靠性，在ABAQUS上使用UMAT子程序对三轴压缩试验模型进行数值模拟，并与室内三轴试验结果进行对比。数值模型为直径39.1 mm、高80 mm的标准三轴试样。模型边界条件如下：底面设置法向位移约束；侧面根据不同工况施加不同的径向压力（125 kPa、225 kPa和300 kPa）；顶面施加分级荷载，先施加与围压相等的固结压力模拟试样的固结过程，再逐级加载至试样破坏[11]。模拟材料为花岗岩残积土，土体相应的参数由三轴试验得到，具体数值如表1所示。

图3 HS模型UMAT子程序流程图

4.2 结果对比

将数值模型计算结果与室内三轴试验数据进行对比，具体结果如图4所示。从图4可以看出，花岗岩残积土在应力软化前的应变-应力关系类似于双曲线，与HS模型弹性阶段变化趋势相吻合[12]。在不同围压尤其是125 kPa和225 kPa下，数值模型计算结果与试验数据均一致，充分表明了文章开发的HS模型子程序的可靠性和准确性[13]。

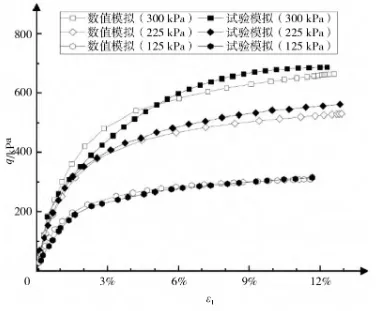
图4 不同围压HS本构数值模拟结果与试验数据对比

表1 土体计算参数

为了对比HS模型与现有本构模型，文章将开发的HS模型与ABAQUS中的Mohr-Coulomb模型进行比较，将数值结果与试验实测数据进行对比，结果如图5和图6所示。从图5、图6可以看出，尽管Mohr-Coulomb模型能在一定程度上表现土体的应力-应变行为，但与HS模型相比仍有较大差距，HS模型既能体现土体变形前段的双曲线应力-应变关系，又能很好地反映土体剪切屈服平台，这充分表明了在ABAQUS上进行HS模型开发的必要性[14]。

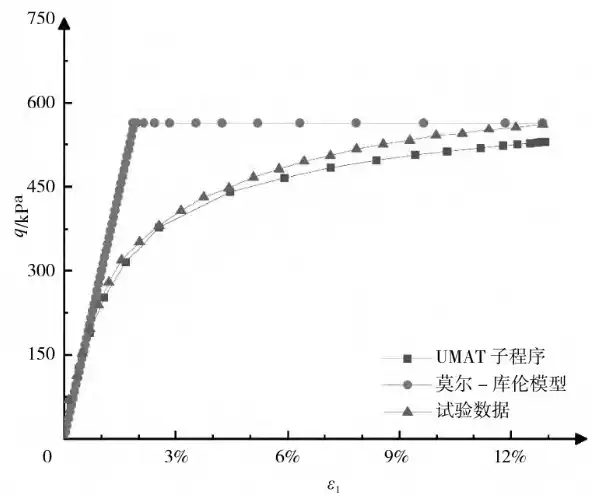
图5 不同本构模型三轴试验数值模拟结果对比（σ2=200 k Pa)

图6 不同本构模型三轴试验数值模拟结果对比（σ2=300 k Pa)  

5 结论

文章利用ABAQUS的二次开发平台完成了硬化土模型的数值实现，并成功将其应用于三轴试验相关的数值模拟计算，得到了以下成果：

1）推导出HS模型在不同应力状态下的应力更新计算公式，提出了对任意给定应变增量均可通过Runge-Kutta迭代等数值方法求解相应应力增量的算法。

2）通过三轴压缩模拟实验验证了HS模型UAMT子程序开发的可靠性和必要性，并通过与其他本构模型对比，证明了HS模型能很好地模拟土体的应力应变关系。

3）基于Runge-Kutta算法及Newton-Rapson迭代法对UMAT进行优化的算法设计流程及思路可以为其他本构模型的开发提供借鉴，进一步促进岩土工程数值分析技术的发展。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删