MATLAB数学运算：向量求导、拉丁超立方采样与QR分解

最近一直在回炉重造。中间有的时候也会有一些感想，有的已经忘记了，趁还没有忘记一些东西，先写下来为妙。首先是向量对于向量求导。百度上：　

3. 行向量Y'对列向量X求导： 　　注意1×M向量对N×1向量求导后是N×M矩阵。 　　将Y的每一列对X求偏导，将各列构成一个矩阵。 　　重要结论： 　　dX'/dX = I 　　d(AX)'/dX = A'

这个其实很好理解，下面是一各例子，第一行只是把两个函数放到了一个行向量里面而已。

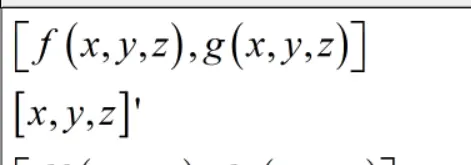
然后从全微分的角度理解。

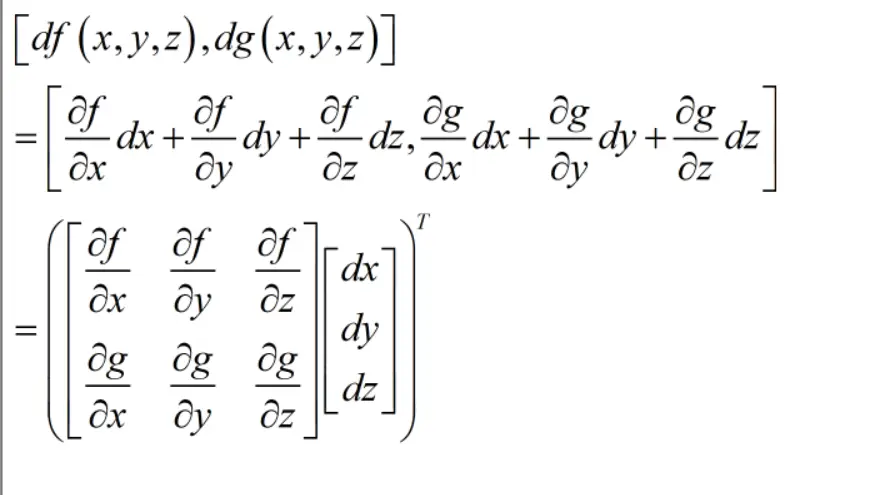
　最后比较难受的就是这个最好结果需要转置，不过转置之后，就是3x2的了。不过dx,dy,dz就是行向量了，挺难受的，所以我看见更多的还是对于列向量求导。

　4. 列向量Y对行向量X’求导： 　　转化为行向量Y’对列向量X的导数，然后转置。 　　注意M×1向量对1×N向量求导结果为M×N矩阵。 　　dY/dX' = (dY'/dX)'

4其实和3差不多。

如果是列向量对于列向量求导就会舒服很多。

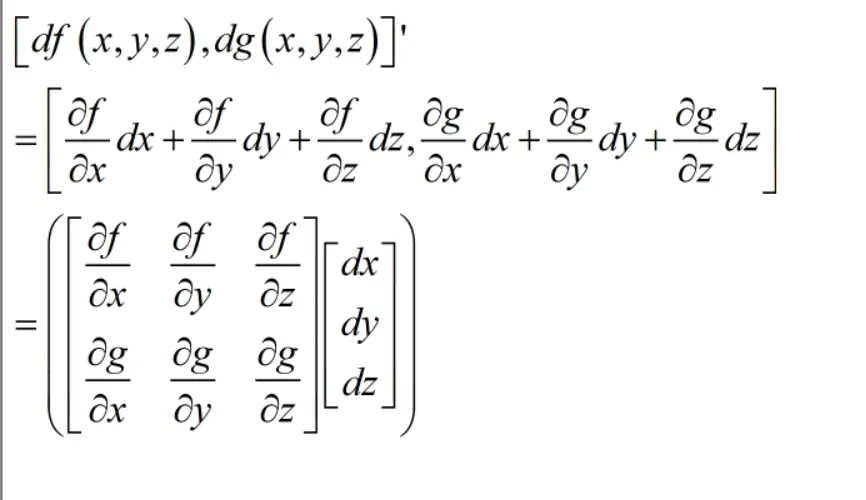
这下应该不会忘记为什么雅可比矩阵的每一行都是函数对每一个变量求求偏导了吧。

当然我觉得只有行对行求和列对列求是正统的，其它的感觉都是定义的。

这里我还想到了伴随行列式为什么要转置呢？就是代数余子式的位置和原来的位置是转置关系，因为在乘的时候（A,B,C,D分别代表对应位置的代数余子式），左边的第一行乘以伴随真的第一列，按照行列式展开，显然对应元素应该乘以对应的代数余子式加起来等于行列式然后除以行列式等于1，所以需要转置。

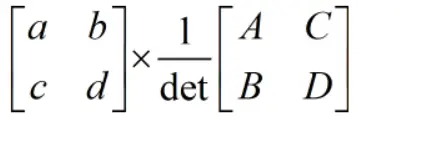
这里只是举了一个例子，高维的也一样。那么第一行的元素乘以第二行代数余子式为什么等于0呢？可以这样想，首先C和D里面肯定是有a和b这一行的。所以就是说相当于原来的矩阵有相同的两行，所以行列式为0。

拉丁超立方采样

这个最近学了一下感觉挺有意思的，所以就来学一下。它是实验设计的一种，实验设计还有用正交表的，均匀表的。

拉丁超立方抽样（英语：Latin hypercube sampling，缩写LHS）是一种从多元参数分布中近似随机抽样的方法，属于分层抽样技术，常用于计算机实验或蒙特卡洛积分等。

麦凯（McKay）等人于1979年提出了拉丁超立方抽样。不过此前Eglājs于1977年独立提出过相同的抽样技术。1981年，伊曼（Ronald L. Iman）等进一步发展了该方法。

在统计抽样中，拉丁方阵是指每行、每列仅包含一个样本的方阵。拉丁超立方则是拉丁方阵在多维中的推广，每个与轴垂直的超平面最多含有一个样本。

假设有N个变量（维度），可以将每个变量分为M个概率相同的区间。此时，可以选取M个满足拉丁超立方条件的样本点。需要注意的是，拉丁超立方抽样要求每个变量的分区数量M相同。不过，该方法并不要求当变量增加时样本数M同样增加。

假设我们要在n维向量空间里抽取m个样本。拉丁超立方体抽样的步骤是：

（1） 将每一维分成互不重迭的m个区间，使得每个区间有相同的概率 （通常考虑一个均匀分布，这样区间的长度相同）。

（2） 在每一维里的每一个区间中随机的抽取一个点；

（3） 再从每一维里随机抽出（2）中选取的点，将它们组成向量。这一步主要是为了打乱。

扩展资料：

拉丁超立方抽样和蒙特卡罗模拟的区别：

1、蒙特卡罗抽样技术完全是随机的，即在输入分布的范围内，样本可以落在任何位置。样本更有可能从高发生概率的分布区域中抽取。在累积分布中，每个蒙特卡罗样本使用一个0 和 1之间的新的随机数。在足够的迭代之后，蒙特卡罗抽样通过抽样“重建”输入分布。但是，当执行的迭代次数少的时候，会产生聚集的问题。

2、拉丁超立方体抽样是抽样技术的最新进展，和蒙特卡罗方法相比，它被设计成通过较少迭代次数的抽样，准确地重建输入分布。拉丁超立方体抽样的关键是对输入概率分布进行分层。分层在累积概率尺度（0，1.0）上把累积曲线分成相等的区间。然后，从输入分布的每个区间或“分层”中随机抽取样本。抽样被强制代表每个区间的值，于是，被强制重建输入概率分布。

假设我们要在n维向量空间里抽取m个样本。拉丁超立方体抽样的步骤是：

（1）将每一维分成互不重迭的m个区间，使得每个区间有相同的概率（通常考虑一个均匀分布，这样区间的长度相同）。

（2）在每一维里的每一个区间中随机的抽取一个点；

（3）再从每一维里随机抽出（2）中选取的点，将它们组成向量。

在抽样时，每个区间都抽取一个样本。使用拉丁超立方体方法，样本更加准确地反映输入概率分布中值的分布。在拉丁超立方体抽样中使用的技术是“抽样不替换”，累积分布的分层数目等于执行的迭代次数。

拉丁超立方采样的均匀性更好。还参考了https://wenku.baidu.com/view/1e6c65d1fab069dc50220128.html

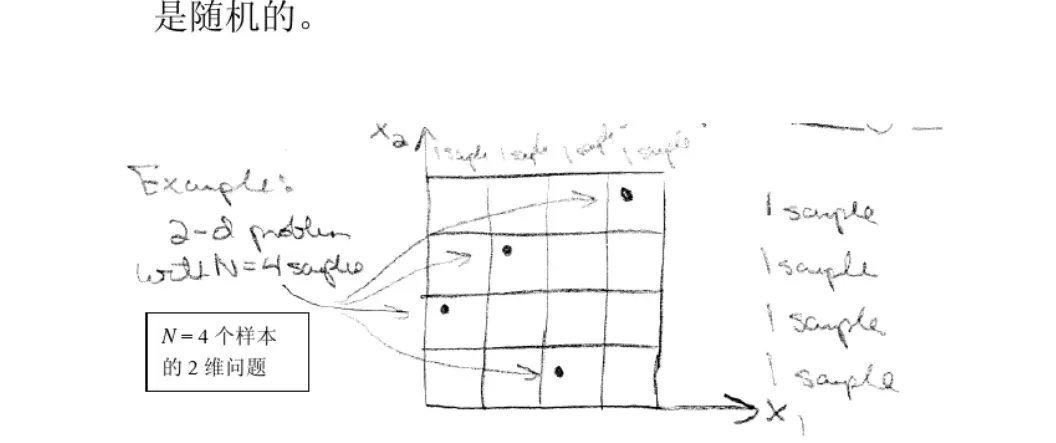
这种方法直观的看就是图上每一列都只有一个栅格内有点，而每一行也是一样。对于16种可能它只取了4个点。

这个matlab函数里面也有lhsnorm这个是正态分布的，lhsdesign还有lhspoint都可以做均匀分布的。拉丁超立方是要让均值等于原来的均值而方差尽可能小。

这个如果以后有进一步的理解会继续更新。

matlab qr分解的坑

做实验的时候用到了qr分解，python的numpy的qr分解没有问题，输入一个非方阵的时候，q是非方阵，r是方阵，matlab q是方阵，r是非方阵......，它肯定不是用施密特正交化求的，所以我自己还得编一个施密特正交化程序。这里需要注意首先要找到列向量的极大无关组，然后再对极大无关组施密特正交化，其它的向量可以用极大无关组里面的表示。

怎么找极大无关组呢，可以试试rref。

numpy索引的小问题

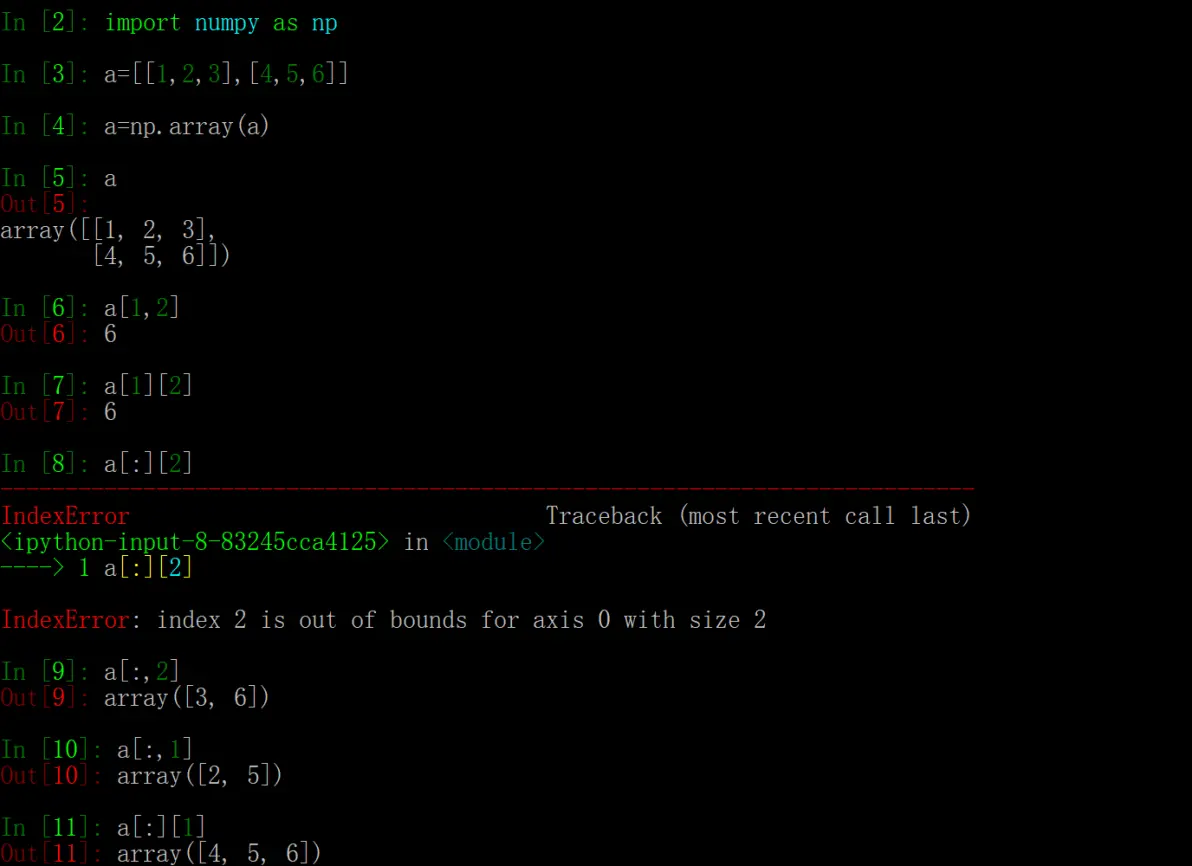
在索引一个元素的时候，用逗号和多个中括号索引没有区别，但是如果是用了冒号或者...，那么就会有区别，一般来说获得所有行的第二列是用[:,2]，而[:][2]是所有行的第二行，这个是优先级的问题。