在进行lyapunov指数的求取时,需要知道离散动力学系统对应Jacobi矩阵的特征值,qr法与Jacobi法都可以求解矩阵特征值,其中qr法求解的是矩阵所有特征值,而Jacobi法求解的是矩阵的最大特征值。本文以二维Henon映射为例,分别展示两种方法在求解时的区别与联系。
1.准备工作
1.1 henon映射
动力学系统
Henon映射为二维映射,其动力学方程通常有以下两种写法:
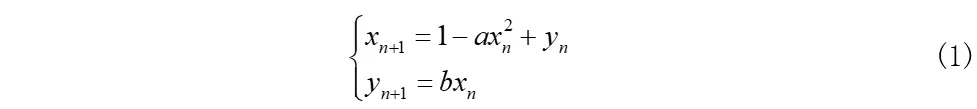
和
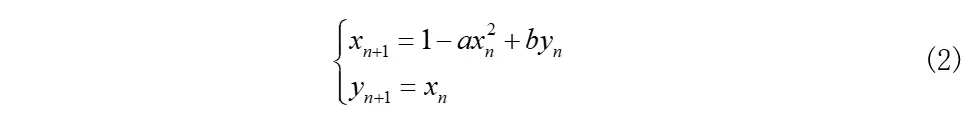
式中a、b为参数,0<b≤1,我们通常运用式(1)表达形式。
代码实现
clc;clear all;close all
%初值设置
x0=0.2;y0=0.3;
%参数设置
b=0.3;n=800;t=600;
hold on
for a = 0:0.01:1.4 %参数a
x(1)=1+y0-a*x0^2;
y(1)=b*x0;
for i =2:n
x(i)=1+y(i-1)-a*x(i-1)^2;
y(i)=b*x(i-1);
end
xn=x(t+1:n);%取80次迭代之后的数据
pause(0.1);
plot(a,xn,'r.','Markersize',2);
xlabel('a');ylabel('x');
set(gca,'XLim',[0 1.4]);
set(gca,'XTick',[0:0.2:1.4]);
set(gca,'YLim',[-1.5 1.5]);
set(gca,'YTick',[-1.5:0.5:1.5]);
end混沌图像:
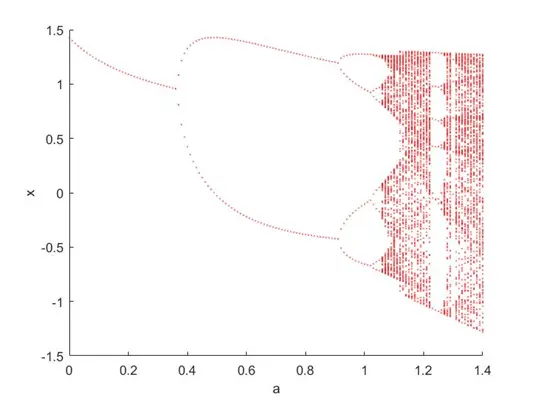
图1 .henon映射
1.2 jacobi矩阵
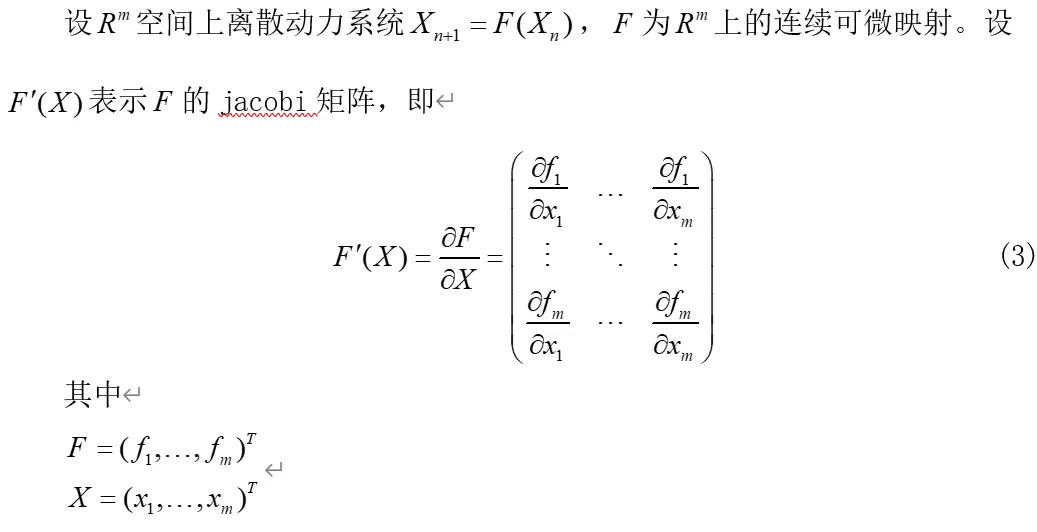
求Jacobi矩阵,实际上就是对动力学系统方程关于求偏导。
1.3 lyapunov指数
在式(3)jacobi矩阵的基础上有
首先令:
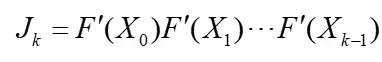
Jk的m个复特征值表示为:
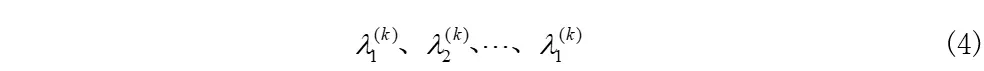
离散动力学系统的第个lypunov指数可表示为:
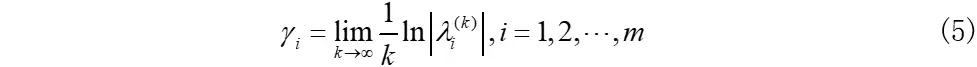
2. Jacobi法
Jacobi法求特征值,是求的最大特征值。故在(4)式的基础上,我们应将特征值进行排序,然后取出最大的特征值即可,但是:
①在求lypunov指数是特征值取模;
②对于复特征值而言不取模的话并无意义;
③对于单纯数大,但数值并不大的特征值而言,其对应求得的lypunov指数并没有十分特殊的意义;
④特征值模最大,可以对应求得系统的最大lypunov指数,对于henon映射这种2维系统而言,对最大lypunov指数进行观察就可以了解系统混沌与否。
故我们对(4)式中的特征值,进行取模排序,依次从小到大排序为:
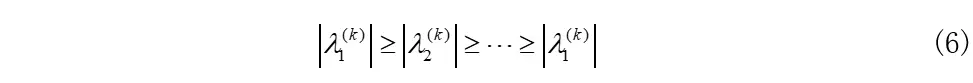
那么利用jacobi法求系统特征值后所对应的lypunov指数可表示为:
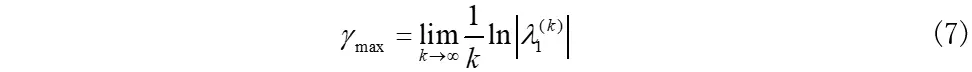
代码实现
clc, clear
a=0:0.01:1.6; n=500; S=[];
for j=1:length(a)
x=0.2; y=0.3; %x,y的初值
for i=1:n
x2=1-a(j)*x^2+y; y=0.3*x; x=x2; %首先进行序列迭代
end
if x(end)>-100 & x(end)<100 %若不发散,再计算指数
x=0.2; y=0.3;
JJ=eye(2);%2阶单位矩阵
for i=1:n
x2=1-a(j)*x^2+y; y=0.3*x; x=x2;
J=[-2*a(j)*x, 1; 0.3, 0];%jacobi矩阵
JJ=JJ*J;
end
L=eigs(JJ,1); %求模最大的特征值,并返回1个最大特征值
S=[S,[a(j);log(abs(L))/n]]; %把a值及指数值保存
end
end
plot(S(1,:),S(2,:),'.-') %画出a对应的最大Lyapunov指数
hold on, plot([a(1),a(end)],[0,0],'k')
xlabel('\it a'), ylabel('最大Lyapunov指数')lypunov指数谱:
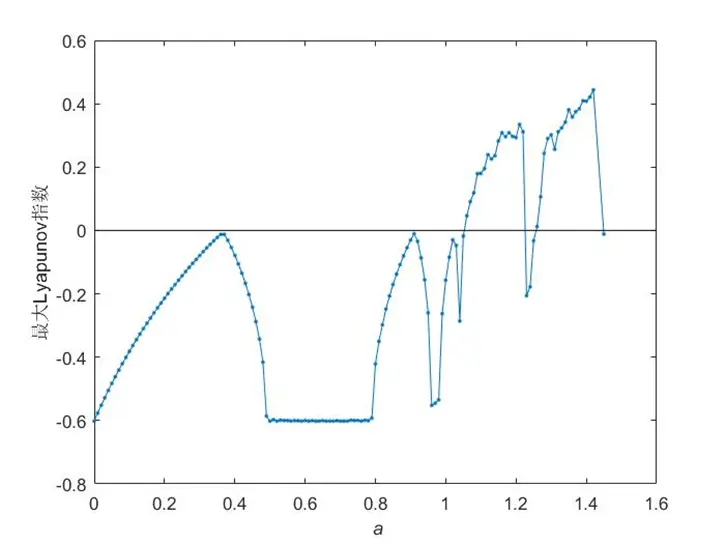
图2 .jacobi法求得的henon映射lyapunov指数谱
jacobi法求得的lyapunov指数谱与混沌的对应:
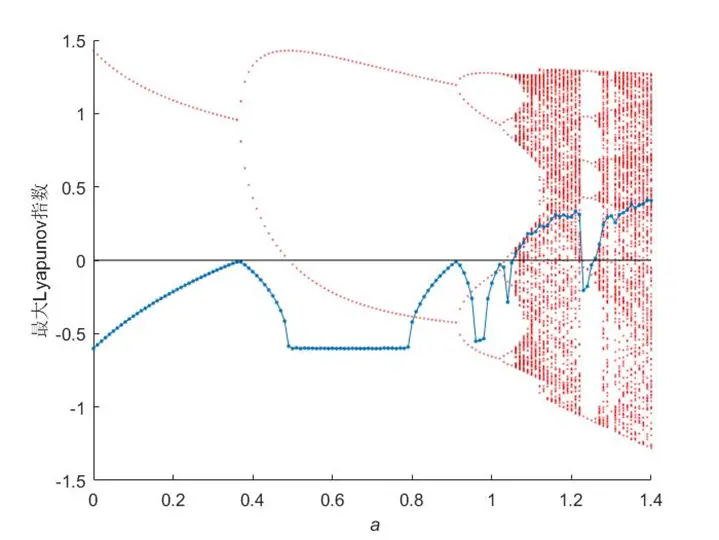
图3 .jacobi法求得的henon映射与最大lyapunov指数之间的对应
3. qr法
qr法求的是系统所有的特征值,即把式(4)中所有特征值,进行取模后全部转化为lyapunov。由于henon映射为2维系统,故其对应的特征值最多就2个:
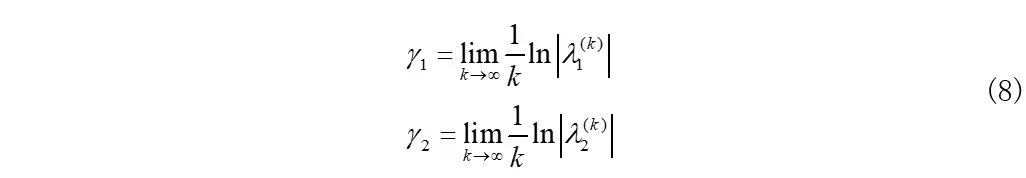
代码实现
clc;close all;clear all
N = 1000;
a = (0:0.001:1.4)';
b = 0.3;
na = length(a);
LE1 = zeros(na,1);
LE2 = zeros(na,1);
x = 0.2; y = 0.3;
for i=1:na
LCEvector = zeros(2,1);
Q = eye(2);
for j=1:N
xprev = x;
yprev = y;
x = 1-a(i)*xprev*xprev+yprev;
y = b*xprev;
Ji = [-2*a(i)*x,1;b 0];
B = Ji*Q;
[Q,R] = qr(B); %R得B矩阵的上三角矩阵
LCEvector = LCEvector+log(diag(abs(R)));
end
LE = LCEvector/N;
LE1(i) = LE(1);
LE2(i) = LE(2);
end
figure(1)
plot(a,LE1,'g','linewidth',1) ;
hold on
plot(a,LE2,'b','linewidth',1);
set(gca,'XLim',[0 1.4]);
set(gca,'YLim',[-2 1]);
legend('\lambda1','\lambda2');
hold on
plot([0 1.4],[0 0],'k--','linewidth',1)
hold off
xlabel('a');ylabel('LE');
set(gca,'fontsize',10)lyapunov指数谱:
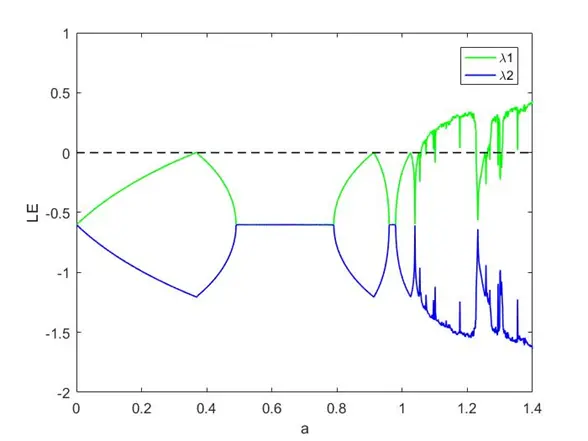
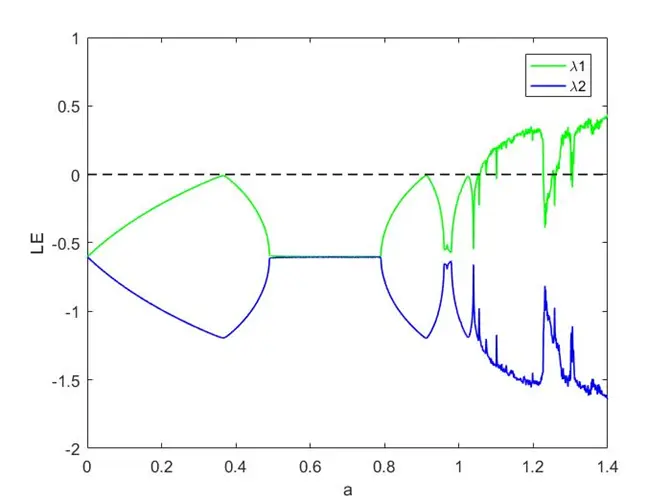
图4 .qr法求得的henon映射lyapunov指数谱
4. qr法与Jacobi法之间代码的联系
在jacobi法代码基础上,我们稍作调整也可以得qr法对应的lyapunov指数谱:
①去掉eigs()这个求最大特征值函数
②引入qr函数
③jacobi法每次对应1个特征值,qr法此处对应两个,因此为了累加计算的方便将lyapunov指数迭代放到循环里面。
代码实现
clc, clear
a=0:0.001:1.4; n=500;
for j=1:length(a)
LE = zeros(2,1);
x=0.2; y=0.3; %x,y的初值
for i=1:n
x2=1-a(j)*x^2+y; y=0.3*x; x=x2; %首先进行序列迭代
end
if x(end)>-100 & x(end)<100 %若不发散,再计算指数
x=0.2; y=0.3;
JJ=eye(2);%2阶单位矩阵
for i=1:n
x2=1-a(j)*x^2+y; y=0.3*x; x=x2;
J=[-2*a(j)*x, 1; 0.3, 0];%jacobi矩阵
JJ=J*JJ;
[JJ,L]=qr(JJ);
LE = LE+log(diag(abs(L)));
end
end
LE = LE/n;
LE1(j) = LE(1);
LE2(j) = LE(2);
end
figure(1)
plot(a,LE1,'g','linewidth',1) ;
hold on
plot(a,LE2,'b','linewidth',1);
set(gca,'XLim',[0 1.4]);
set(gca,'YLim',[-2 1]);
legend('\lambda1','\lambda2');
hold on
plot([0 1.4],[0 0],'k--','linewidth',1)
hold off
xlabel('a');ylabel('LE');
set(gca,'fontsize',10)lyapunov指数谱: