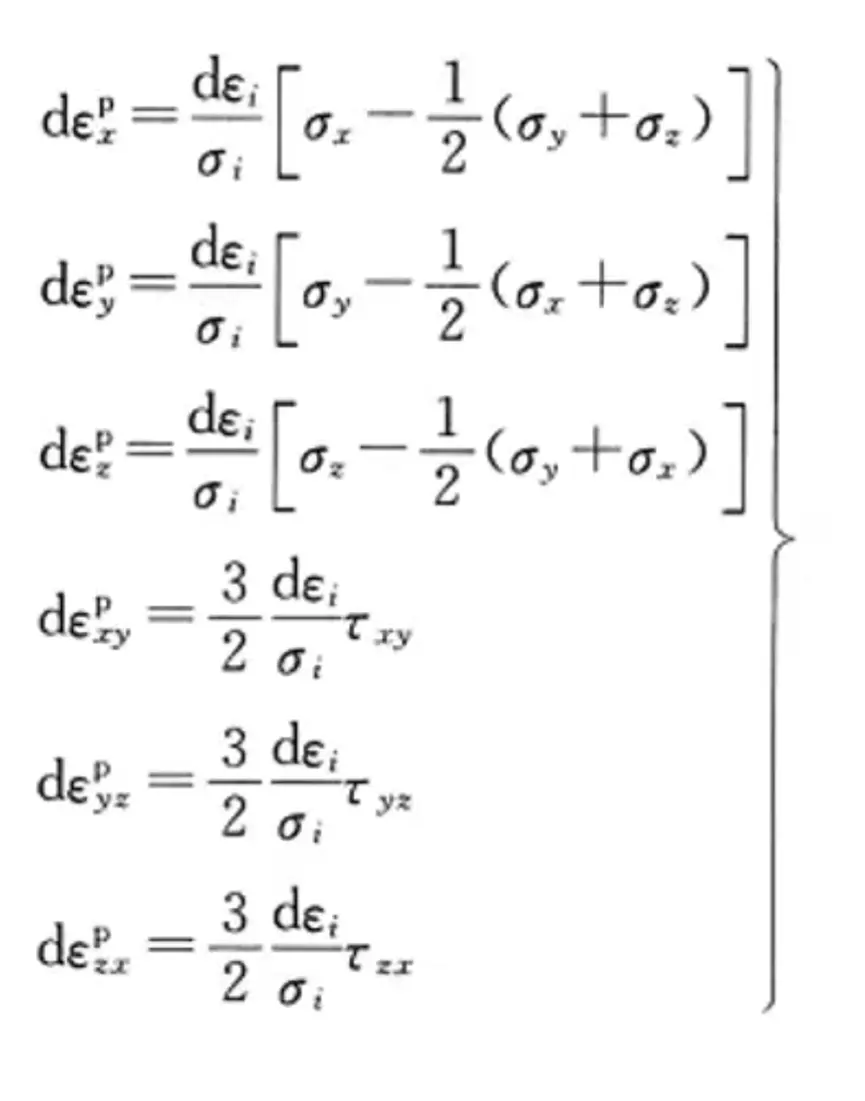跟兵哥学ABAQUS子程序：弹塑性UMAT理论

判断塑性变形是否发生的条件是屈服条件。而屈服之后，也就是塑性变形的阶段，本构关系与弹性时的本构关系是不同的。这时候的本构叫塑性本构，或称流动法则。

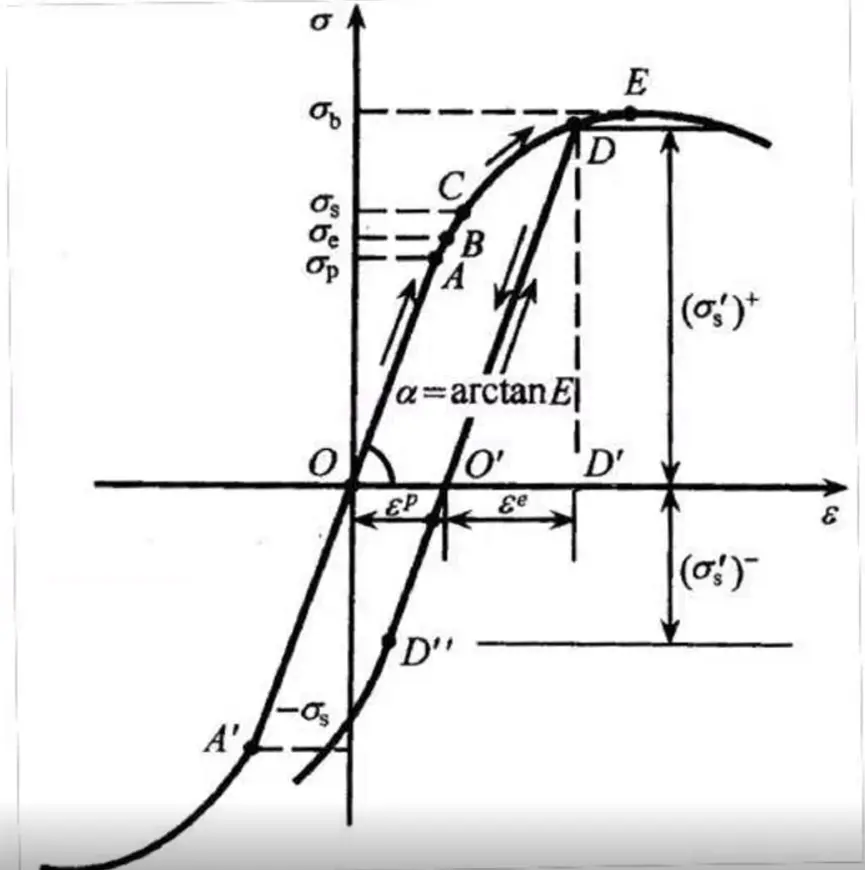
材料单向拉伸实验的应力应变关系如图所示。从O点开始，逐步增大外力（加载），应力状态先沿着OA线性爬升，到B点的时候，就发生屈服了。在这之前，是弹性阶段。在B点之后，是塑性阶段。继续沿着曲线走，到D点的时候，逐步卸载外力。曲线就沿着DO’向下线性地返回。可以看到O’点是完全不加外力的时候，但是这时候还残留了变形，这就是因为发生了不可恢复的塑性变形，叫残余应变。这时候，即使再重新从0开始加载外力，就会沿着O’开始往上走，直到D点发生屈服。可见，从表面上看，屈服应力变大了，这被称之为屈服强化现象，也称之为屈服硬化。屈服强化在主应力空间上的几何表示就是屈服柱面移动了（半径扩大（称为等向强化）或者圆心位置改变（称为随动强化/Bauschinger效应））。

总结一下：

1. 什么时候发生塑性变形，即对应B点怎么确定？--屈服准则。
2. 发生塑性变形之后是怎么样的，即BD曲线是什么样的？--流动法则，或称塑性本构。
3. 已经塑性变形过的材料再次加外力时屈服应力增大了多少，即D点是如何确定的？--后继屈服准则，或称强化准则。

---

塑性本构这块还没看懂，先贴上截图记录

塑性本构和弹性本构最大的区别在于：塑性本构是增量关系。

这是因为塑性是历史路径相关的，必须一步步走。（不知是不是对：弹性力是物理里面的保守力，类似重力；塑性力是非保守力，类似摩擦力。）

所以通常用增量本构来表示本构关系，一句话：

塑性应变增量与瞬时应力偏量成正比。

这个比例系数定义为dlambda。这个dlambda是个变量，不是个常数。不仅如此，dlambda还跟应变本身有关。这就注定了是非线性的。

经过前人推导，得到dlambda就是下面这个式子。可以看出，它和应力应变是有关系的。

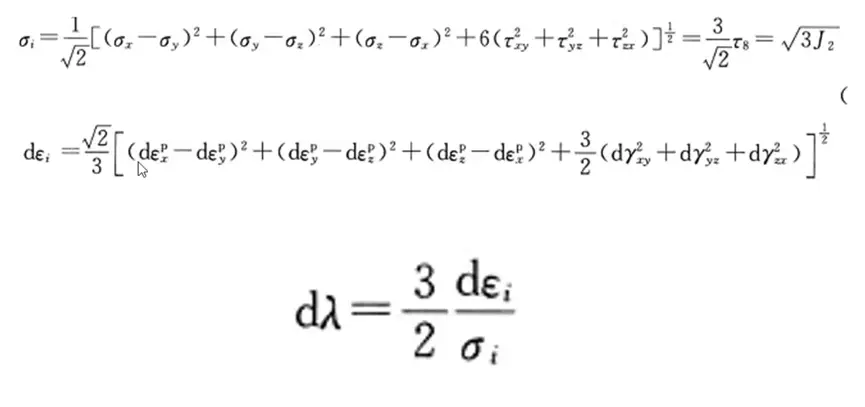
最后把dlambda带回到那个正比例关系里面，得到了本构方程：