各向同性硬化von Mises率无关弹塑性本构理论以及umat源代码

1 本构理论

1.1 率形式

对于各向同性线弹性材料，其本构方程为：

式中假设了应变张量可以分解为弹性应变和塑性应变两部分：

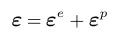
因此塑性本构的关键在于计算塑性应变的演化。对于率无关弹塑性的本构理论，需要确定以下三个部分：

(1)：屈服条件

(2)：流动法则

(3)：硬化法则

在此采用的是 von Mises 屈服条件：

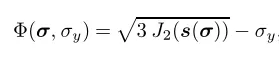
式中后继屈服应力是等效塑性应变的函数：

流动法则为：

式中流动方向的表达式为：

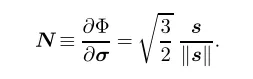
硬化法则为：

1.2 Return-mapping算法

上述的本构方程均为率形式。在增量步中，给定增量应变：

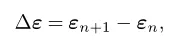
首先假设该增量应变全为弹性应变，计算试验状态下的一些物理量：

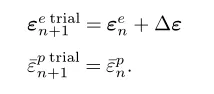
试验状态下的应力

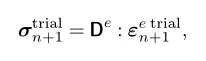
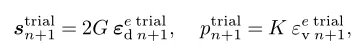
试验状态下的屈服函数值：

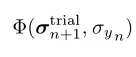
利用该试验屈服函数值来判断在该增量步下是否发生了塑性屈服。如果：

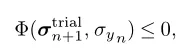
则说明试验状态即为真实状态，即可进行更新：

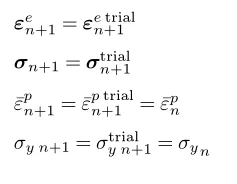
反之则需要进行塑性更正，即需要计算塑性乘子的增量，利用以下非线性方程组进行计算：

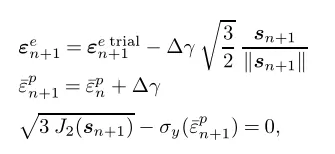
可以将该非线性方程组简化至一个非线性方程，过程如下，将该方程组中的第一式分解为球量和偏量两部分：

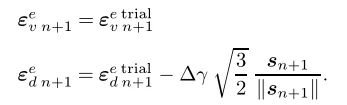
因此可以计算应力为：

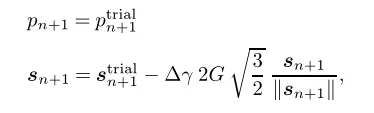
将上式中的第二式整理得到：

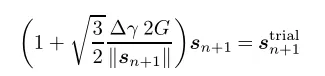
可以得到两个张量的方向相同：

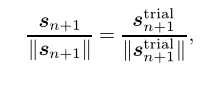
因此偏应力可以用试验状态的信息表示出来：

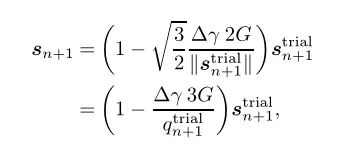
代入到最后一个一致性方程中可得：

即可利用牛顿迭代法对上述非线性方程进行求解，得到塑性乘子增量。求解得到塑性乘子增量之后，即可更新：

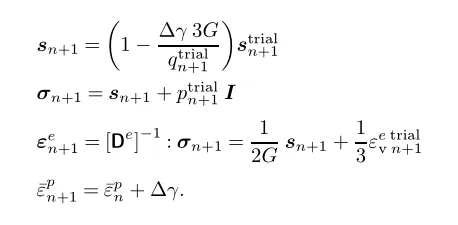
也可以更新塑性应变：

1.3 一致性切线刚度矩阵

umat除了要求更新应力以及状态变量之外，还需要更新算法的一致性切线刚度模量。当没有发生塑性屈服时，一致性切线刚度矩阵即为弹性矩阵。当发生塑性屈服时，根据应力更新的公式：

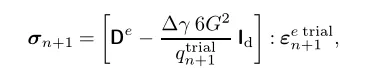
可以计算：

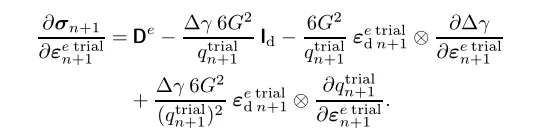
式中：

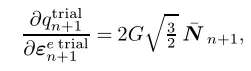
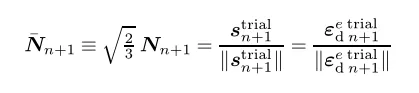
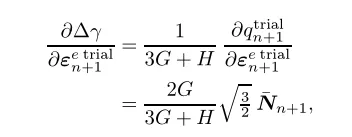
式中：

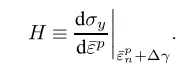
为硬化曲线的梯度，各向同性硬化曲线使用数据点拟合为分段线性函数：

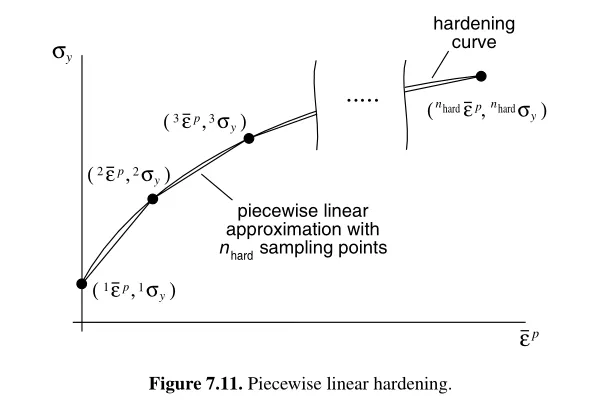
因此最终可得到一致性切线刚度矩阵的表达式为：

2 算法描述

整个 return-mapping 算法框图如下：

牛顿迭代法算法框图如下：

3 UMAT代码

umat使用F90编写，其主程序如下：

include "plastic_iso_pack.f90"


subroutine UMAT(stress,statev,ddsdde,sse,spd,scd,                       &
                rpl,ddsddt,drplde,drpldt,                               &
                stran,dstran,time,dtime,temp,dtemp,predef,dpred,cmname, &
                ndi,nshr,ntens,nstatv,props,nprops,coords,drot,pnewdt,  &
                celent,dfgrd0,dfgrd1,noel,npt,layer,kspt,kstep,kinc)


    use plastic_iso_pack


    include 'aba_param.inc'


    character*80 cmname
    dimension    stress(ntens),statev(nstatv),ddsdde(ntens,ntens),   &
                ddsddt(ntens),drplde(ntens),                        &
                stran(ntens),dstran(ntens),time(2),                 &
                predef(1),dpred(1),props(nprops),coords(3),         &
                drot(3,3),dfgrd0(3,3),dfgrd1(3,3)


    !*******************************************************************************
    ! 材料参数
    integer :: n_pt                ! 硬化曲线的数据点个数
    real(8) :: hard_data(int((nprops-2)/2),2)   ! 硬化曲线的数据点表格
    real(8) :: E,nu
    real(8) :: mu,kappa
    


    ! 从props数组中读取材料参数
    n_pt = int((nprops-2)/2)
    E = props(1)
    nu = props(2)
    j=3
    do i = 1, n_pt
        hard_data(i,1) = props(j)
        hard_data(i,2) = props(j+1)
        j = j + 2
    enddo


    ! 更新应力，状态变量以及一致性切线刚度模量
    mu = E / (1.0 + nu) / 2.0
    kappa = E / (1.0 - 2.0*nu) / 3.0
    call plastic_iso_umat(mu,kappa, n_pt,hard_data, stran,dstran, stress,statev,ddsdde)


    return
end subroutine UMAT

umat所需的支持函数编写于单独的module中（plastic_iso_pack.f90）用于调用，该方式可以使得主程序十分简洁。

4 测试

4.1 一个单元单轴加卸载试验

对一个单元进行单轴的加卸载试验，绘制应力应变滞回曲线。Abaqus设置的材料参数为，弹性部分的性质：

塑性部分的性质：

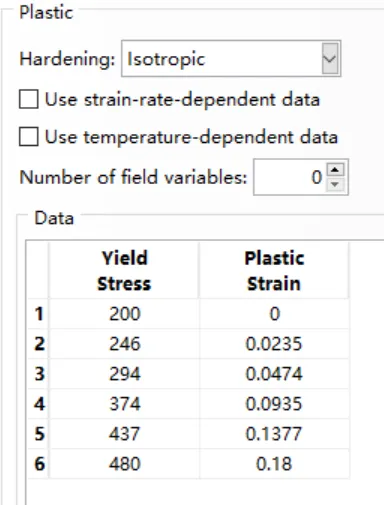
umat设置相同的材料参数为：

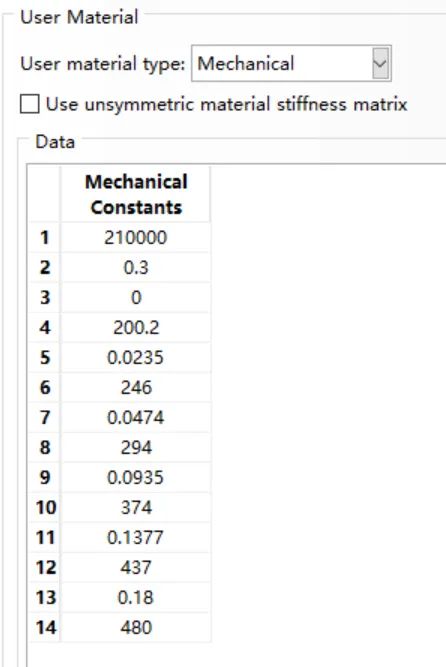
以及需要设置状态变量的个数为8。二者计算的结果对比如下：

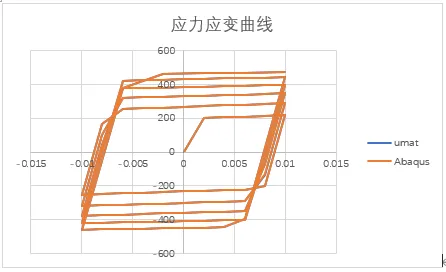
二者等效塑性应变的演化对比图如下：

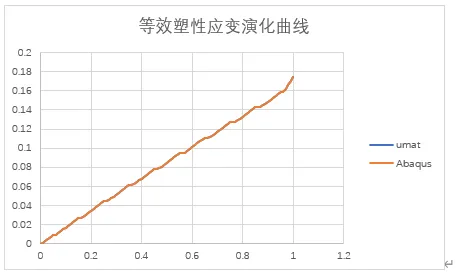
二者塑性耗散的演化对比图为：

4.2 带孔板拉伸实验

利用相同的材料性质计算一带孔板的拉伸实验。Abaqus计算的结果如下：

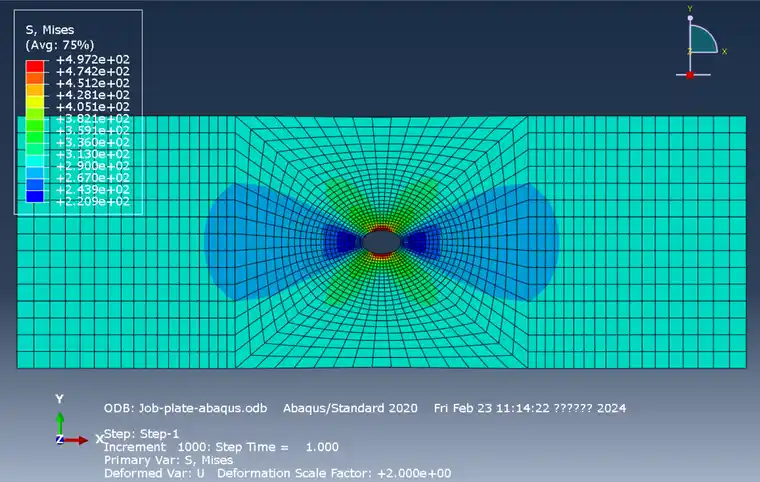
使用umat计算的结果如下：

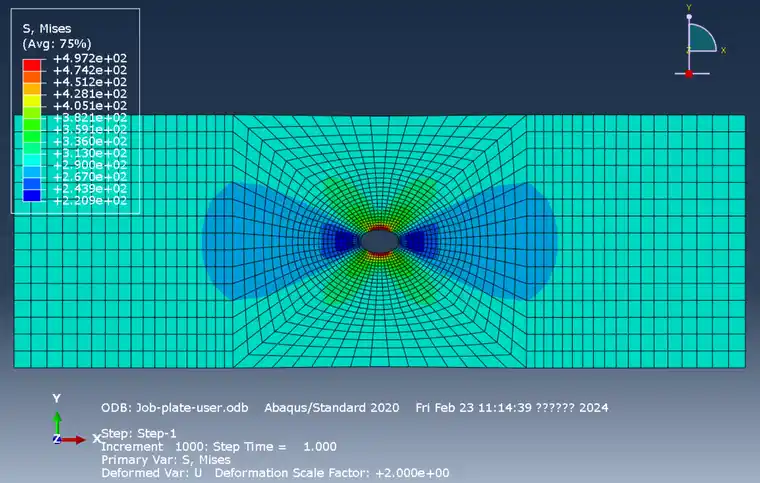
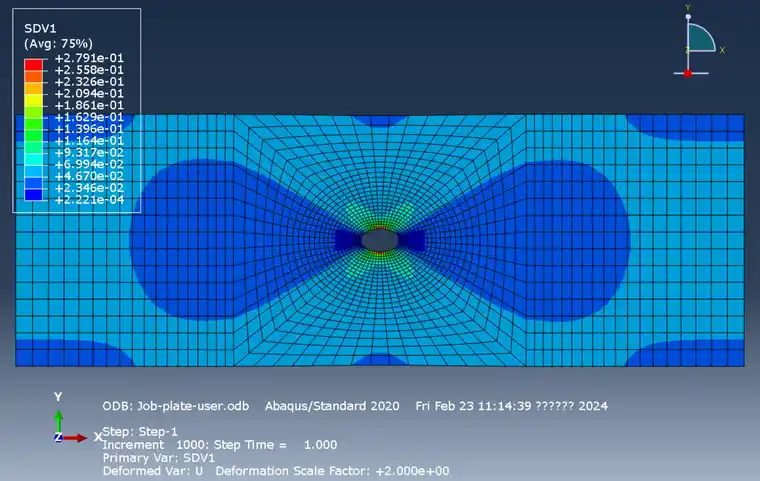
可看到二者的结果是完全相同的。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删