产品
一、前述
ANN人工神经网络有两个或两个以上隐藏层,称为DNN
只有一个隐藏层是多层感知机
没有隐藏层是感知机
二、反向传播应用举例
举例:
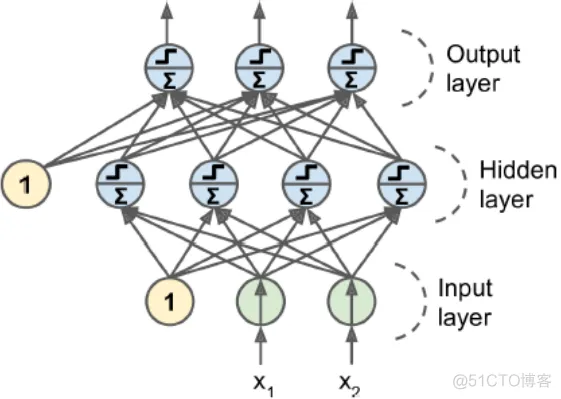
正向传播,反向传播是一次迭代,
正向传播:在开始的每一层上都有一个参数值w,初始的时候是随机的,前向带入的是每一个样本值。
反向传播:然后反过来求所有的梯度值。如果是BGD则再根据公式wt=wt-1-ag进行调整所有w值。
然后再正向传播,迭代,以此类推。
softmax通常用于最后一层的激活函数
前面层用relu函数
三、激活函数之Relu
公式:

解释:
Rectified Linear Units
ReLU计算线性函数为非线性,如果大于0就是结果,否则就是0
生物神经元的反应看起来其实很像Sigmoid激活函数,所有专家在Sigmoid上卡了很长时间,但是后
来发现ReLU才更适合人工神经网络,这是一个模拟生物的误解
如果w为0,反过来梯度下降求导的时候每根线上的梯度都一样。
代码:
import tensorflow as tfdef relu(X): w_shape = (int(X.get_shape()[1]), 1)
w = tf.Variable(tf.random_uniform(w_shape), name='weights') b = tf.Variable(0.0, name='bias')
z = tf.add(tf.matmul(X, w), b, name='z') return tf.maximum(z, 0., name='relu')n_features = 3X = tf
.placeholder(tf.float32, shape=(None, n_features), name='X')relus = [relu(X) for i in range(5)]
#list生成器output = tf.add_n(relus, name='output')#将集合中的元素加和在一起init = tf
.global_variables_initializer()with tf.Session() as sess: sess.run(init) result = output
.eval(feed_dict={X: [[1, 2, 3], [4, 5, 6], [7, 8, 9]]})#把里面placehoder的值传进来
print(result)1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.
四、激活函数和导数

五、DNN代码
import tensorflow as tffrom tensorflow.examples.tutorials.mnist import input_dataimport
numpy as npfrom tensorflow.contrib.layers import fully_connected
# 构建图阶段n_inputs = 28*28#输入节点n_hidden1 = 300
#第一个隐藏层300个节点 对第一个隐藏层前面有784*300跟线去算n_hidden2 = 100
#第二个隐藏层100个节点 对第二个隐藏层300*300根线n_outputs = 10
#输出节点X = tf.placeholder(tf.float32, shape=(None, n_inputs), name='X')y = tf
.placeholder(tf.int64, shape=(None), name='y')#自己手写的实现逻辑
# 构建神经网络层,我们这里两个隐藏层,基本一样,除了输入inputs到每个神经元的连接不同
# 和神经元个数不同# 输出层也非常相似,只是激活函数从ReLU变成了Softmax而已
# def neuron_layer(X, n_neurons, name, activation=None):
# X是输入,n_neurons是这一层神经元个数,当前隐藏层名称,最后一个参数是加不加激活函数#
# 包含所有计算节点对于这一层,name_scope可写可不写# with tf.name_scope(name):#with让代码看起来更加优雅一些#
# 取输入矩阵的维度作为层的输入连接个数# n_inputs = int(X.get_shape()[1])
# stddev = 2 / np.sqrt(n_inputs)#求标准方差#
# 这层里面的w可以看成是二维数组,每个神经元对于一组w参数#
# truncated normal distribution(调整后的正态分布) 比 regular normal distribution(正态分布)的值小#
# 不会出现任何大的权重值,确保慢慢的稳健的训练# # 使用这种标准方差会让收敛快#
# w参数需要随机,不能为0,否则输出为0,最后调整都是一个幅度没意义#
init = tf.truncated_normal((n_inputs, n_neurons), stddev=stddev)#把初始参数随机出来,比较小,
不会出现大的权重值
# w = tf.Variable(init, name='weights')
# b = tf.Variable(tf.zeros([n_neurons]), name='biases')
#b可以全为0# # 向量表达的使用比一条一条加和要高效# z = tf.matmul(X, w) + b
# if activation == "relu":# return tf.nn.relu(z)# else:
# return z#自己手写的实现逻辑'''with tf.name_scope("dnn"):
hidden1 = neuron_layer(X, n_hidden1, "hidden1", activation="relu")
hidden2 = neuron_layer(hidden1, n_hidden2, "hidden2", activation="relu")
# 进入到softmax之前的结果 logits = neuron_layer(hidden2, n_outputs, "outputs")'''
#用Tensorflow封装的函数with tf.name_scope("dnn"):
# tensorflow使用这个函数帮助我们使用合适的初始化w和b的策略,默认使用ReLU激活函数
hidden1 = fully_connected(X, n_hidden1, scope="hidden1")#构建第一层隐藏层 全连接
hidden2 = fully_connected(hidden1, n_hidden2, scope="hidden2")#构建第二层隐藏层 全连接
logits = fully_connected(hidden2, n_outputs, scope="outputs", activation_fn=None)
#构建输出层 #注意输出层激活函数不需要with tf.name_scope("loss"):
# 定义交叉熵损失函数,并且求个样本平均 # 函数等价于先使用softmax损失函数,再接着计算交叉熵,并且更有效率
# 类似的softmax_cross_entropy_with_logits只会给one-hot编码,我们使用的会给0-9分类号
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y, logits=logits)#封装好了损失函数
#把真实的Y值做onehot编码 loss = tf.reduce_mean(xentropy, name="loss")#求平均learning_rate = 0.01with tf
.name_scope("train"): optimizer = tf.train.GradientDescentOptimizer(learning_rate)#创建梯度下降的优化器
training_op = optimizer.minimize(loss)#最小化损失with tf.name_scope("eval"):#评估
# 获取logits里面最大的那1位和y比较类别好是否相同,返回True或者False一组值
correct = tf.nn.in_top_k(logits, y, 1)#logits返回是类别号 y也是类别号
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))
#转成1.0 0.0init = tf.global_variables_initializer()saver = tf.train.Saver()
# 计算图阶段mnist = input_data.read_data_sets("MNIST_data_bak/")n_epochs = 400
#运行400次batch_size = 50 #每一批次运行50个with tf.Session() as sess: init.run()
for epoch in range(n_epochs): for iterationo in range(mnist.train.num_examples//batch_size):
#总共多少条/批次大小 X_batch, y_batch = mnist.train.next_batch(batch_size)
#每次传取一小批次数据 sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
#传递参数 acc_train = accuracy.eval(feed_dict={X: X_batch, y: y_batch})
#每运行一次 看训练集准确率 acc_test = accuracy.eval(feed_dict={X: mnist.test.images,
#每运行一次 看测试集准确率 y: mnist.test.labels})
print(epoch, "Train accuracy:", acc_train, "Test accuracy:", acc_test)
save_path = saver.save(sess, "./my_dnn_model_final.ckpt")
# 使用模型预测with tf.Session as sess: saver.restore(sess, "./my_dnn_model_final.ckpt")
X_new_scaled = [...] Z = logits.eval(feed_dict={X: X_new_scaled}) y_pred = np.argmax(Z, axis=1)
# 查看最大的类别是哪个1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.
32.33.34.35.36.37.38.39.40.41.42.43.44.45.46.47.48.49.50.51.52.53.54.55.56.57.58.59.60.61.62.63.64.65.66.
67.68.69.70.71.72.73.74.75.76.77.78.79.80.81.82.83.84.85.86.87.88.89.90.91.92.93.94.95.96.97.98.99.100.

免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删