MASHIII调制器建模与仿真：Simulink实现

1.软件版本

MATLAB2021a

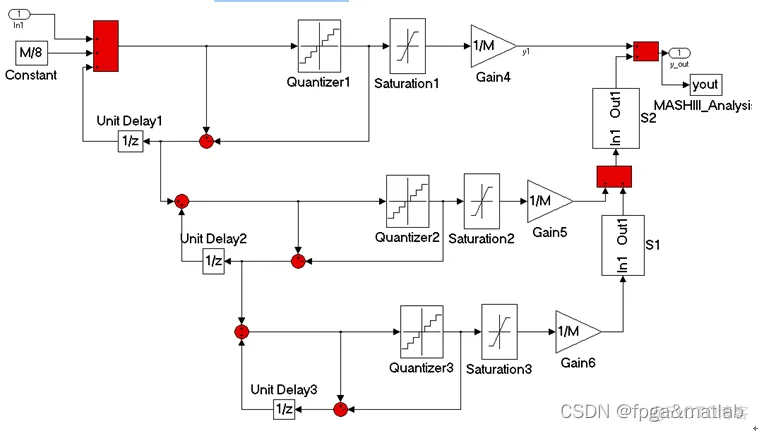
2.本算法理论知识

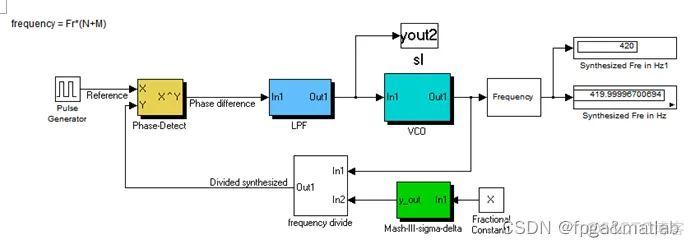
       这里，基于小数分频的频率合成器，考虑到你需要实现sigma-delta以及mash等结构。因此，系统的模块结构如下图所示：

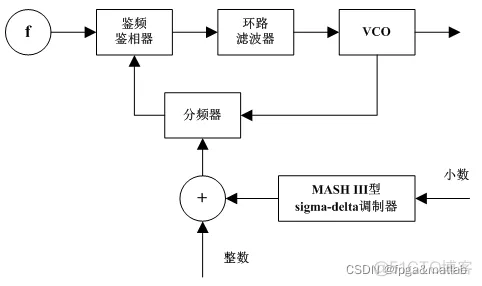
下面，我们对这个结构图进行SIMULINK建模。

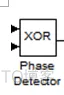
1.鉴相器采用XOR模块设计。

2.环路滤波器结构如下：

这里通过一个低通滤波器进行设计。

3.压控振荡器的设计，

上述几个模块都是可以通过现成的模块进行搭建，

3.核心代码

登录后复制

clc;close all;warning off;window  = hann(length(yout));
[Pyy,w] = periodogram(yout,window,100000);PSD2    = 1/M+1/100*(2*(w)).^4;
Len     = length(PSD2);%%%%%%%%%%%%%%%%%%figure;
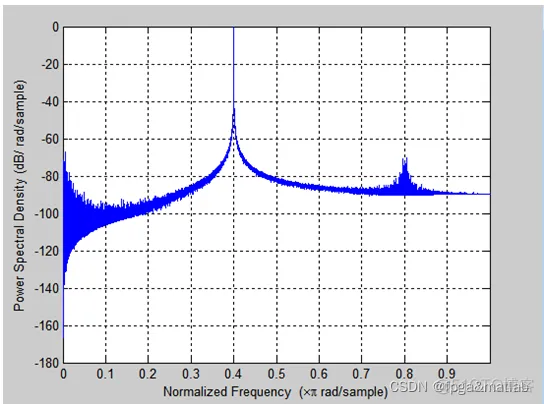
semilogx(w/pi,10*log10(pi*Pyy),'b');
holdsemilogx(w(Len/100:Len)/pi,10*log10(PSD2(Len/100:Len)),'k','linewidth',2);
grid onxlabel('Normalized Frequency (x\pi rad/sample)')ylabel('Power/frequency(dB/rad/sample)');
figure;plot(yout,'linewidth',2);grid on;xlabel('times');ylabel('sigmadelta调制器输出');
grid onfigure;hist(yout,5)xlabel('output yout')ylabel('number of occurance');figure;
plot(yout2(1:3*Len/4),'linewidth',2);grid on;xlabel('times');ylabel('V');
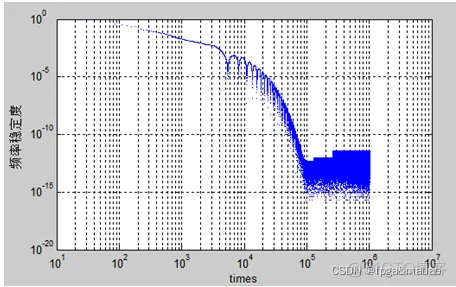
分析频率稳定度Fre = yout3;K   = 1;t1  = yout3(1:end-K);t2  = yout3(K+1:end);
Err = abs(t1-t2)./t1;figure;loglog(Err,'linewidth',2);grid on;xlabel('times');
ylabel('频率稳定度');%%%最后进行杂散分析N        = 16;             %累加器的位数；K        = fix((2^N)*0.2); 
%频率控制字，即累加的步长；D        = 8;             %8bit DACg        = gcd(K,2^N);pe       = 2^N/(g);
n        = 1:pe;pp       = pe+1;          %频谱分析点数add_y    = mod(n*K,2^N);  %累加器的输出表达式；
%设定量化区间pat             = -1 + 1/ (2^ (D - 1) ):1/ (2^ (D - 1) ):1 - 1/ (2^ (D -1) ); 
%设定量化码本值codebook        = -1 + 1/ (2^D):1/ (2^(D - 1) ) :1 - 1/ (2^D); 
rom_x           = cos(2*pi*add_y/(2^N));[index,quants2] = quantiz(rom_x,pat,codebook);
[Pzz,wz]        = periodogram(quants2,[],'onesided',pp);figure; psdplot(Pzz/max(Pzz),wz);
1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.36.37.
38.39.40.41.42.43.44.45.46.47.48.49.50.51.52.53.54.55.56.57.58.59.60.61.62.63.64.65.66.67.68.69.70.71.72.
73.74.75.76.77.

4.操作步骤与仿真结论

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删