转速反馈单闭环直流调速系统仿真

直流电机模型框图如下图所示，仿真参数为R=0.6，Tl=0.00833，Tm=0.045，Ce=0.1925。本次仿真采用算法为ode45，仿真时间5s。

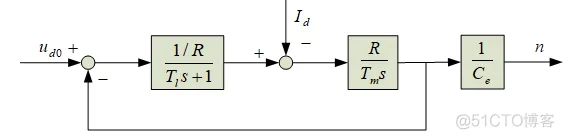
图1 直流电机模型

1、开环仿真：

用simulink实现上述直流电机模型，直流电压Ud0取220V，

0~2.5s，电机空载，即Id=0；

2.5s~5s，电机满载，即Id=55A。

画出转速n的波形，根据仿真结果求出空载和负载时的转速n以及静差率s。改变仿真算法，观察效果（运算时间、精度等）。

仿真模型图为：

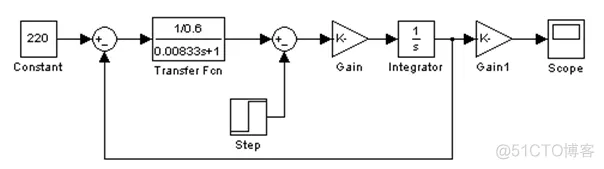
    示波器所示转速波形为：

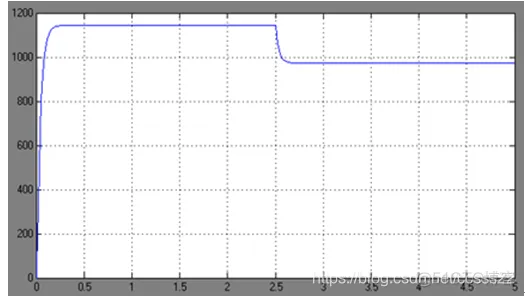
读图知：空载时转速n=1143r/min，负载时转速n=971r/min，静差率s=15.048%

     改变仿真算法：

     ①ode23                         ②ode113

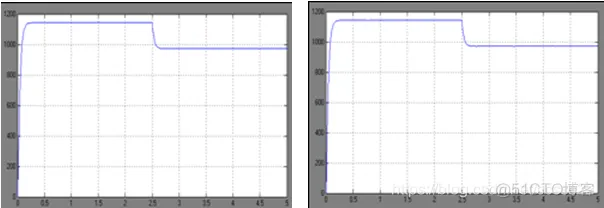
     ③ode15s                        ④ode23s

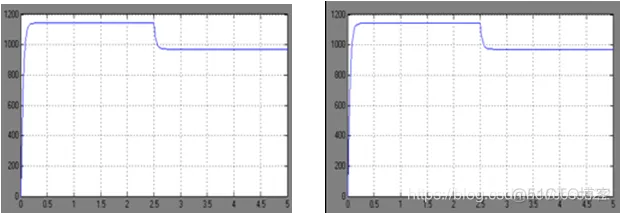
     ⑤ode23t                        ⑥ode23tb

 
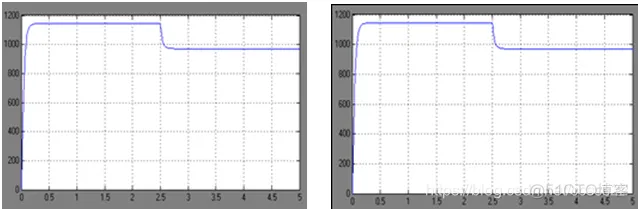
改变仿真算法，转速波形基本没有发生变化。

2、闭环仿真：

在上述仿真基础上，添加转速闭环控制器，转速指令为1130rpm，

0~2.5s，电机空载，即Id=0；

2.5s~5s，电机满载，即Id=55A。

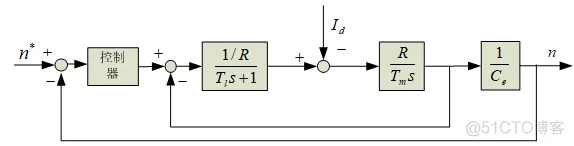
图2 转速闭环直流电机调速控制框图

控制器为比例环节：试取不同kp值，画出转速波形，求稳态时n和s并进行比较。

仿真模型图为：

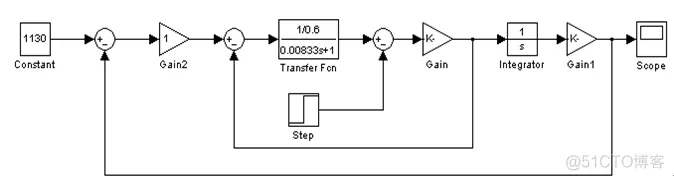
示波器所示转速波形为：

  ①Kp=0.5

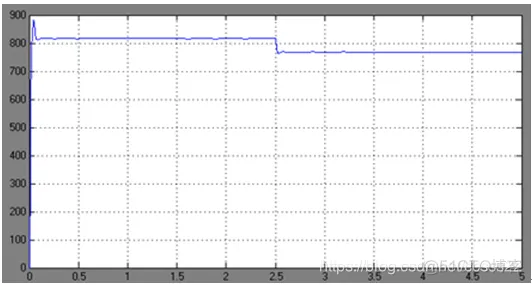
  空载转速n=816r/min，稳态时转速n=768r/min，静差率s=5.88%

  ②Kp=1

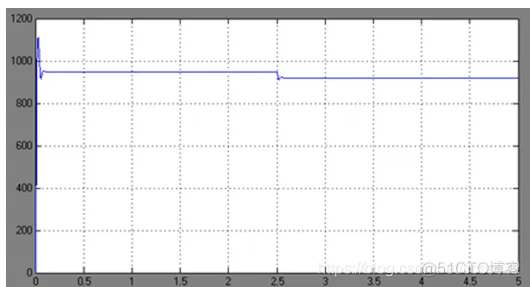
空载转速n=948r/min，稳态时转速n=920r/min，静差率s=2.95%

(2)控制器为比例积分环节，设计恰当的kp和kI值，并与其它不同的kp和kI值比较，画出不同控制参数下的转速波形，比较静差率、超调量、响应时间和抗扰性。

   仿真模型图为：

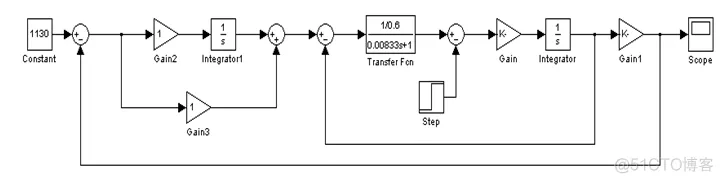
示波器所示转速波形为：

① Kp=1，Ki=1

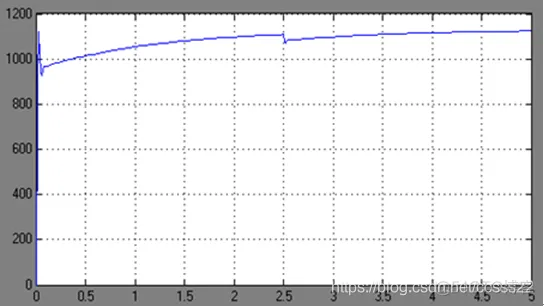
在仿真时间内并未达到稳定状态，有超调量

② Kp=1，Ki=5

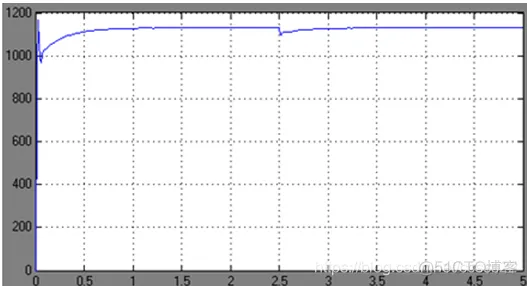
空载转速n=1130r/min，稳态时转速n=1130r/min，静差率s=0，超调量=3.54%

闭环反馈控制系统是按被调量的偏差进行控制的系统，只要被调量出现偏差，它就会自动产生纠正偏差的作用。而转速降落正是由负载引起的转速偏差，显然，闭环调速系统应该能大大减少转速降落。

1）控制器为比例环节时

由实验波形可知，Kp值越大，稳定后的转速n就越大，超调量也越大，静差率s则越小。静差率s反映的是闭环反馈效果，s越小，闭环反馈效果则越好，即Kp值越大，闭环反馈效果则越好。在实际中，我们希望得到的是超调量小（即希望Kp小）和闭环反馈效果好（即希望Kp大）的系统，但是这二者却是相互矛盾的，我们只能从中选取一组最优平衡值，使得在较小超调量和较好反馈控制下系统能够最大限度的最好工作。

2）控制器为比例积分环节时

超调量和响应时间受Kp、Ki共同控制，在相同Kp下，Ki越大，上升速度越快，响应时间越短，超调量越大；在相同Ki下， Kp越大，上升速度越快，响应时间越短，超调量越大。即Kp*Ki的值越大，上升速度越快，响应时间越短，但是超调量越大（Kp小于1时无超调量）。

静差率在仿真时间内为0，即实现了无静差调速系统。

当Kp取一定值时，Ki的值在增大到一定程度时，会产生振荡发散现象。

比较开环系统与闭环系统知，开环调速系统受到外界的干扰信号影响较闭环调速系统大；闭环系统的静差率比开环系统的小，且带比例放大器的反馈控制闭环调速系统是有静差的调速系统，而采用比例积分调节器的闭环调速系统则基本上实现了无静差调速，闭环反馈效果较好。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删