ANSYS模型降阶技术：Model Order Reduction解析

最近在做一些Fast simulation的工作，用到了Model Order Reduction (MOR),觉得十分有用，在这里推荐给大家，并且附上ANSYS 和Matlab的source code.现在最流行的MOR主要基于Krylov subspace projection method, 基本原理如下：
 

假设原来的linear system model的node数是N (NxN的矩阵）, N ~ 100000, 我们可以创建一个N x r 的矩阵，把原来NxN的矩阵project到 r x r的矩阵上去 (r<<N)，这样求解过程可以在这个小矩阵上完成，然后再把结果project回到原来的NxN的矩阵空间上去。
 

以下是源程序介绍：

1) Example.mac: ANSYS mac file 用来建立一个三维的热传导模型，并加上载荷。用户必需设置文件里的SOLVE_OPTION变量。
 
取0时，输出模型的heat capacitance 和 heat conductance 矩阵(用HBMAT commands)，分别保存到C_File.dat和K_file.dat（Thermal load 也保存到K_File.dat）。
 

取1和2时分别做steady-state和transient simulation。
 
2) MOR_ODE.m: matlab 程序，读取K_File.dat和C_file.dat进行MOR,并且和ANSYS 结果（ansys.dat,在Example.mac里SOLVE_OPTION＝2）的对比。用户必需设置Solver_Option = 1调用matlab的lu分解函数。（Solver_Option = 0 是使用external 的 MOR_MUMPS.exe程序做matrix factorization,速度可提高数倍。MOR_MUMPS.exe是自己写的C语言程序，用到了GNU MUMPS linear solver library和BLAS library, 需用GNU fortran 和 gcc 编译).
 

ANSYS模型的MOR步骤：

1): 在ANSYS里建模，mesh,以及加载 （不必求解）。

2): 用HBMAT命令输出system matrice文件(Example.mac里有对应的code).

3): 在Matlab里读入system matrice文件进行MOR(code在MOR_ODE.m里).

4): 在Matlab里用ODE solver求解并project solution back 得到原模型上的解。
 
限制： 模型必需是linear system response model.
 
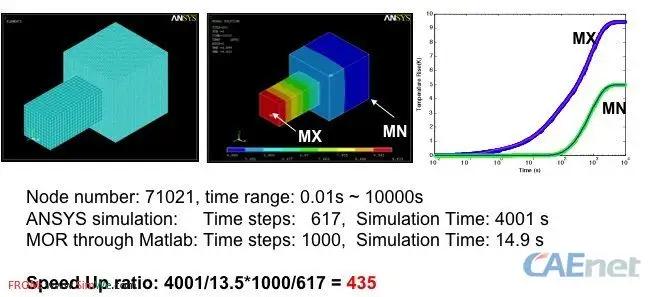
ansys.dat 中包含了用ANSYS得到的MX和MN点的温度变化曲线， 用来和MOR结果做比较。
 

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删