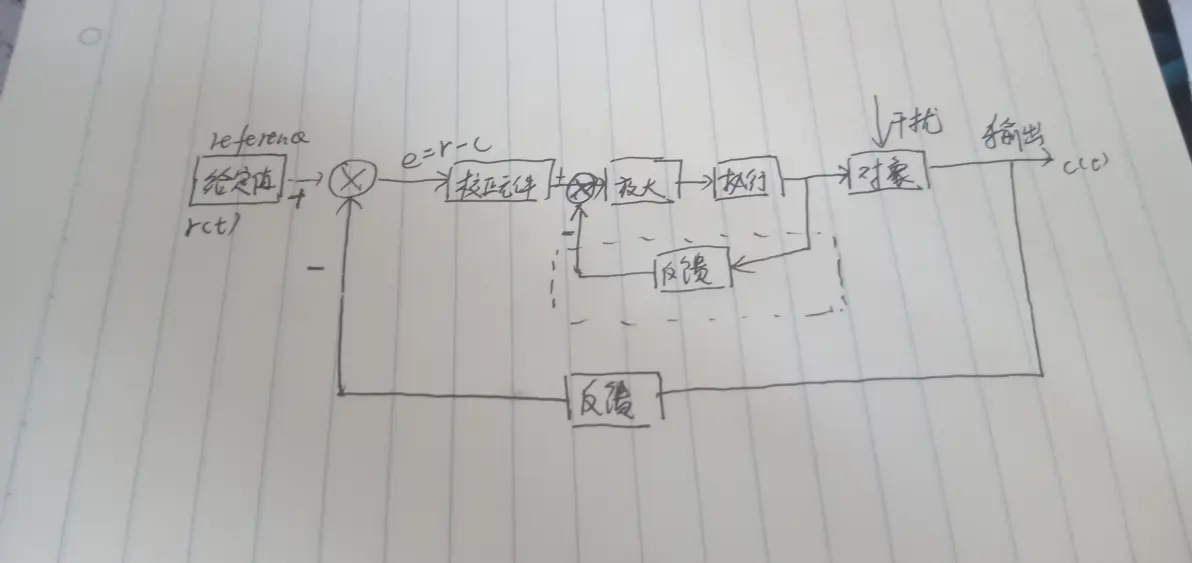
闭环控制
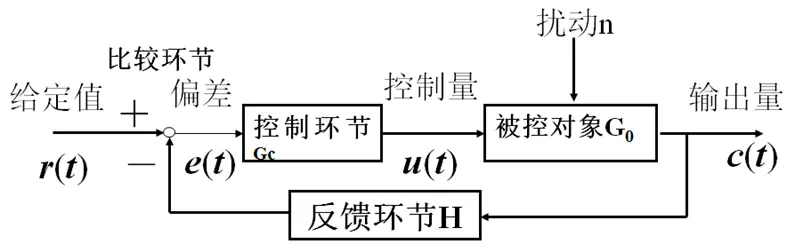
控制系统的基本要求
1.稳(基本要求)
要求系统基本稳定
2.准(稳态要求)
系统响应达到稳时,输出精度要高
3.快(动态要求)
系统阶跃响应的过渡过程,要快速
控制系统的数学模型

两种建模方法
通常我们需要建立输出与输入的微分方程模型,而且有时候还需要将非线性系统线性化。
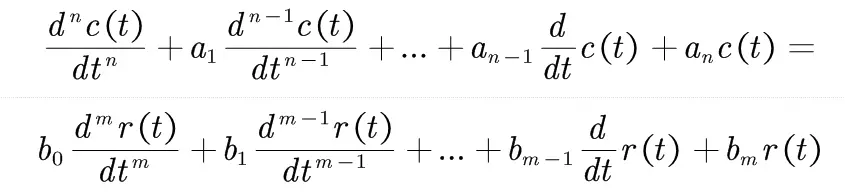
线性化函数的各阶导数要存在
输入量的变化范围不能太大
传递函数
零初始条件下,线性定常系统的输出与输入的拉普拉斯变换之比
传递函数只与系统的结构和内部的参数有关
在单位冲激响应作用下,系统的输出的拉氏变换即为传递函数
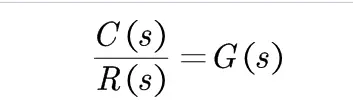
传递函数
几种常见的传递函数模型
1.直接用分子分母多项式

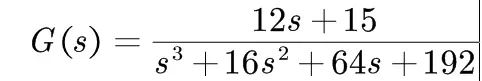

第二种方法为定义laplace算子
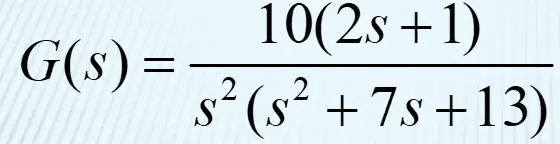
传递函数越复杂,可以尝试用拉氏算子来定义,也可以用多项式乘法conv

以上为连续时间系统
对于离散系统,可以直接设置采样时间
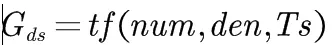
也可以设置延时
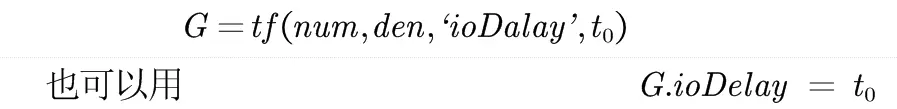
可以tfdata获得传递函数的分母与分子多项式
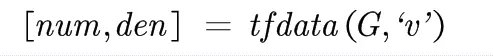

同样也可以用结构体索引,参见下面的get函数

可以用get获取传递函数的参数

显然,我们可以用结构数组(点访问)或者用set来修改,或者定义时给出
例如

结构数组
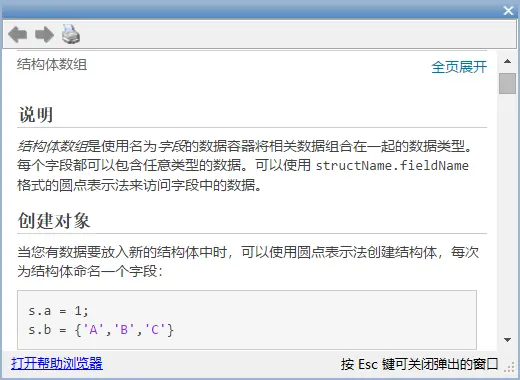

set

定义时给出
2.零极点增益(zero-pole-gain)模型

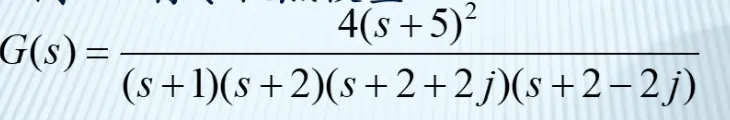

同样,也可以定义拉氏算子

绘制零极点分布图
[zeros,poles] = pzmap(sys) ,得到零点和极点值
无返回参数时画出零极点坐标图
pzmap(sys)

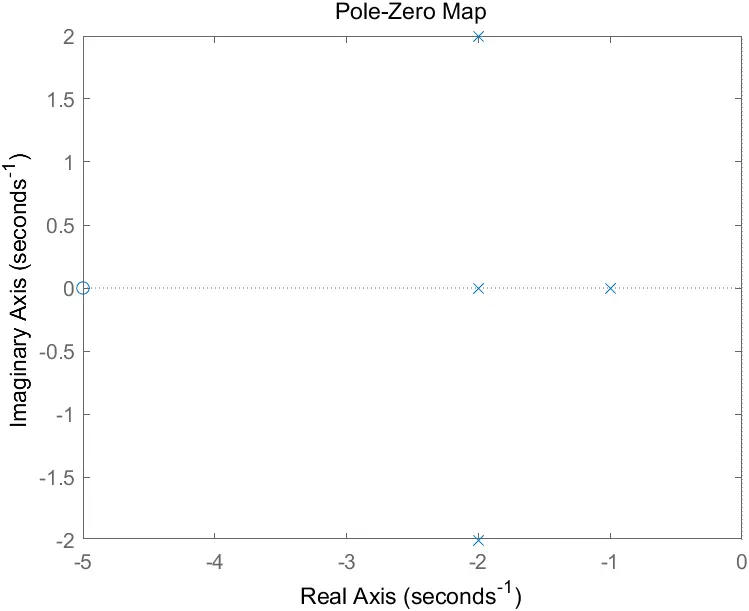
pzmap
3.状态空间( state space model)函数模型

确定A、B、C、D四个矩阵,建立状态空间函数模型
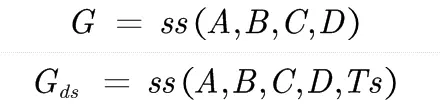

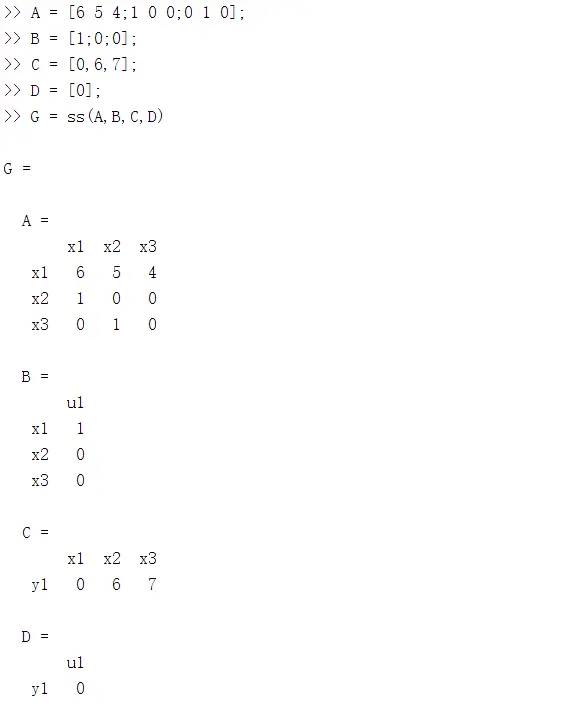
得到系统的所有参数get(G)

也可以用ssdata查看系统参数

也可以用结构体数组点访问


几种不同模型的转换
传递函数 tf
零极点增益 zpk
状态函数 ss
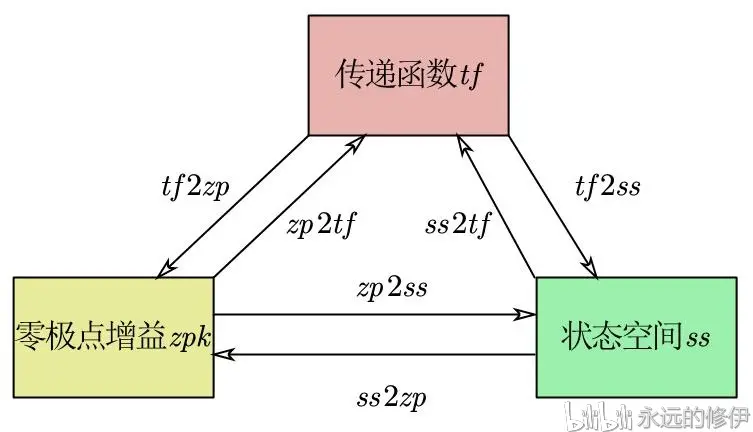
转换图
第一类函数
传入的参数是系统,直接转换为目标模型
第一类函数(把其它类型的模型转换为函数表示的模型自身)

eg.
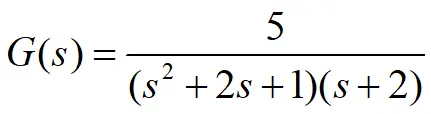


第二类函数 将本类型传递函数参数转换为其它类型传递函数参数
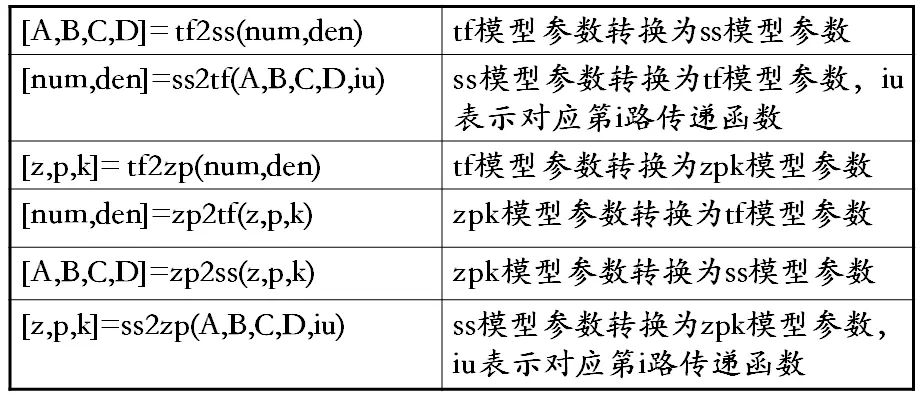
注意这里是zp
eg.





无限套娃。