计算特征重要性的原理在随机森林算法中使用的指标和方法上有所不同。下面我将解释两种常见的特征重要性度量方法:
(1)基于袋外误差减少(Out-of-Bag Error Reduction):在随机森林中,每个决策树都是通过从原始数据集中进行有放回抽样(bootstrap)来构建的。这意味着对于每个决策树,大约有约三分之一的数据样本不会在构建该树时使用,这些样本被称为"袋外样本"(Out-of-Bag, OOB)。特征重要性度量可以通过计算在袋外样本上预测误差的减少来进行。方法是对于每个决策树,在袋外样本上计算预测误差(例如,均方误差)并记录下来。然后,随机打乱某个特征的值在袋外样本上进行预测,并重新计算预测误差。特征重要性度量即为原始预测误差和打乱后的预测误差之差的平均值。
(2)基于特征贡献度(Gini Importance):该方法使用基尼指数(Gini Index)作为特征重要性的度量。对于每个决策树,计算每个特征在分裂节点上的基尼指数。基尼指数衡量了在给定节点上根据特征进行分割后,样本在类别上的不纯度。特征重要性度量即为每个特征的基尼指数之和,并进行归一化。
这些方法都基于决策树的构建和分裂过程,通过比较特征对模型的预测准确性和不纯度的影响程度来衡量特征的重要性。需要注意的是,不同的方法可能在计算上有细微的差异,因此具体实现和算法细节可能会有所不同
matlab基于OOB计算重要性
1:对于随机森林中的每一颗决策树,使用相应的OOB(袋外数据)数据来计算它的袋外数据误差,记为errOOB1.
2: 随机地对袋外数据OOB所有样本的特征X加入噪声干扰(就可以随机的改变样本在特征X处的值),再次计算它的袋外数据误差,记为errOOB2.
3:假设随机森林中有Ntree棵树,那么对于特征X的重要性=∑(errOOB2-errOOB1)/Ntree,之所以可以用这个表达式来作为相应特征的重要性的度量值是因为:若给某个特征随机加入噪声之后,袋外的准确率大幅度降低,则说明这个特征对于样本的分类结果影响很大,也就是说它的重要程度比较高。
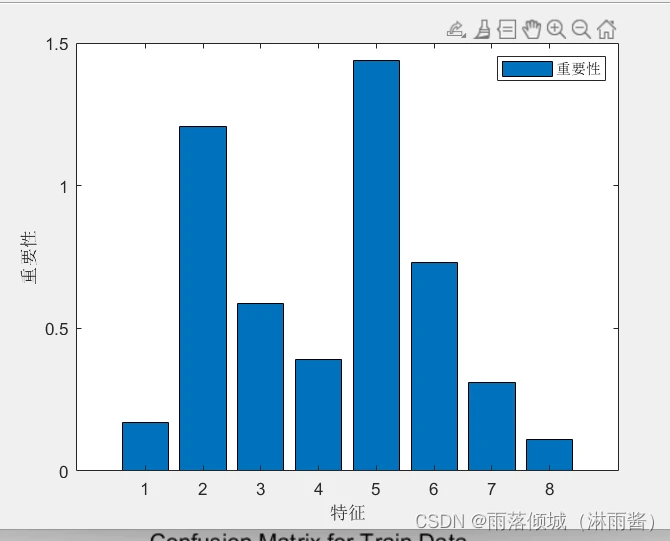
代码:
importance = net.OOBPermutedPredictorDeltaError; % 重要性
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删