在数值模拟中,如何有效处理固体壁面附近的流场一直是一个比较棘手的问题。一个稍复杂一点算例,简单更换一下壁面处理方法对计算结果都有较显著的影响,在缺少实验数据验证和流场涉及多种流动形态时,如何选择行之有效和经济合理的算法是一个艰难的考验,一般需要仔细考察流场与算法机理之间的契合度。
边界层分为层流边界层和湍流边界层,层流边界层为最靠近壁面或者层流流动时的边界层,对于一般湍流流动,两种边界层都有。按参数分布规律划分时,边界层分为内区和外区,内区分为:
粘性底层,Laminar sublayer(y+<5,Amano的三层模型),粘性起主导作用,在粘性支层中与壁面平行的速度与离开壁面的距离成线性关系(陶文铨,《数值传热学》);
过渡层,Buffer region(5<y+<30),湍流作用与粘性作用共同作用;
对数律层,Log-law region(30<y+),湍流起主导作用,无量纲速度与温度分布服从对数分布律;
外区:惯性力主导,上限取决于雷诺数
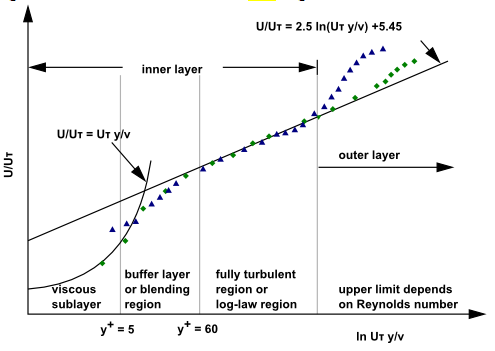
图1 边界层结构(引自中科大Fluent讲稿)
FLUENT中有两种方法处理近壁面区域:
A.壁面函数法。
不求解粘性影响内部区域(粘性子层及过渡层),使用一种称之为“wall function”的半经验方法去计算壁面与充分发展湍流区域之间的粘性影响区域。采用壁面函数法,省去了为壁面的存在而修改湍流模型。Fluent中的standard wall functions, scalable wall functions, Non-Equilibrium wall functions和Enhanced wall treatment都属于壁面函数法的模型。
B.近壁模型法。
修改湍流模型以使其能够求解近壁粘性影响区域,包括粘性底层。此处使用的方法即近壁模型。(近壁模型不需要使用壁面函数,如一些低雷诺数模型,K-W湍流模型是一种典型的近壁湍流模型)。
所有壁面函数(除scalable壁面函数外)的最主要缺点在于:沿壁面法向细化网格时,会导致数值结果恶化。当y+小于15时,将会在壁面剪切力及热传递方面逐渐导致产生无界错误。然而这是若干年前的工业标准,如今ANSYS FLUENT采取了措施提供了更高级的壁面格式,以允许网格细化而不产生结果恶化。而y+无关的格式是默认的基于w方程的低湍流模型,其采用网格求解的方式计算近壁面粘性区域。对于基于epsilon方程的模型,增强壁面函数(EWT)提供了相同的功能。这一选项同样是SA模型所默认的,该选项允许用户使其模型与近壁面y+求解无关。
只有当所有的边界层求解都达到要求了才可能获得高质量的壁面边界层数值计算结果。这一要求比单纯的几个Y+值达到要求更重要。
使用近壁模型法时,覆盖边界层的最小网格数量在 10层左右,最好能达到20层。还有一点需要注意的是,提高边界层求解常常可以取得稳健的数值计算结果,因为只需要细化壁面法向方向网格。
对于非结构网格,建议划分10~20层棱柱层网格以提高壁面边界层的预测精度。棱柱层厚度应当被设计为保证有15层或更多网格节点。另外,棱柱层大于边界层厚度是必要的,否则棱柱层会限制边界层的增长。这可以在获得计算结果后,通过查看边界层中心的最大湍流粘度,该值提供了边界层的厚度(最大值的两倍位置即边界层的边)。
一些建议:
1)对于epsilon方程,使用enhanced壁面函数。
2)若壁面函数有助于epsilon方程,则可以使用scalable壁面函数。
3)对于基于w方程的模型,使用默认的增强壁面函数。
4)SA模型,使用增强壁面处理。
1、Standard wall functions
ANSYS FLUENT中的标准壁面函数是基于launder与spalding的工作,在工业上有广泛的应用。
对于标准壁面函数法,在划分网格时,把第一个内节点P布置到对数分布律成立的范围内,即配置到旺盛湍流区域。通常,在y+>30~60的区域,平均速度满足对数率分布。在FLUENT程序中,这一条件改变为y+>11.225。当网格y+<11.225时,FLUENT中采用层流应力应变关系,即:U+=Y+。
对于对一层网格所在的y+值,各个学者推荐的范围是不一样的,但一般在30-60之内肯定是没有问题的。也有推荐10-110甚至200的。y+的值合理,意味着你的第一层边界网格布置比较合理,如果y+不合理,就要调整你的边界层网格。y+普遍存在于湍流问题中,Y+是由solver解出來的結果,网格划分时,底层网格一般布置到对数分布律成立的范围内,即11.5~30<=y+<=200~400。在计算开始时,y+并不知道,这些值需要在计算过程中加以调整。数值计算实践表明,y+对传热特性的影响比较大,往往存在一个合适的取值范围,在该范围内数值计算结果与实验数据的符合较好。算每个模型都要先大概算一下,然后得到y+,然后再算第一层高度,重新画网格,貌似像是一个迭代的过程。
根据雷诺相似,我们可以根据平均速度的对数分布,同样给出平均温度的类似分布。
FLUENT提供的平均温度壁面法则有两种:
1,导热占据主要地位的热导子层的线性率分布;
2,湍流影响超过导热影响的湍流区域的对数分布。
温度边界层中的热导子层厚度与动量边界层中的层流底层厚度通常都不相同,并且随流体介质种类变化而变化。例如,高普朗特数流体(油)的热导子层厚度比其粘性底层厚度小很多;对于低普朗特数的流体(液态金属)相反,热导子层厚度比粘性底层厚度大很多。
标准壁面函数用于以下模型:k-epsilon模型与Reynolds stress模型。这两个模型均为高雷诺数模型。
2、Scalable wall functions
该壁面函数是14.0新加的,以前的版本中没有。也是CFX软件中默认的湍流壁面函数。
该壁面函数能避免在y*<15时计算结果恶化,该壁面函数对于任意细化的网格,能给出一致的解。当网格粗化使y*>11时,该壁面函数的表现与标准壁面函数一致。
scalable壁面函数的目的在于联合使用标准壁面方法以强迫使用对数律。该功能是通过使用限制器y*=max(y*,y*limit)来实现的,其中y*limit=11.06。
3、Non-equilibrium wall functions
非平衡壁面函数的特点:
1)用于平均速度的launder及spalding的对数律对于压力梯度效应敏感。
2)采用双层概念以计算临壁面单元的湍流动能。对于平均温度及组分质量分数则与标准壁面函数处理方式相同。
非平衡壁面函数考虑了压力梯度效应,因此对于涉及到分离、再附着、及撞击等平均速度与压力梯度相关且变化迅速的复杂流动问题,推荐使用些壁面函数。但是非平衡壁面函数不适合于低雷诺流动问题。
非平衡壁面函数适用于高雷诺流动问题,适用于以下湍流模型:
1)K-epsilon模型;
2)Reynolds stress transport模型。
4、Enhanced wall treatment
不依赖于壁面法则,对于复杂流动尤其是低雷诺数流动问题很适合。该方法要求近壁面网格很密,y+接近于1,比low-Reynolds number model要求的网格更密。
对于epsilon方程的近壁面处理结合了速度分布双层模型和壁面增强处理函数。增强壁面处理使用传统的双层区域模型(整个计算域被划分为粘性影响区域和充分湍流区域)给边界层分区,然后给近壁单元指定湍流耗散率e和湍流粘度。增强型壁面函数的特点是用一个单一的壁面函数平滑地混合了对数层公式与层流公式,这样它的计算范围扩展到了全部近壁区域。
增强壁面函数可用于以下湍流模型:
1)所有的基于epsilon的湍流模型(不包括二次RSM模型)
2)所有的w模型
3)对于SA模型,这一选项不可用。然而,这一模型对于壁面函数(y*>15)及粘性子层网格(y*<2)是一致的。处于中间的网格应当被避免 ,因为会降低计算精度。换句话说,对于SA模型,要么y*>15,要么y*<2
壁面函数方法的局限
对于大多数壁面边界流动问题,标准壁面函数能给出合理的预测。非平衡壁面函数考虑了压力梯度效应,扩展了标准壁面函数的功能。但是一些流动问题不适合使用壁面函数,否则可能导致不合理的解。如以下一些情况:
1)低雷诺数流动或近壁面效应(例如小缝出流、高粘性低速流动问题)
2)通过壁面的大量沸腾
3)大的压力梯度导致的边界层分离
4)强体力(如旋转圆盘附近的流动、浮力驱动流动)
5)近壁区域高度三维流动(如ekman螺旋流动、高度歪斜的3D边界层)
若模型中出现了以上的情况,则必须使用近壁模型。ANSYS FLUENT中提供了增强壁面处理以应对这些情况。这一方法能够用于K-epsilon模型及RSM模型。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删