摘 要:基于珠链模型,采用离散单元法对纤维模型进行柔性化处理;通过搭建 EDEM-Fluent 耦合仿真模型,对柔性再生碳纤维在渐缩流场中的流动取向过程进行仿真模拟。采用湿法取向技术对 6 mm 纤维进行重新取向排布制备取向毡,将仿真结果与实验结果进行对比。采用模压法制备了碳纤维/环氧树脂基复合材料,对其力学性能进行表征。结果表明:在纤维跟随流体运动的过程中,纤维会受到轴向剪切力的作用,发生不同程度的弯曲变形,并沿着流体流动方向发生旋转,从而在移动过程中完成取向。利用二维方向张量对纤维毡取向度进行表征,其取向度为 98%;制备的取向复合材料弯曲强度和模量较未取向材料分别提升 70.6%和 88.5%。
关键词:纤维取向;柔性纤维;离散单元法;渐缩流场;力学性能
0 前言
碳纤维/环氧树脂基复合材料(CF/EP)在航空航天、风电、交通等大型承力构件制造中得到广泛应用[1],尤其在航空航天方面,常用来制造发动机壳体、蒙皮等重要部件,可以发挥碳纤维复合材料轻量化、高强度等优势[2]。随着碳纤维应用范围的不断扩大,各领域对碳纤维需求量急速增加,制造中的废弃边角料和服役期满碳纤维复材制品也随之增长[3]。对废弃碳纤维复合材料中的碳纤维进行回收再利用是解决碳纤维废弃物堆积问题的最佳途径,回收之后的再生碳纤维性能与原纤维相差无几,回收成本却远远小于生产成本[4]。回收碳纤维通常采用模压工艺实现复材制品成型,并应用于汽车外覆盖件等部位。但是碳纤维作为一种各向异性的材料,其轴向力学性能优于径向力学性能[5],随机排列的短纤维大大限制了其应用途径。因此,有效的纤维取向技术成为回收碳纤维大规模工业应用的关键技术之一。
目前一些学者对纤维取向技术进行了相关研究。TIMBRELL 等[6]在纤维表面涂覆铁粒子来制备得到磁性纤维,通过加入磁场实现纤维的取向排列;VAYAKARNAM 等[7]采用电场法对纤维进行取向,为了增强纤维的导电性在纤维表面涂覆导电材料,利用电场力的作用改变纤维的排列方向,其制备得到的取向纤维毡沿取向方向±20°内只有 70%左右的纤维。BAGG 等[8]通过湿法取向技术,使用高黏度分散介质对回收碳纤维进行分散处理,利用纤维溶液通过渐缩取向喷头时形成的剪切力改变纤维排列方向,提高了取向纤维毡的制备效率,制备的纤维毡沿取向方向±15°内有 90%的纤维;BRISTOL 大学[9]开发了一种独特的高性能非连续纤维排列方法,利用悬浮在非常稀薄的低黏度液体中纤维的动量变化来实现高质量的纤维对齐,成功生产出 67%的纤维排列在±3°范围内的拉伸试样;HUAN 等[10]让纤维悬浮液在重力作用下通过狭缝,狭缝壁区域产生的剪切流使纤维旋转至与流体流动方向一致,从而使制备的取向纤维毡中有 83.5%的纤维排列在±10°范围内。
相关研究表明,湿法取向技术制备的纤维取向毡有较高的取向度。但是,由于纤维直径小(5~10 μm),实验所用的纤维通常为短切纤维,其在流场中运动时的形态演化规律不清晰,难以观察纤维在流场中的取向变化。使用仿真工具能够直观呈现出纤维在流场内的运动规律。HE[11]采用了光滑粒子流体动力学模拟方法,针对刚性短纤维增强聚合物复合材料的三维注射成型流动,研究了注射成型过程中的填充细节和纤维取向;WU 等[12]提出了基于平滑粒子动力学和离散单元法耦合的综合粒子方法来预测离散短纤维的注射成型过程;周大鹏等[13]利用 EDEM-Fluent 耦合模型对喷砂喷嘴内气固两相的运动状态进行模拟,分析了喷嘴收缩角、喉部半径等因素对喷砂量的影响规律。
尽管有文献研究了流体中纤维的运动规律与取向状态,但是其针对的对象都是在流场中运动时不会发生形态变化的刚性纤维。而再生碳纤维往往是柔性纤维,其在流场内由于受到流体的剪切作用,形态上会发生弯曲扭转等变化。因此,本文采用仿真工具建立柔性纤维模型,通过搭建包含的纤维和流体的固液两相流 EDEM-Fluent 耦合数值模型,基于湿法取向技术对柔性短切碳纤维的流动取向过程进行仿真模拟,通过与实验结果对比验证取向模型的有效性;并搭建湿法取向移动平台对纤维进行取向排布,制备取向纤维毡,进一步研究 CF/EP 复合材料力学性能的提升效果。
1 实验设备与方法
自主搭建了湿法纤维取向工艺平台以制备取向纤维毡,如图 1 所示。取向装置由三轴移动平台、移动控制系统、气压控制系统、取向针筒、真空抽吸装置等组成。其中三轴移动平台由步进电机和皮带等组装而成;气压控制系统由空气压缩机和点胶机组成。

制备纤维悬浮液方法如下:向 1 L 烧杯中加入700 mL蒸馏水,称取10.5 g羟乙基纤维素倒入水中,使用双螺旋搅拌桨在 600 r/min 的搅拌速率下搅拌30 min,随后提升速率至 1 200 r/min 继续搅拌 6 h,期间缓慢加入 2.8 g 的回收碳纤维。搅拌至纤维溶液出现明显爬杆现象、溶液颜色均一且无明显团聚丝束时停止搅拌。将搅拌完全的纤维溶液放至真空箱内抽真空,去除因搅拌桨转动产生的大量气泡。制备完成的纤维悬浮液中,纤维呈无规则状态均匀分布在溶液里。将分散完全的纤维悬浮液倒入取向针筒,调节点胶机气压大小,调整针筒位置,设置喷头移动速度。纤维溶液在气压的作用下从渐缩针嘴中挤出,并且均匀铺层在滤网上。滤网下方放置真空抽吸装置(由抽滤瓶和真空泵等组成),抽滤瓶紧贴滤网沿着纤维排布方向移动,利用真空压力抽滤掉纤维溶液中的大部分水分和分散剂,得到潮湿纤维毡。干燥至质量恒定得到制备完成的取向纤维毡。
2 EDEM-Fluent 耦合模型
在湿法纤维取向工艺中,纤维在渐缩流场中通过液体提供的剪切力完成取向,但纤维在其中的运动过程和形态变化难以观察。因此,搭建包含纤维和流体的固液两相流模型,对该过程进行仿真模拟,研究柔性纤维在渐缩流场中的运动规律,对理解纤维的取向机制、提高纤维制品性能具有指导意义。
2.1 柔性纤维模型
再生碳纤维的固液两相流数值模拟中,为了在仿真模型中模拟柔性纤维、准确描述纤维在流场中的运动特性,本文基于 YAMAMOTO 等[14]开发的珠链模型(Bead-chain model),采用离散元软件 EDEM 将完整纤维离散化成相互连接的颗粒单元来建立柔性纤维模型。珠链模型将纤维离散成一串相互粘结的球体,球体之间的粘合强度由拉伸、弯曲和扭转常数三个参数定义。通过改变上述三个参数的大小,可以改变球体之间的结合强度,使得每对球体都可以拉伸、弯曲和扭转,从而改变纤维的柔韧性。
为了便于模型的分析与求解,本文计算和建模基于以下基本假设:① 柔性纤维悬浮在不可压缩非牛顿流体中;② 流场为简单剪切流场,且不受纤维运动的影响;③ 纤维直径均匀、性能一致且在运动中不发生断裂;④ 忽略纤维的扭转和相互碰撞。
在珠链模型中,单根纤维被离散成 N 个半径为a 的球体,这些球体排列成一束,并与每个相邻的球体粘合在一起,组合成一个长度为 2aN、直径为2a、长宽比为 N 的圆柱形杆。每一对粘合的球体可以通过改变它们的结合距离和结合角度来伸展和弯曲。
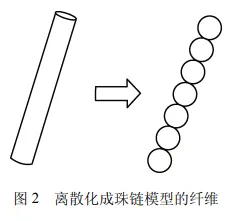
施加在一对相邻的球体 i、j 上的拉伸力 s Fij 取决于两球体中心的距离 r。如果两球体从平衡距离被拉长,拉伸力会施加在每个球体上以恢复相邻两球体之间的平衡距离[14]
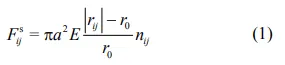
式中,E 是纤维弹性模量;rij 为球体 i 中心指向球体 j 中心的向量,r0 为球体之和球体于中心的初始距离;nij 是从球体 i 中心指向球体 j 中心的单位矢量。

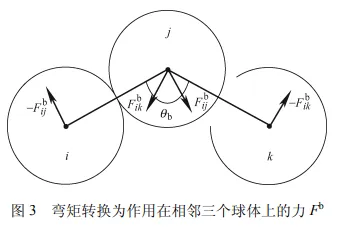
考虑三个依次相连的球体 i、j、k,球体之间联结键的弯曲相互作用是球体之间键角 θb 的函数。如果模型发生弯曲,其球体之间的键角会从它们的平衡角 θb0 发生改变(平衡状态时 θb0=0°),则弯矩 Tb由以下公式给出[15]
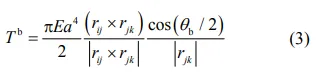
基于式(3)计算出弯矩,则作用在球体 i、j、k上的由弯矩产生的力 Fb 可以由以下公式计算得出[16]
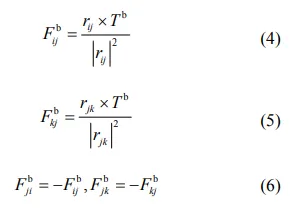
计算该力的过程适用于纤维模型中每一组三个依次相连的球体。
上述方程求得纤维模型中球体所受的力满足以下公式
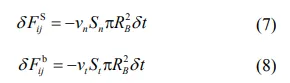
式中,Sn和 St分别为法向和切向刚度;vn和 vt分别为颗粒的法向和切向速度;RB为联结键半径;δt 为时间步长。
通过上述方程可以求得颗粒间联结键的法向和切向刚度。当达到联结键的生成时间时,所有定义的接触颗粒将被连接在一起,建立柔性纤维模型。
2.2 固液两相流模型
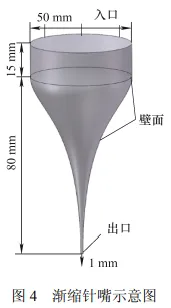
在离散元软件 EDEM 中,使用 Bonding V2 接触模型定义颗粒之间的联结键,使得颗粒在联结键生成之后处于联结状态。通过 SolidWorks 和 ANSA完成几何建模和网格生成。为了减少计算时间,模型计算域仅限于针筒部分区域和渐缩针嘴部分,如图 4 所示。
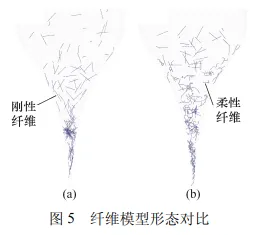
实验所用纤维直径为 6.921 μm,长度为 6 mm,当按照实际尺寸建模时,EDEM 中的颗粒数量远远超出了计算机算力限制。纤维粗粒化模型(Coarse-grained Model)通过把数个小球看作一个小球,可有效简化建模的复杂度,如 LI 等[17]通过粗粒化模型模拟单个血红蛋白纤维,有效观察了血红蛋白的机械行为。因此,本研究用一个直径为 0.1 mm的小球代替 10 个直径为 0.01 mm 的小球,总计 60个直径为 0.1 mm 的小球颗粒串连在一起来模拟单根长度为 6 mm 的碳纤维。如图 5a 所示,当使用刚性纤维模型进行模拟时,纤维无法像真实纤维一样在流场中弯曲变形,并且在运动过程中会因为无法弯曲而在针嘴处发生堵塞。如图 5b 所示,经过柔性化处理后的纤维模型在计算域内运动时,其形态上呈现出不同程度的弯曲变形。表 1 列出了纤维颗粒的物理特性。
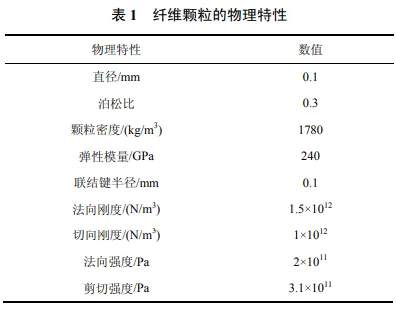
在有限元软件 Fluent 中设置流体相关参数。求解器设置为瞬态求解,流体的流动性质为层流,密度为 1 014 kg/m3,动力黏度为 32 kg/(m·s)。针筒模型上表面设置为压力进口面,进口表压力为0.03 MPa;渐缩针嘴出口设置为压力出口面,出口压力设置为标准大气压。
2.3 EDEM-Fluent 耦合模型的建立
基于 DEM 离散元软件和 CFD 有限元软件的工作原理,两者均不能单独完成固液两相流的模拟分析,但是通过建立 DEM 与 CFD 的耦合框架可以将这两类软件联系起来,使其利用各自的计算优势完成固液两相流的数值模拟。在耦合模拟中,EDEM负责生成颗粒,计算固相运动、动态和碰撞特性;Fluent 模拟液相中的瞬态流场。搭建的耦合框架可实现两个软件之间的数据交互,继而完成耦合模拟。
仿真开始后,在压力作用下,流体在通道内流动,形成渐缩流场。柔性纤维在流场入口面上随机生成,并跟随流体在流场中运动。
3 仿真结果分析
3.1 整体纤维分布
图 6 显示了纤维颗粒在仿真开始后不同时间段在流场中的运动过程,其中颗粒的颜色代表颗粒移动速度。初始时刻,压力作用在流场进口面,并且该面上随机生成纤维。在 t=0.3 s 时,流场入口处已随机生成部分纤维,纤维的轴向在空间内随机朝向。在 t=0.7 s 时,流场中的纤维分布已略微呈现出“倒三角”的形状,管道中间的纤维下落较壁面附近的纤维快。这是因为受壁面影响,近壁处的流体速度最小,管道中心处的流体速度最大,反映了连续流体的抛物线型速度曲线。在 t=1.2 s 时,流体携带纤维颗粒进入渐缩管道,流体域发生收缩,横截面直径减小,导致流体速度进一步增加。在渐缩管道的中心区域,流体在流动方向的速度差变大,导致纤维受到较大的轴向剪切力,继而发生翻转,其轴向方向逐渐趋于流体流动方向。在 t=1.5 s 时刻,大部分纤维颗粒进入渐缩管道,流道直径减小,纤维颗粒沿着流体流动方向分布在渐缩喷嘴中。当流体携带纤维颗粒运动到喷嘴出口处时,纤维颗粒的轴向方向总是沿着挤出方向流出管道。

3.2 单根纤维运动分析
选取下落速度最快的三根纤维查看其速度随时间的变化曲线,如图 7 所示。从图 7 中可以看出,初始时刻,纤维开始生成,速度为 0。随着时间的推移,纤维的速度逐渐加快。在 0.3~1.2 s 时间段内,纤维速度增加较为平缓,而之后的 0.3 s 内,纤维速度发生突变,在这一时间段内,纤维运动至渐缩针管中,管道发生收缩,导致流体速度迅速增加,纤维速度也随之增加。

图 8 是单根纤维在流场中的运动过程图。在初始时刻 0.2 s,该纤维生成,其在流场中的朝向大致沿着水平方向;在 0.2~0.7 s 这一时间段内,纤维在流场中下落的同时,其形态也发生变化,靠近流场轴心位置的颗粒下落速度更快,导致纤维形态发生弯曲;0.7~1.2 s 时间段内,纤维下落距离变大,方向发生了更大的偏转;到 1.5 s时,纤维已趋近于与壁面平行,并且下落距离进一步增大。
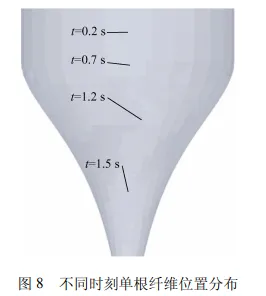
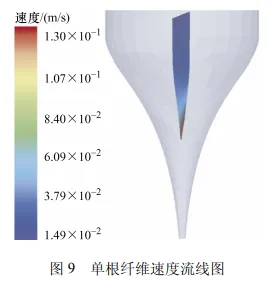
图 9 是单根纤维在 1.5 s 内的速度流线图。通过流线图可以清楚地看到组成纤维的颗粒在流场中的速度分布以及纤维的方向变化。可以看出,纤维在流场中运动时,形态逐渐从水平变化为竖直朝向。由于纤维模型是由多个颗粒组成,纤维在流场内的运动可以分解为众多颗粒的运动。受到流场的影响,各个颗粒的速度不尽相同。组成一根纤维的颗粒之间存在速度差,纤维不同区域下落的速度不同,速度较大的部分下落较快,导致纤维在下落过程中会逐渐沿着流动方向发生偏转。
3.3 流场速度分析
流场在 t=1.5 s 时刻的速度分布如图 10 所示。
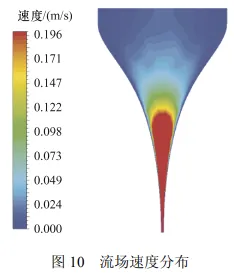
由图可知,管壁附近的流速较小,管轴区域的流速较大,而且越靠近渐缩针嘴部分,流速越大,最终在针嘴出口处速度达到最大。因为层流的流动特性,管壁附近的流体受到壁面的影响,因此越靠近针嘴部分,在相同时间内颗粒下落速度越快,这与图 7所示颗粒的速度趋势吻合。
3.4 纤维取向排布
为了进一步探究纤维取向度的变化,对纤维悬浮液从渐缩流场流出时纤维在滤网上的取向行为进行仿真模拟。为了模拟实验中用来铺层纤维悬浮液的滤网,在仿真模型中渐缩针筒的下方放置一块沿直线运动的平板,如图 11 所示。平板的运动速度为实验中三轴移动平台中 x 轴的速度,渐缩针嘴距离平板的高度为实验中针嘴距离滤网的垂直距离。平板沿着 x 轴方向运动时,纤维跟随流体从针嘴落下,并铺层在平板上。

从仿真结果可以看出,随着平板的运动,纤维从渐缩针嘴流出后沿着平板运动的方向均匀排列在平板上,有良好的取向效果。模拟结果表明,柔性纤维在渐缩流场中运动时,在剪切力作用下会发生偏转,使得纤维在流场中沿着流体流动方向获得定向排布。当悬浮液流出流场时,纤维会沿着移动方向在平板上完成取向。
4 实验
4.1 纤维毡取向度的表征
为了验证仿真模型的合理性,制备了取向碳纤维,参照李森等人[18]关于纤维取向度的计算方法对纤维毡的取向度进行表征。纤维毡中纤维的取向状态通常使用概率分布函数的矩阵(方向张量)来描述[19]。该张量的分量可用来绘制纤维的取向椭圆,其中椭圆的长轴方向表示纤维整体取向,长轴大小表示纤维整体取向程度。椭圆越狭长表示纤维整体的取向程度越高 [20] ;纤维取向度 (Preferentialalignment degree, PAD)反应了纤维取向的优劣程度,PAD 越小,纤维取向程度越差;反之纤维取向程度越好[21]。
采用湿法取向技术制备短切碳纤维取向毡,并和未取向纤维毡进行对比。其中,未取向纤维毡的制备方法如下:将制备完成的纤维悬浮液倾倒在滤网上,用薄板将纤维液涂抹均匀,抽滤掉其中的分散剂和水分后得到未取向纤维毡。分别剪取制备的未取向纤维毡和取向纤维毡试样,观察其取向效果。6 mm 短切碳纤维毡在不同工艺条件下的微观图、二阶方向张量及取向椭圆如图 12 所示。其中,a 组是未使用取向工艺制备的短切碳纤维无纺毡;b 组是采用湿法取向技术制备的短切碳纤维取向毡。a 组中纤维的排列十分混乱,取向度仅有 57%;而 b 组中短切碳纤维在经过取向后方向明显改变,纤维丝束均沿着渐缩喷嘴移动方向排布,取向度可达 98%,取向效果显著。

4.2 纤维取向对复合材料弯曲性能影响
为了研究纤维取向度对其制备的复合材料性能的影响,采用模压成型工艺制备 CF/EP 复合材料。使用岛津仪器(苏州)有限公司的电子万能材料试验机 AGX-V100KN,按照 GB/T 1449—2005[22]测试CF/EP 复合材料的弯曲性能(样条尺寸 40 mm×15mm×2mm),将上述工艺制备的取向纤维毡和非取向纤维毡裁剪成形状和尺寸一致的预成型坯料并层叠放在模具中。环氧树脂和固化剂按照质量比 4:1的比例调配,搅拌均匀后注入模具中充分浸渍纤维毡,随后加压至 5 MPa,在 120 ℃下保温 3 h 后冷却至室温,从模具中取出试样,将表面打磨平整,得到 CF/EP 复合材料。
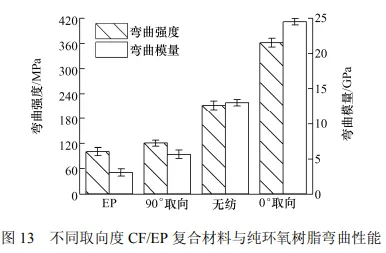
不同取向度的 6 mm 碳纤维复合材料与纯环氧树脂弯曲性能如图 13 所示。由图 13 可知,6mm0°取向毡复合材料相对于未取向毡的弯曲强度和模量分别提升了 70.6%和 88.5%;而相对于90°取向毡性能提升了 200%和 337.5%。这是因为纤维毡中的纤维按照 0°方向排列时,碳纤维轴向优异的力学特性能得到充分发挥,因此复合材料在纤维轴向的力学性能大幅度提升。上述结果表明,CF/EP 复合材料的力学性能与纤维的取向度有关,纤维毡中纤维的取向度越高,其制备的复合材料力学性能越强。
4.3 结果讨论
试验表明,纤维悬浮液在空气压力作用下从针筒形渐缩流场中挤出,并利用壁面收缩产生的剪切力使纤维在流体中完成取向。三轴移动平台可对喷嘴的移动路径进行自由编辑,使得制备的取向纤维毡不仅仅局限于单向取向,从而提供更多个性化的取向方向选择,以满足不同性能对取向方向的需求。
5 结论
1) 基于珠链模型和柔性纤维动力学方程,通过 EDEM 中的元颗粒功能与 Bonding V2 模型对纤维进行柔性化处理,使得纤维在运动过程中可发生不同程度的弯曲变形;搭建了 EDEM-Fluent 耦合数值模型,对纤维-流体的固液两相流进行了数值模拟,分析了纤维在渐缩流场中的运动规律。
2) 仿真结果表明:柔性纤维在渐缩流场中的流动是以壁面为主导的剪切排列过程。在流场入口处,纤维呈现随机分布状态,在气压作用下悬浮液携带着纤维颗粒在渐缩流场中向下运动。柔性纤维在渐缩流场中的速度受流体的影响。流体的速度特性导致组成纤维的离散元颗粒在流场中受到轴向剪切力的作用,从而导致其速度各不相同,因此组成单根纤维的不同颗粒之间产生速度差,在下落过程中会发生不同程度的弯曲变形和翻转,翻转方向与流动方向相同。
3) 实验结果表明:通过湿法取向平台能够实现对碳纤维的高取向度排布,且可实现路径的自由编辑。当纤维从渐缩针嘴中流出时,其沿着针嘴移动方向在平板上进行铺层,完成纤维的取向排列;制备的取向毡中纤维取向度可达 98%。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删