Vuel学习心得：连接壳单元的cohesive单元应用

因为课题原因，需要用到cohesive单元连接两壳单元的边界，然而ABAQUS中的cohesive单元只有用于连接实体（solid）或者平面单元（平面应力或平面应变）的coh单元，在导师的催促下就只能从零开始自学自定义单元的内容，最后也终于基本实现这个目标。自学的过程很辛苦，其中很多东西考虑的也并不是很充分，理解的也不一定到位，但结果实现了目标，还是很开心的。

当然这个过程中很感谢snowwave02和借风一尺两位的帮助，学术方面大家多交流才会进步。

话不多说，进入正题。其实这种单元在DYNA中是有的，但是因为课题原因希望进行对coh单元本构更多的二次开发，且DYNA的二次开发我不是很熟悉，因此我就直接把DYNA的理论搬过来用了。但是鉴于二者还是有所不同，因此我在一些细节部分进行了个人的修改。这次的介绍主要理论源自于一篇DYNA会议上的文章：Edge-to-edge Cohesive Shell Elements in LS-DYNA, 作者是Jesper Karlsson, 如果有兴趣可以找原文查看。

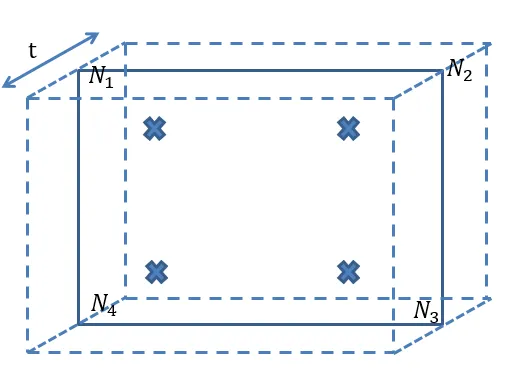
单元的基本形式如上图所示，四个节点，N1,N2用于和上边的壳单元（ABAQUS关键字S4）相连，N3，N4则和下边的壳连接。壳的厚度为t，采用常规的四个积分点（图中画“×”的位置），积分点的等参坐标也是非常常见的：  (±1/√3,±1/√3)。对于每个节点均开放六个自由度，即三个平动三个转动。

接下来是运动学的定义：

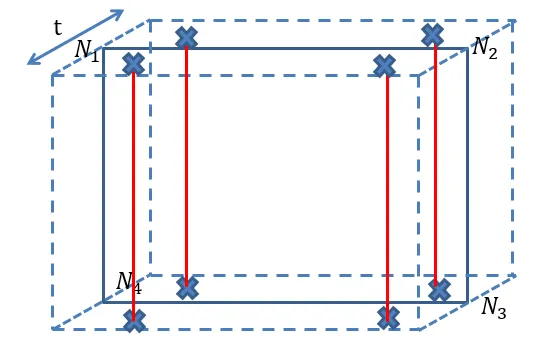
d代表分离量，即traction-separation法则中的分离距离，xt和xb分别代表上下边在对应等参坐标下的坐标位置，xi（i=1，2，3，4）代表节点的坐标，η 和   ξ 是等参坐标。按照这种方式算出来在积分点的分离量d如下图红线所示意，因为有四个积分点，恰好有四段d，这也是很清晰的。R则是旋转矩阵，因为traction-separation需要在局部坐标系下讨论，因此需要旋转矩阵沟通局部与全局坐标系。ni（i=1，2，3，4）代表对应节点处的法向方向。

本构关系方面，就比较简单：

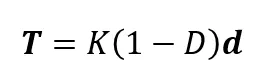
其中d是刚刚定义的分离量，T则是cohesive法则中的牵引力，K是刚度，D是损伤系数，因此只需要完成D的更新，就可以实现本构。不同的traction-separation法则D的更新有所不同，这篇帖子主要不是讲本构的更新，因此这一部分就略过。

VUEL中需要用户代码定义三个内容：质量矩阵、节点内力以及临界稳定步长，首先讨论节点力。

定义节点力一般需要从虚功率方程出发，首先我们写出虚功率方程：

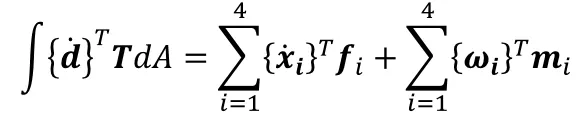
上式中，d是之前介绍的分离量，T为牵引力，f是节点内力，m是节点内转矩，x是节点坐标，omiga是角速度。

另一方面，上面虚功率方程的左端可以展开，直接带入帖子最前面运动学的定义：

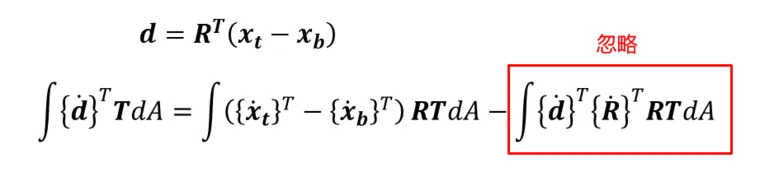
上式中忽略最后一项，因为认为旋转矩阵的变化是很小的，将xt和xb分别对时间求导（二者的表达式上文已经给出）再带入，对比虚功率方程右端以及刚刚展开式子的右端，就可以得到节点内力以及节点弯矩的表达式：

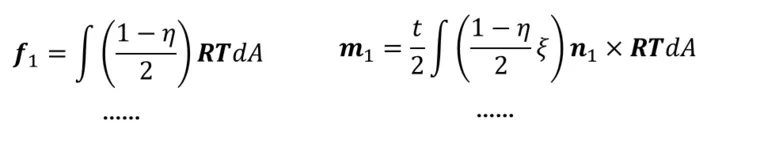
（表达式太多就不打全了，可以自行推导）

当然，要找到上面积分的原函数是很困难的，帖子最开始说的数值积分就是需要用在这个时候的！由高斯积分法，函数在某个区域的积分可以看作在区域内某几个点对应函数值的求和，写成表达式的话有：

其中

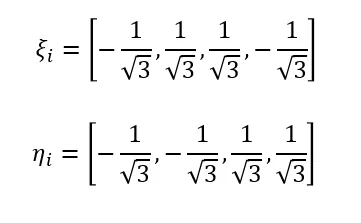
有了数值积分的工具，我们就可以把上面求得的积分式算出来，我把他们全部列出来：

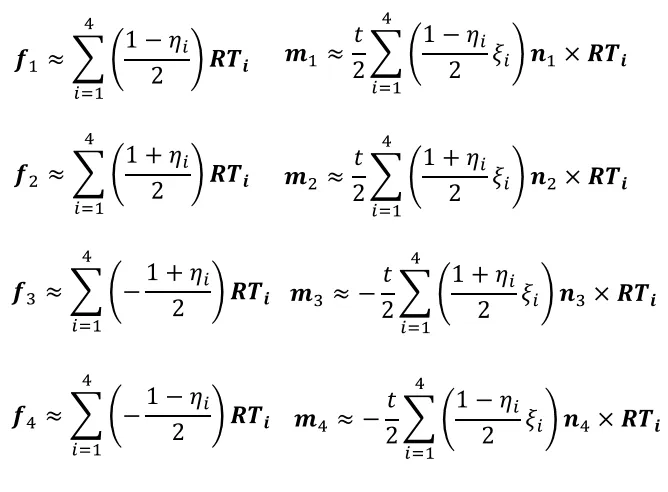
观察上面的这些式子，我们看一下哪些值我们还没有。首先，T是通过本构关系求得的，已经更新完毕；积分点的等参坐标都是给定的；t是参数，也是知道的；所以我们没有的量是旋转矩阵R和法向量n。

首先讲讲节点的法向量n，在下图中用红色箭头示意，这里面n默认是单位向量。

ABAQUS在更新是都会给出每个节点的转角增量，那么我们从这个转角增量，根据罗德里格旋转公式，就可以得到新的法向量：

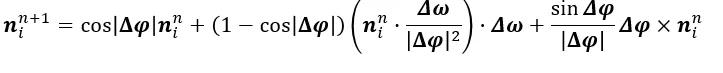
这样我们每一步都会更新一个n，然后我们把他存到历史变量中，它就会随着有限元计算一步一步更新了

好了，下面介绍旋转矩阵R的更新：

这样我们就有了R：

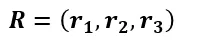
同样把R存到状态变量中，一步步更新

至此我们就有了f和m中所有需要的量，也就可以完成节点内力（弯矩）的所有更新

然后是质量矩阵，我的质量矩阵就比较随意，采用的是集中质量矩阵，意思是只有对角线上有非零值，由于质量守恒，因此质量矩阵应该是个常量，所以我就在对角线上随意给了一个量（意思是对角线上都是这同一个值，其他地方都是0），没想到最后也能跑通，关于质量矩阵怎么给，也想和大家更多交流。

最后是临界时间步长，我也是参考有限元书上的公式自己定义了一个量：

其中beta是系数，按照书中内容我取了0.95，E和rho分别代表模量和密度。

以上就将所有量更新完毕，这个单元就可以用了。

展示一下效果：

两个大的单元都是纯弹性的壳单元（S4），打“×”的地方就是刚刚写的VUEL，还是实现了预期的功能了的

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删