ABAQUS知识解析剪切闭锁现象及其影响

完全积分的一阶单元在每个方向上使用2个积分点。因此，三维单元C3D8在单元中存在2 × 2 × 2的积分点数组。完全积分的二阶单元每个方向上有3个积分点，如下图：

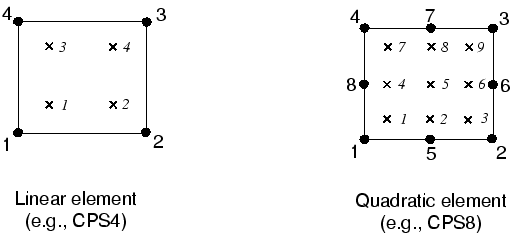
探究元素的阶数(一阶与二阶)和网格密度对结果精度的影响

采用了几种不同单元和网格密度,在Abaqus/Standard模拟悬臂梁问题：

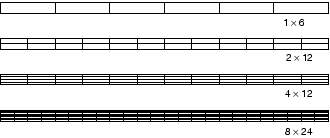
各个模拟的末端挠度位移与理论值3.09 mm的比值如下：

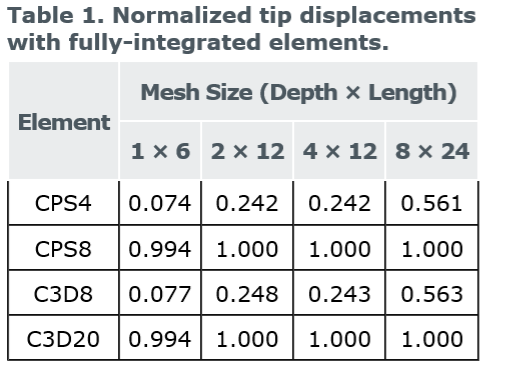
对于线性的，完全集成的单元，单元再密都不准。以上挠度模拟不准是因为剪切锁紧引起的，这是所有完全积分的一阶实体单元都存在的问题==

什么是剪切闭锁？（shear lock）

剪切锁紧会导致单元在弯曲时过于僵硬。

根据材料力学，一个材料微元承受弯矩M时的变形如下：

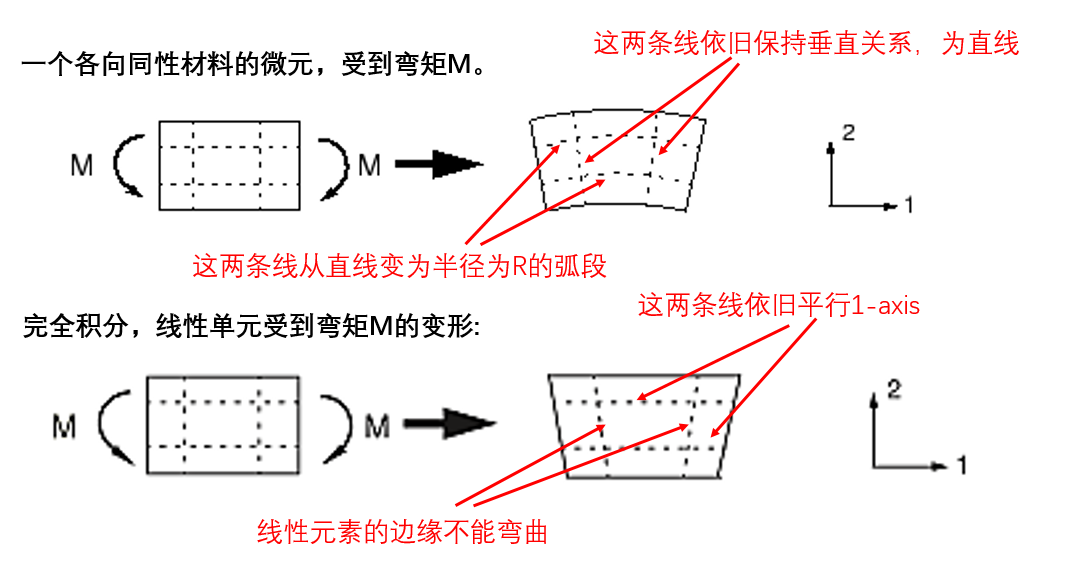
单元变形的应力情况：

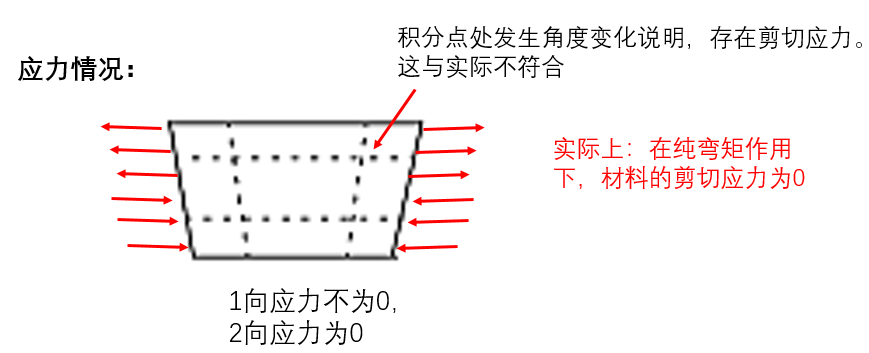
这

种不正确的剪切应力的产生是因为线性单元的边无法弯曲。剪切应力的存在意味着单元应变导致剪切变形，而不是预期的弯曲变形，因此整体挠度较小，也就是说单元刚度太大了

剪切锁定只影响完全积分的一阶单元在弯曲载荷下的单元性能。

对于二阶单元，剪切闭锁不是问题，因为二阶单元的边是可以弯曲的，但它依旧有细微的剪切闭锁效应。

所以，ABAQUS文档建议：
   

只有相当确定载荷会在模型中产生很小的弯曲时，才推荐使用完全积分的一阶单元。完全积分的二阶单元在复杂的应力状态也可能shear lock。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删