1 概述
本系列文章研究成熟的有限元理论基础及在商用有限元软件的实现方式,通过
1) 基础理论
2) 商软操作
3) 自编程序
三者结合的方式将复杂繁琐的结构有限元理论通过简单直观的方式展现出来,同时深层次的学习有限元理论和商业软件的内部实现原理。
有限元的理论发展了几十年已经相当成熟,商用有限元软件同样也是采用这些成熟的有限元理论,只是在实际应用过程中,商用CAE软件在传统的理论基础上会做相应的修正以解决工程中遇到的不同问题,且各家软件的修正方法都不一样,每个主流商用软件手册中都会注明各个单元的理论采用了哪种理论公式,但都只是提一下用什么方法修正,很多没有具体的实现公式。商用软件对外就是一个黑盒子,除了开发人员,使用人员只能在黑盒子外猜测内部实现方式。
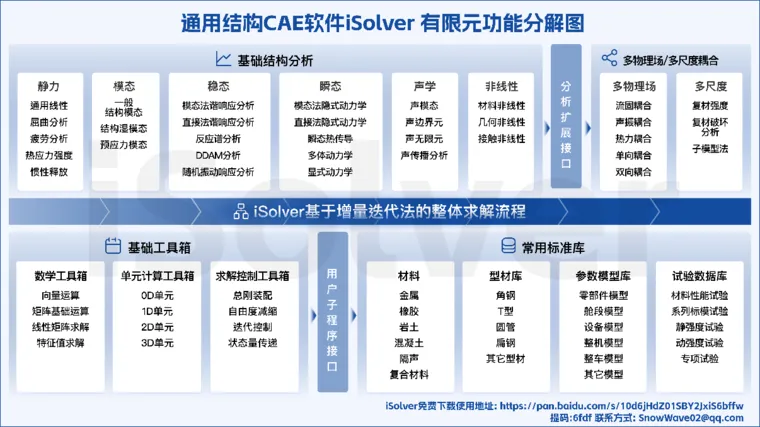
一方面我们查阅各个主流商用软件的理论手册并通过进行大量的资料查阅猜测内部修正方法,另一方面我们自己编程实现结构有限元软件iSolver,通过自研CAE软件和商软的结果比较来验证我们的猜测,如同管中窥豹一般来研究的修正方法,从而猜测商用有限元软件的内部计算方法。我们关注CAE中的结构有限元,所以主要选择了商用结构有限元软件中文档相对较完备的Abaqus来研究内部实现方式,同时对某些问题也会涉及其它的Nastran/Ansys等商软。为了理解方便有很多问题在数学上其实并不严谨,同时由于水平有限可能有许多的理论错误,欢迎交流讨论,也期待有更多的合作机会。iSolver包括完整的前后处理和有限元求解器,功能如下,有兴趣可直接在下面网址下载:
百度网盘链接: https://pan.baidu.com/s/10d6jHdZ01SBY2JxiS6bffw 提取码: 6fdf
2 声学分析
Abaqus虽然是结构计算软件,但如今随着系统的复杂,结构与其它物理场的耦合也越来越频繁,因此,Abaqus也将自己的计算能力往其它物理场扩展,其中,热学、声学、流体和电磁学等都是Abaqus多物理场的扩展的典型应用。
热学主要计算热膨胀时结构应力的变化和热传导等现象,本身和结构关系密切,所以Nastran、Abaqus等结构软件都会包括热分析功能;流体由于达索已经收购了业界两款最好的基于最近大热的LBM粒子算法的商业软件PowerFlow和Xflow,可能处于产品线的发展考虑,把基于有限元方法的Abaqus/CFD模块直接停止开发了,但保留了Abaqus中的CEL模块,专门处理流固耦合问题;而声学模块主要处理声腔内的模态分析和声传播问题;
电磁模块至今不涉及,在此不讨论了。这几个多物理场的扩展每一项都需要单独的其它物理场的专业知识和结构专业的融合,也许大家都和我们一样只熟悉结构的算法,对陌生的其它专业总觉得非常难,但其实静下心来系统学习一下,其它专业的内容并不是想象的那么困难,结构有限元学好了,其它专业都是一通百通的。
譬如下面的声学有限元理论公式我们就可以完全按照结构有限元的流程推导。我们在实际研发CAE软件过程中发现难的不是这些多物理场公式等的编写,难的是如何在现有的结构CAE软件基础上在前后处理和求解器层面分别加入其它分析能力,同时又保持原有框架的可扩展性和易维护性,当然,抛开多物理场,就算仅研发结构CAE软件如何在维持现有框架结构基础上在软件层面添加新的功能也是实际中我们需要花大力气研究的一个关键点,这也是我们理解的在研发上理论上的有限元和工程上的有限元分析的最大区别。

现阶段我们只讨论声学物理场,由于声学涉及的问题较多,我们仅限于和实际工作中用到的和结构强相关的部分内容,水平有限,同时对声学理论等理解的也不够透彻,可能有很多问题,大家有疑问也欢迎多讨论。
2.1.1 湿模态概念
一个结构体在真空中的振动和在周围流体介质中的振动有时差异巨大,必须分开考虑,此时有干湿模态之分,以下干湿模态概念选之:结构振动问题中的干模态和湿模态 - 知乎 (zhihu.com)
模态分析是结构动力学问题中最为普遍的一个问题,大家对这个概念也非常熟悉,它是结构的固有特性,在不考虑阻尼的影响下,只与结构的刚度和质量有直接关系。
本文所涉及的问题是有关干、湿模态的计算,属于模态问题中经常遇到的问题。通常我们所计算的模态其实是干模态,主要是由于结构放置在空气中而空气这一流体对结构的影响几乎可以忽略不计,所以基本上可以默认为就是干模态。
但是严格意义上讲,受流体附带阻尼及刚度的影响,这类的模态仍然是湿模态。所谓湿模态是考虑流体对结构的作用,也就是在通用的振动方程中加入了有关流体的附加质量及刚度矩阵(Kx、Mx),这块相互作用对结构的模态存在一定的影响,尤其是涉及诸如油、水等液体的作用。举例来讲,司马光砸缸的那口缸,在加水和不加水的情况下,砸缸的声音肯定是不一样的,一个明显清脆宽广,一个就显得沉闷。再比如我们车载的油箱结构,在加满汽油和未加满汽油的情况下,两者的模态肯定是不一样的。另外还有诸如潜艇、船舶、油罐车等结构。所以,对于受到液体作用显著的结构,我们在计算的时候需要研究其湿模态。
2.1.2 湿模态分析方法
当结构体内部或者外部和流体接触时,结构受到流体的压力作用而发生变形,而变形又会反过来对流体边界有影响,形成一个流体压力->结构变形->流体压力变化的典型流固耦合系统。流固耦合的体系相当庞大,我们只讨论流体载荷对一个振动结构的耦合作用。

有两种可能的情况:
1)一种可能是结构变形导致流体压缩或膨胀,影响流体对结构的压力,典型例子是船体或者浮动平台越来越长后,会影响船体周围的波浪形式。

一般认为当无量纲
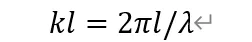
不是一个小量时,会出现这个情况。其中l是结构体的特征长度,是流体中载荷的波长,也就是结构体的特征长度和流体中载荷的波长可比拟。个人理解工程上可以采用两种方式求解:
a. 流体用边界元形式,但边界考虑了流固耦合,属于气弹性(aero-elasticity)和水弹性(hydro-elasticity)的范畴,一直觉得照原理来说应该比下面的虚拟质量法来算湿模态更准,和做水弹性的专家聊过,实际上水弹性都还是基于干结构的模态基展开来计算结构动响应,所以输入的是干结构的模态分析后处理文件,程序内部应该没有计算湿模态,水弹性和气弹性还是只计算流体载荷,不是算结构振动的。
b. 流体用声学有限元形式,然后用Nastran的glue或者Abaqus的Tie和结构有限元绑定,此时流体的压力会作为外载荷作用到结构上,耦合面结构的加速度也会作为声学有限元的边界,即前面声学有限元章节中的Inward volume acceleration。这种方法从原理上来说也比下面的虚拟质量方法更加正确,但建模相对复杂,譬如如果是水域的话,见过外面的流体域大概取到结构体的6倍以上共振频率解才能稳定,这样导致网格量大大上升,所以在工程上反而不够实用。
2)另一种结构的变形不会导致流体载荷的变化,譬如海浪中一块小木板的变形不会对波浪载荷有影响,即单向耦合。也就是当kl<<1,此时结构体相对于流体载荷中的波长可忽略。
此时流体假定不可压、无粘,可以用势流理论的边界元表示流体,然后流体的作用等效为虚拟质量加到结构质量上,而流体对结构的刚度阵的影响忽略,至于和上面的气弹性或者水弹性的边界元+结构有限元的方法的不同,有可能仅在耦合边界的处理上,这边只有单向的流体对结构的压力传递,而上面的是双向的,仅猜测,不一定对。
这种方法虽然理论上不如上面的流固双向耦合精确,但流体只要建一层边界就行,所以工程上相对更实用。在结构商软中,Nastran的MFluid和ACMODL分别模拟虚拟质量法和流固耦合模态分析,其中MFluid虚质量分析功能是由戴姆勒.奔驰公司提供资金支持开发的一个功能模块,目的是计算油箱等流固耦合部件在高频响应。而Ansys、Abaqus暂时没有虚拟质量方法,都是直接采用基于声学有限元的流固耦合来求湿模态。
本章只介绍基于虚拟质量的湿模态计算。
2.2 基于虚拟质量的湿模态计算理论
无粘状态下,不考虑剪切应力,所以只有一个正压力未知量,流体正压力中包括两部分:
一部分是静压,不随时间变化,静压对结构会产生一个初始应力和位移,结构强度足够的话,这种小变形导致的振动影响非常小
另一部分是动压,只有动压才会对振动有大的影响,无粘状态下这种在稳定的流体场基础上叠加的动压就是声压。既然是声压,那么就可以用前面统一的Helmholtz方程:
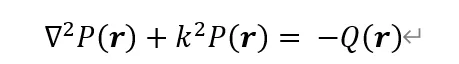
在结构振动过程中,流体域中我们假定没有声源,这样依然能直接使用上一章的边界元理论得到的近似方程。
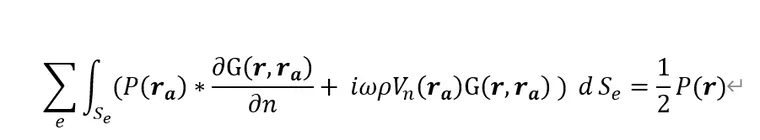

上式是声压和速度的关系,需要转换为力和加速度的关系。做以下变换
• Pi是流体对边界元的压力,朝结构内部法向,但速度边界还是超流体法向,所以需要将Pi变号,使得力和速度方向一致。
• 压强需要转换到节点力,转换方式和结构有限元的面载荷转到集中力载荷一致,设为:
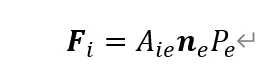
• 速度转换为加速度,此时需要考虑方向
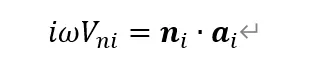
最终得到:

2)因为P可以由直接获得,所以P和Vn都是同类型单元更合理,但如果都采用线性单元,那么B的计算量相对要多很多,因此还是都是常单元效率更高些,此时:

其实和上面单元相比只是C的形函数从积分内移动到了积分外,没有本质的区别,结果也非常相近,无论哪种都不足以解释后面我们将谈到的和Nastran的精度误差。
最后来说说Green函数G。因为一般来说声音是可压缩的,G是复数,M正常来说也会是一个复数形式,这样就会得到复数形式的模态,但前面说过,在这儿,因为假设不可压,那么相当于声速无穷大,也就是k->0,这也和k*l<<1的假设是一致的。
则

也就是G最终简化为实数,使得M也是实数,相当于原始Helmholtz方程简化为了Laplace方程:
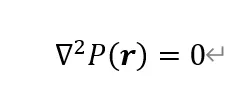
2.3 基于iSolver流程的湿模态的工程实现
对标Nastran的MFluid功能,基于iSolver的湿模态工程实现上还做了以下几个关键步骤:
(1)自由面处理:Nastran的MFluid可以处理包括流体自由面(Free Surface)的情况,这也是非常常见的一个情况,一个典型问题是譬如单面法向向上的平板,自由面在板的上方,当自由面越来越接近平板时,理论上应该会得到真空中模态结果。在iSolver中,我们采用了镜像湿面元的形式求解流体自由面的情况,同时在iSolver界面中可设置有无自由面及自由面高度。
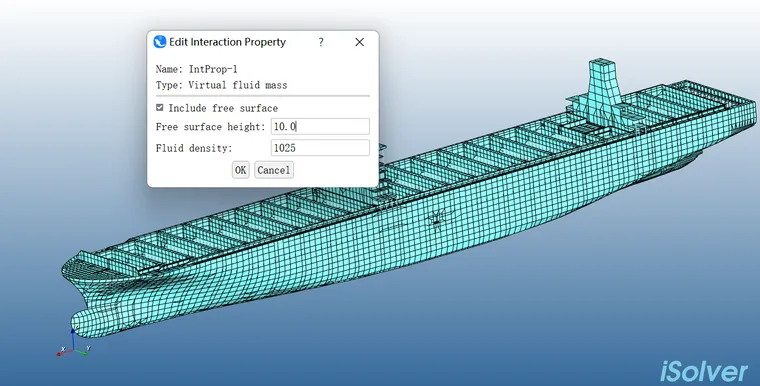
(2)界面流程:Nastran的MFluid没有界面,只能在bdf关键词中添加,譬如,
MFLUID,2,0,10.0,1025.0,3,,N,N
ELIST,3,110001,THRU,116000
表示海水密度是1025,10m高的自由面,对110001到116000号单元中位于自由面下方的单元施加虚拟流体质量。MFLUID的关键词很容易编辑,但ELIST单元号对不连续的湿表面单元手工很难列举。在算法层面自主软件很难超越商软,只能在这些前后处理的个别小点上做些更加人性化的设置,在iSolver中可以直接在三维图形上选取施加湿面元的单元,同时,不要求湿单元连续编号,后续我们还将把iSolver前处理产生的虚拟质量关键词和湿单元信息自动输出到bdf文件中,为那些想调用Nastran来求湿模态的用户解决点Patran无法实现的功能。
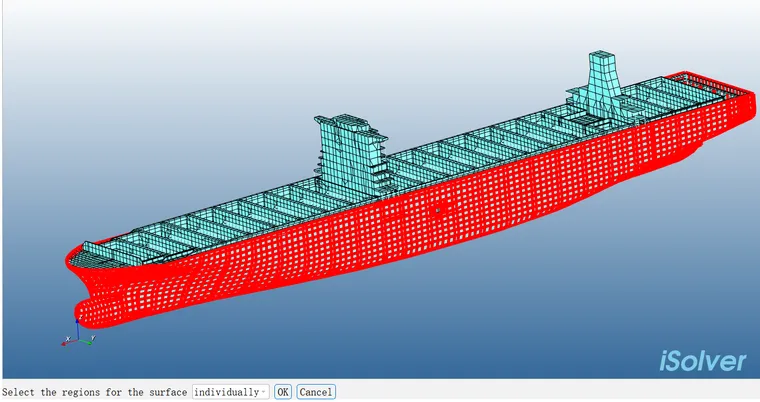
(3)精度的考核:iSolver实现后,我们发现和Nastran的MFluid的部分结果存在部分差异,基频普遍略大,而高阶频率差异较小,具体如下面示例展示,研究了很久,对上面我们贴的算法做了大量的调整,依然得不到和Nastran的MFluid差异非常小的湿模态结果,我们把和Nastran的对比结果贴在下方,还需做过这方面工作的高手指点。
2.4 矩形板湿模态模型验证
2.4.1 算例介绍
单位采用SI制,模型为一个10X5大小的矩形板,厚度t=0.1,材料杨氏模量2.01e11,泊松比=0.31,密度7920。四周铰支。

2.4.2 iSolver虚拟质量结果
iSolver中将矩形板划分为0.5大小网格,单面加无限深水时,iSolver基频结果:

• *网格大小影响不是很大,如果划分成0.25,频率基本不变
前10阶如下
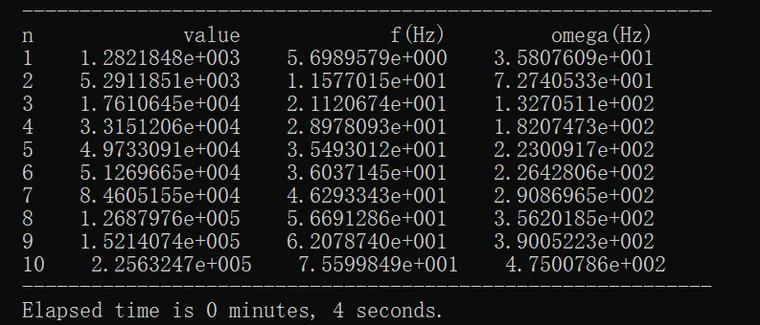
2.4.3 Nastran虚拟质量结果
在iSolver中将模型一键输出bdf到Nastran,由于Nastran的MFluid关键词中没找到不设置自由面的方法,所以直接设了一个108的深度,对10X5米的板来说自由面影响基本可忽略,得到基频6.57Hz:
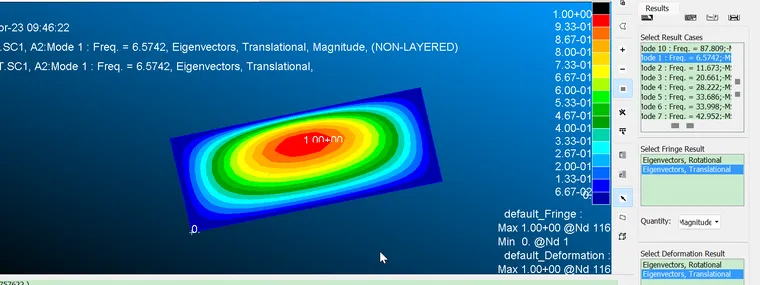
2.4.4 Abaqus结构+声学有限元湿模态结果
Abaqus用声学有限单元模拟流体结果,水密度设置为1025,用Tie将板结构和声学单元绑定,为排除水域尺寸的影响,参考相关文件,取12倍结构尺寸的水域,Abaqus中分析后三阶频率分别为5.9085,11.605,21.349
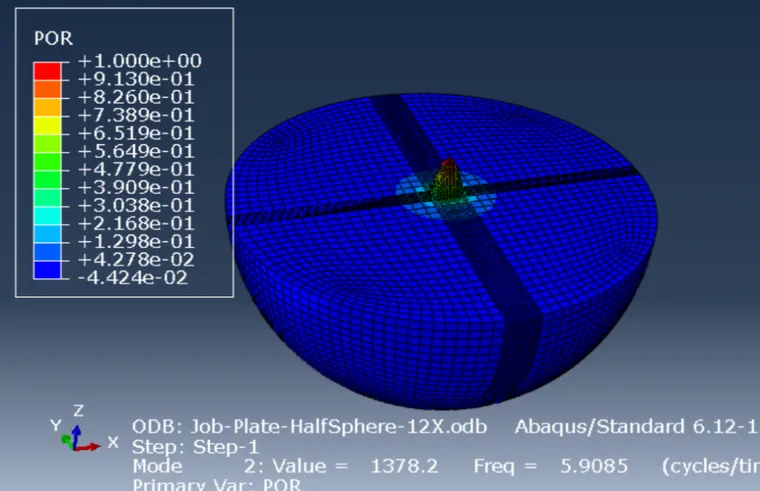
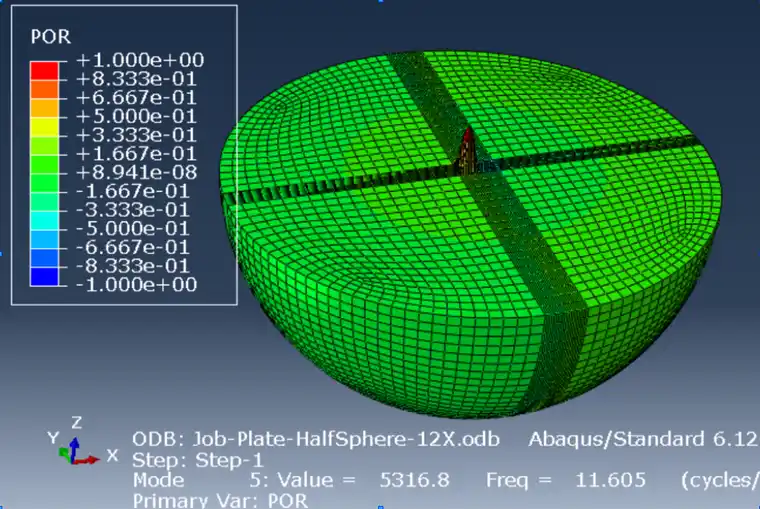

2.4.5 SAM、Nastran和Abaqus单侧加水湿模态比较
将上述三个软件得到的湿模态的结果汇总到一个表中,可发现iSolver和Nastran的MFluid相比基频较小,但和Abaqus基于结构和声学有限元的基频更接近。2、3阶频率基本一致。我们一直没找到单面加水的矩形板的模态理论值或者试验值,虽然我们的基频结果更接近Abaqus,但实际使用模态分析的时候,用户更关心的是和Nastran的对标,只可惜一致没找到Nastran的MFluid的后台真实的理论修正方法,如果你恰好也做过基于虚拟质量的湿模态,可以尝试一下这个算例结果,或者下载我们的软件对比一下,看看是不是也是这种情况,有问题我们可以一起校核。
| 阶次 | 理论公式(Hz) | iSolver(Hz) | Nastran MFluid(Hz) | Abaqus 结构声学FEM | |
| 干模态 | 1 | 12.01 | 12.10 | 11.91 | |
| 2 | 19.22 | 19.35 | 18.87 | ||
| 3 | 31.23 | 31.75 | 30.51 | ||
| 湿模态(单面接触水) | 1 | 5.70 | 6.57 | 5.90 | |
| 2 | 11.57 | 11.67 | 11.60 | ||
| 3 | 21.12 | 20.66 | 21.34 |
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删