本系列文章研究成熟的有限元理论基础及在商用有限元软件的实现方式,通过
1)基础理论
2)商软操作
3)自编程序
三者结合的方式将复杂繁琐的结构有限元理论通过简单直观的方式展现出来,同时深层次的学习有限元理论和商业软件的内部实现原理。
有限元的理论发展了几十年已经相当成熟,商用有限元软件同样也是采用这些成熟的有限元理论,只是在实际应用过程中,商用CAE软件在传统的理论基础上会做相应的修正以解决工程中遇到的不同问题,且各家软件的修正方法都不一样,每个主流商用软件手册中都会注明各个单元的理论采用了哪种理论公式,但都只是提一下用什么方法修正,很多没有具体的实现公式。商用软件对外就是一个黑盒子,除了开发人员,使用人员只能在黑盒子外猜测内部实现方式。


一方面我们查阅各个主流商用软件的理论手册并通过进行大量的资料查阅猜测内部修正方法,另一方面我们自己编程实现结构有限元求解器,通过自研求解器和商软的结果比较来验证我们的猜测,如同管中窥豹一般来研究的修正方法,从而猜测商用有限元软件的内部计算方法。我们关注CAE中的结构有限元,所以主要选择了商用结构有限元软件中文档相对较完备的Abaqus来研究内部实现方式,同时对某些问题也会涉及其它的Nastran/Ansys等商软。为了理解方便有很多问题在数学上其实并不严谨,同时由于水平有限可能有许多的理论错误,欢迎交流讨论,也期待有更多的合作机会。
通用结构有限元软件iSolver介绍视频:

http://www.jishulink.com/college/video/c12884
虽然现在Abaqus的功能很多,但在上世纪80年代左右Ansys和Nastran如日中天的时候,Abaqus还能杀出一条血路,主要靠的就是它的非线性功能,如果说线性问题Ansys和Nastran是标准,那么非线性问题Abaqus就是标准。
结构非线性主要分为三类:
其实边界非线性的求解的基本算法并不难,难的是碰撞前后的整个方程的变化特别大,不但是接触力发生突变,而且接触点的节点数目等也发生突变,在数值分析中最怕的就是一些参数的突然增加或者消失了,也就是说你的方程的形式不是唯一的,还需要加入一些额外的逻辑判断,同时,边界非线性往往都是和几何大变形大转动耦合在一起的,这些困难都造成边界非线性极易无法收敛的问题。
从做一个自主的带三维交互的CAE软件的角度上来说,前面说的困难还不是最难的,更难的是前处理对几何体的拓扑的表达组织和在整个接触过程中不同时刻点的的两个离散网格边界情况的精确设置和判断,譬如像Abaqus和Ansys一样在一个整车的几万个零部件模型中自动寻找接触对,这些都需要精度较高的CAD内核才能做到,好的商用CAE都是采用商用的Parasolid、Acis库来处理的,但对一般的自主CAE开发者来说价格是难以承受的,这些都严重制约了自主CAE向边界非线性方向发展。
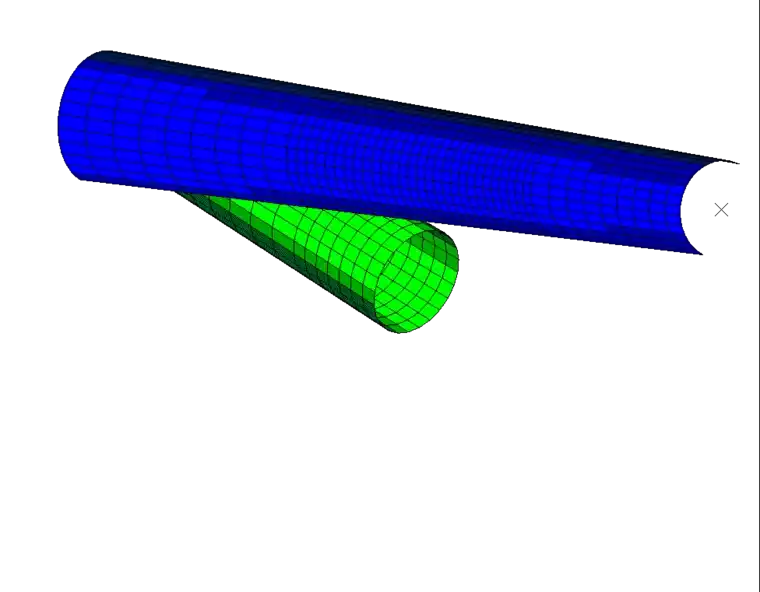
本文我们不讨论前处理的边界非线性的处理,仅讨论后台求解器需要做的接触求解算法,重点还是在如何将接触后的约束关系加入到有限元基本方程中,为后面实现带接触问题的有限元求解打下基础。
有接触不一定就是边界非线性,譬如两个物体用Tie连接在一起,材料依然是线弹性的,应变也没超过5%,那么我们可以认为依然是线性问题,也就不存在边界非线性了。我们认为边界非线性只是接触的一种,边界非线性属于接触的一种特殊情况,我们讨论的接触求解算法同样适用于其它接触问题。



Abaqus Standard的接触求解的整体流程如下,外层按增量法执行,内层按迭代法执行,其实依然是牛顿迭代的范畴,只不过第二步:Form and solve system of equations与只有几何非线性的方程不同,此时需要加入接触的方程的形成和求解。

无论是否存在接触,有限元方程的建立都是实际问题的等效。
1)在没有接触力时
如下图情况,物体在体外力和面外力作用下变化。


有限元方程按照虚功原理求解,在物理上可解释能量守恒原理,即在某一个时刻点,假定在外力作用下有个虚拟的位移,那么外力在虚拟位移下做的虚功=内部应变能的变化相同。

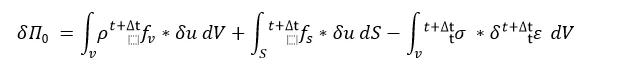
2)当存在接触时
当存在接触时,体积域V和表面积的域包括多个空间独立的物体。譬如下图,两个体的外表面S1,S2发生接触。



接触分法向压力和切向摩擦力,在Abaqus中,如果是法向接触力,在设置Constraint enforce method时就是选择接触算法
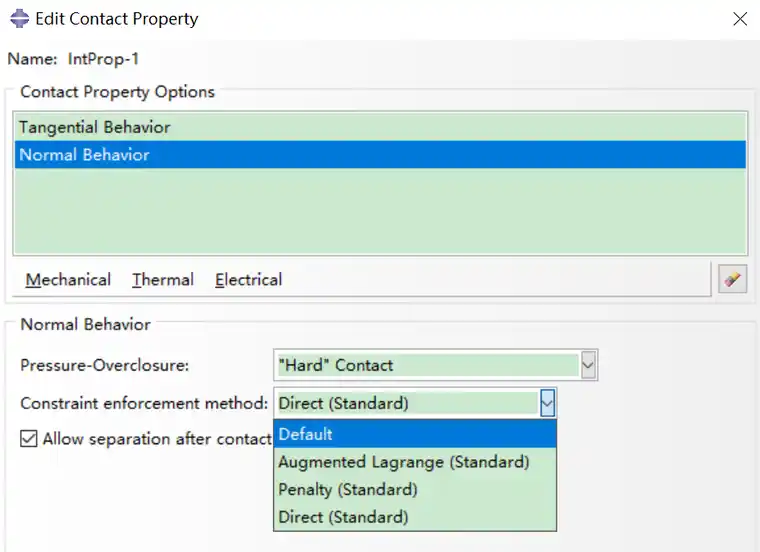

可以选择Direct、Penalty、Augmented Lagrange三种。
1)Direct
Abaqus的Direct直接法的含义将接触中的约束关系直接加入到能量表达式中,如果接触较硬(譬如硬接触或者接触力随深度急速增加的问题)采用约束乘以Lagrange因子方法插入的方式,如下所示:



此方程是关于u和p的迭代量的一个线性方程组,看起来是两个方程求解两个未知数,但在这边K22=0,此时无法直接缩聚掉接触力项,给线性方程组求解增加难度,常用算法中迭代法需要主元非0,高斯消元法对角占优的矩阵更容易求,这也是同等维度下有限元相比边界元更容易求解方程的原因,因为有限元得到的线性矩阵都是对角线附近的非零元素,而边界元是满阵,如果主元=0,必须经过多轮行列互换将主元=0的放最下方。
而罚函数法则无以上问题。罚函数法就和我们平常生活中的惩罚的含义是一样的,小孩考了100分,奖励,考了80分,什么都不干,考了70分,罚打屁股10下,考了50分不及格,罚打屁股100下,总之,考的越差,惩罚的越多。

2)Augmented Lagrange
当然Penalty也有缺点,就是上述的K的取值是人为的,K不同得到的结果不同,而对每个模型K的取值还与接触面的刚度相关,Augmented Lagrange其实是上面两者的结合,显然,这种方法计算效率相对更差,在此不详述了。
如果是切向摩擦力,Abaqus可选择6种,其中也包括Lagrange乘子和Penalty方法。至于具体的算法介绍和适用范围可看USim大神的总结:
https://www.jishulink.com/content/post/1786826
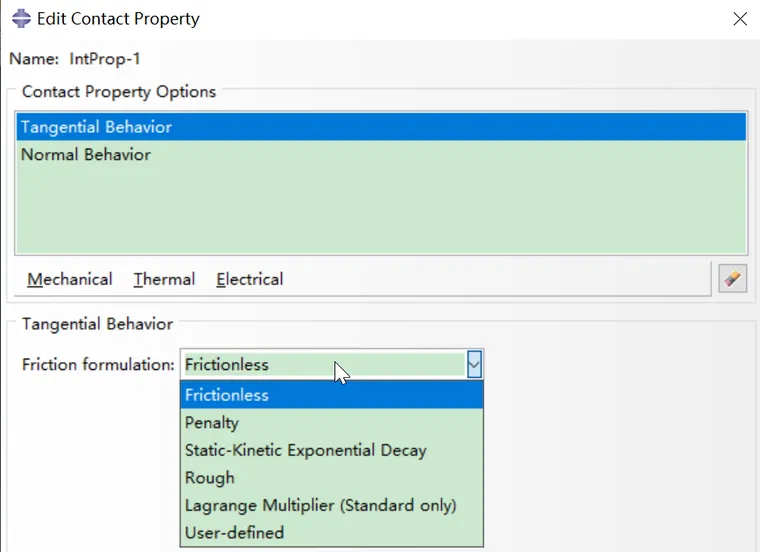
这两个方向的接触力中,共同点是都可以选择Lagrange法和Penalty法(罚刚度法),这也是接触分析中最常用的两种方法。下面我们将以一个简单的接触分析的算例来说明理论和Abaqus实际中的应用。
Abaqus中创建一个杆和一个刚性板接触的例子。


杆沿x轴方向,左端简支,刚性板与x轴成45度,固定在空间中,开始时杆的右端正好和刚性板接触,在杆上加一个往右的拉力,由于杆的右端无法穿过刚性板,只能往上沿着刚性面移动,且移动的位移u1和u2必然相等。也就是约束关系是:


参数如下:
>尺寸:Truss 长度L0=1,截面积A=1。
>材料:Young’s Modulus Em=10, Poisson Ratio 0。
>边界:左侧节点固支。
>载荷:右侧节点加集中力F=1。
>接触:设置杆靠近刚性板的一点和刚性板发生接触
>网格:划分为一个Truss单元。
>分析步:静力分析,打开NLGeom几何非线性。


Abaqus中设置接触,切向无摩擦,法向采用Direct算法:
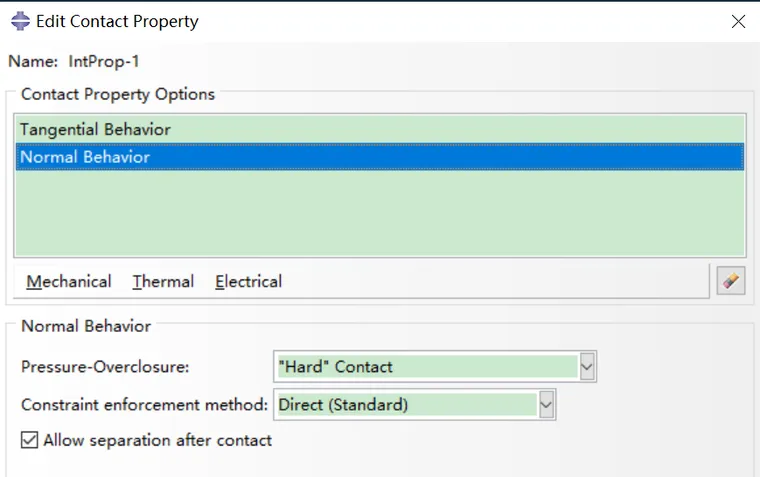

分析后得到:


可发现U1=U2=1.024e-1,和理论没有任何差异。


这个方程组的解和K相关。
当K=10时,可得:
u1=0.1036
u2=0.0956
有兴趣的可以把这两个值带入上面的方程可发现方程成立,可以看出u1和u2不是绝对相等,明显差异比较大,也就是说Penalty方法得到的解只是近似解,当然有限元中只要K足够大,那么这个误差依然可以接受。
Abaqus中设置接触,切向无摩擦,法向采用Penalty算法,且设置stiffness=10:


分析后得到的位移如下:


U1=1.047e-1,U2=8.968e-2,明显和Penalty方法理论值有较大差异,要么Abaqus的Stiffness的含义和理论的罚刚度不同,要么就是接触分析的迭代导致了和理论的差异,哪位大神要了解,欢迎讨论。
如果Stiffness=100,分析后如下,显然U1、U2更加接近0.1024这个实际问题的理论解。
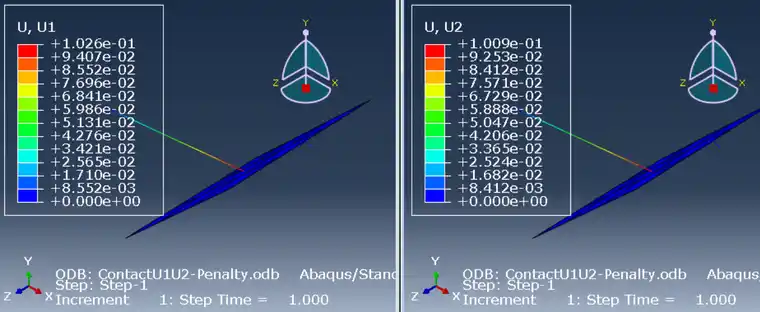

如果觉得上面的文字太复杂,也可以看一下视频的简要讲解和软件演示,地址如下:
https://www.jishulink.com/college/video/c12884


本文从接触分析时如何将接触的约束加入到有限元基本方程出发介绍了商软中最常用也是最基本的两个算法Lagrange和Penalty方法,可以看到Penalty方法中stiffness刚度的选取不同对最终的求解具有较大的影响,我们想要对标Abaqus实现Abaqus完全一致的接触分析结果,但苦于找不到Abaqus个罚刚度的选取规则,如果有哪位大神对这个问题比较了解,还请不吝赐教。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删