先来看个例子一个悬臂梁，左端固定，右端施压，求变形的问题。

已知材料弹性模量E=200GPa=2e5 MPa，压力F=500N，杆长L=100mm，杆截面为矩形，厚h=10mm，宽b=10mm，求变形WB。

翻出吃了多年灰的材料力学，查到公式为：

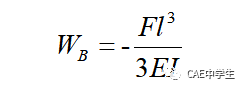
I为横截面惯性矩，对于矩形

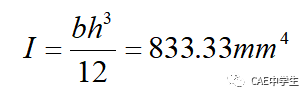
则梁的变形为：

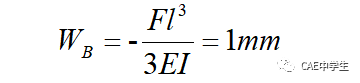
下面在Workbench静力学中计算这个案例。

Step1 建立算例与模型。

过程略，由于WB材料库中的结构钢得弹性模量为200GPa，所以本例无需修改。

Step2 网格与边界条件。

在长度方向划分10等分，厚度和宽度方向2等分。

网格使用无中节点的低阶单元，检查单元，全部为8节点的6面体单元。

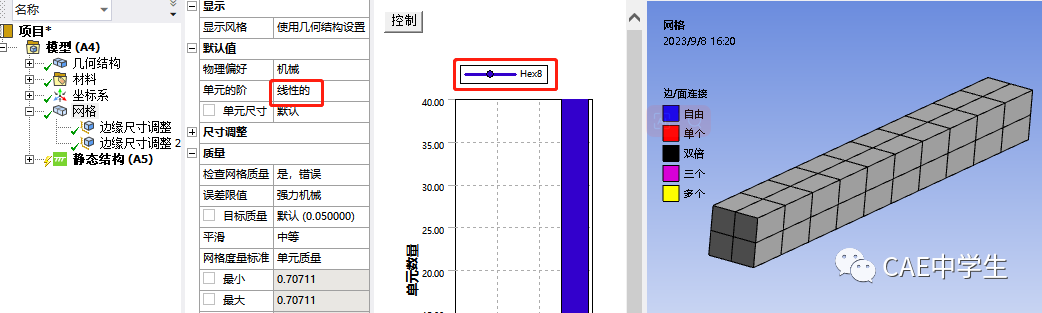
左端固定，右端施加Y正向500N的力。

Step3 计算位移。

计算求得Y向最大位移为0.984，误差1.6%可接受。

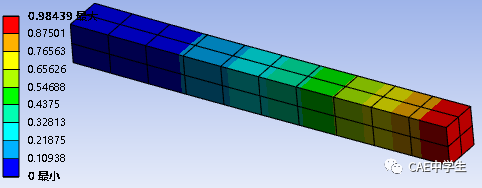
以上计算中，默认积分选项的低阶单元并没有出现剪切自锁，具体原因在下篇文末解密。

如果您第一次听到这个概念，可以暂时把剪切自锁理解为结构变硬、弯曲变形困难现象。

下面我们来验证完全积分的低阶6面体单元是否会出现剪切自锁。

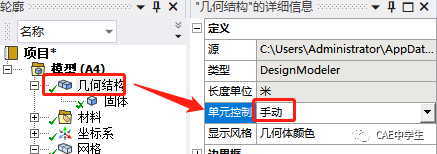
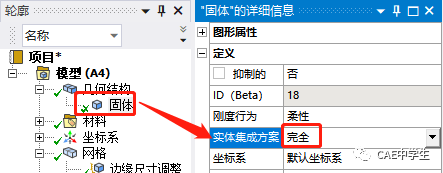
Step4 完全积分的低阶线性单元剪切自锁验证

要修改单元的积分方案，需要修改模型属性。先修改几何结构的单元控制选项为手动，这样程序才会激活积分选项。然后修改模型积分方案为完全积分。

其他条件不变再次计算，结果如下

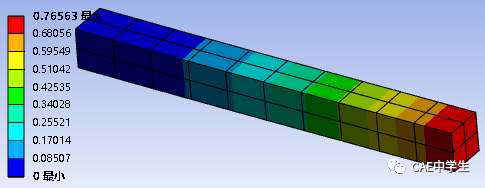
计算得Y向最大位移0.77，产生了23%的误差。

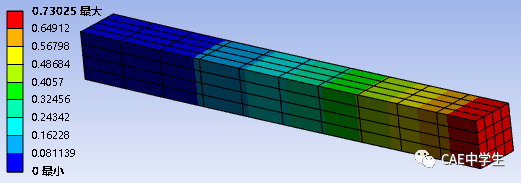
那么，网格加密后会改善吗，我们将厚度和宽度方向划分4等分，再次计算结果如下。Y向最大位移变化不大，出现27%的误差，说明加密厚度方向的网格无法预防剪切自锁。

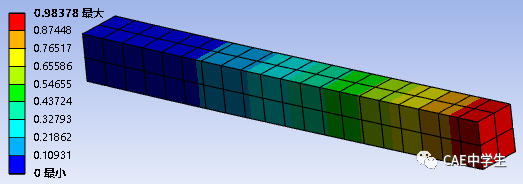
把厚度和宽度方法只划分2等分，长度方向划分20等分试试。计算得最大位移已经很接近解析解了。

结论：

1. 完全积分的低阶单元在弯曲过程中会出现剪切自锁，要消除剪切自锁现象，需要将单元改为高阶单元（完全积分与缩减积分都可以），或者加密完全积分的低阶单元的弯曲方向网格。

2. Workbench默认积分方式的低阶单元和高阶单元都不会出现剪切自锁现象。

下面就来说说剪切自锁是什么。

1 单元积分

要说到剪切自锁，就必须说到单元积分技术。

在有限元计算中，自由度{∆u}解是通过节点求出的，而应变（及应力）是在积分点求出的，然后再外推（线性计算）或者复 制（非线性计算）到对应的节点上。这种基于位移自由度的积分点遵循高斯积分法且与单元的阶数相同，即称之为完全积分。

∆ε = B∆u （B是应变-位移矩阵）

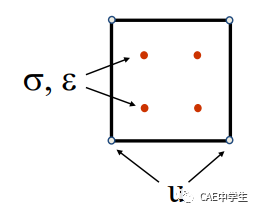
单元的积分点是由积分公式求得。举个栗子，plan182低阶平面单元和plan183高阶平面单元，完全积分点通过以下公式求得。

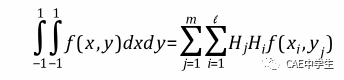
看不懂没关系，积分点位置示意如下图，左为plan182，右为plan183。

更多积分点位置见ANSYS帮助文件——Mechanical APDL——Theory Reference——12.2. Integration Point Locations。

2 剪切自锁

完全积分可解决大多数问题，但是完全积分的低阶单元会出现剪切自锁。

剪切自锁是指单元弯曲过程中的过度刚化，导致计算出的剪切应力过大，弯曲变形过小。

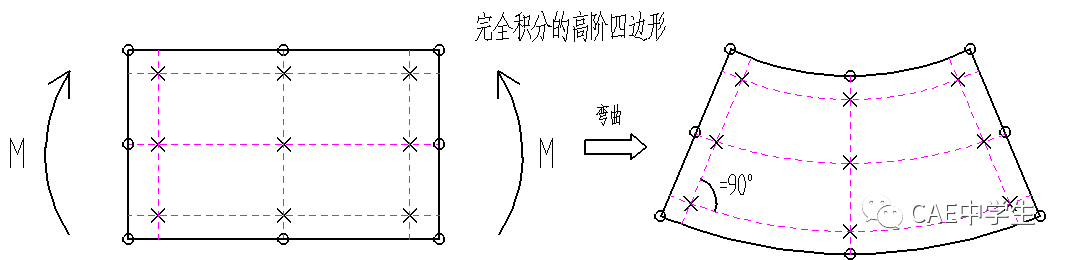
如下图，o为节点，x为积分点，在纯弯曲中，高阶单元由于有中节点，允许上下边弯曲为圆弧，过积分点的水平线与竖直线保持直角，剪应力为0，符合实际情况。

而低阶单元由于没有中节点，变形后上下边仍为直线。过积分点的水平线与竖直线不为直角，产生剪应力，使得计算的弯曲变形明显偏小，即结构刚度过大导致变形困难。

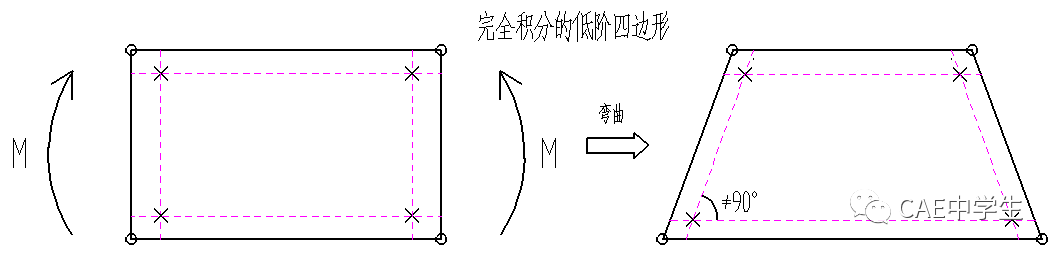
完全积分的高阶单元只有在复杂应力状态下才会出现剪切自锁，工程师应该很少遇到。

3 缩减积分

为克服剪切自锁与体积自锁，就引入了相应的单元技术，缩减积分就是其一。缩减积分比完全积分在每个方向上少用一个积分点。下图所示为平面单元缩减积分示意图。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删