本例是一个矩形长条,整体以1m/s速度向上运动,固定其左端,研究它的沙漏影响。

下面在Workbench-LSDYNA中计算这个案例。
Step1 创建算例
双击Toolbox中的 LS-DYNA即可新建算例A。
右击第2行【Geometry】——【New DsignModel】,进入DM窗口。
点击【Create】——【Primitives】——【Box】,设置长宽高分别为0.5m×0.1m×0.2m的长条。点击generate生成。退出DM。
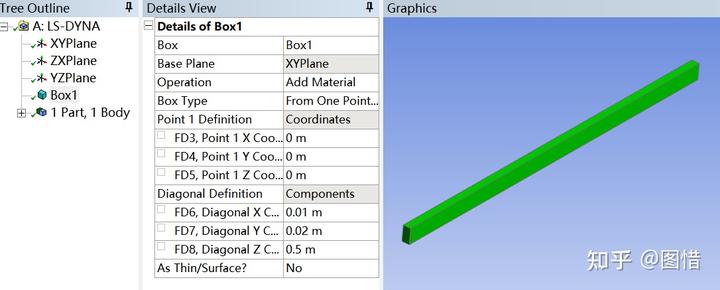
Step2 网格划分
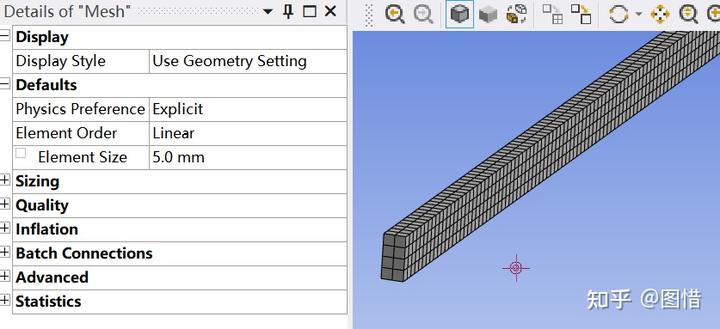
进入mechanical中,给模型整体网格设置为5mm,划分网格。此模型在LS中默认采用缩减积分的低阶六面体网格,每个六面体单元只有中心的一个积分点。
Step3 边界条件
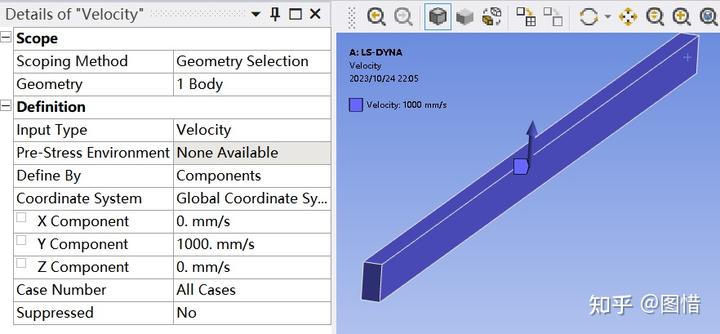
(1)设置初始速度
在结构树中右击【Initial Conditions】——【Insert】——【Velocity】,设置沿全局坐标Y方向的1000mm/s的初速度。
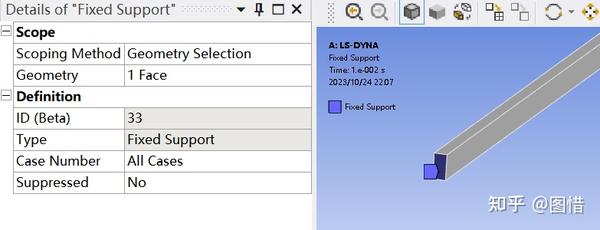
Step4 计算与设置
设置计算时间为0.01。
设置全局沙漏控制方法为Standard LD-DYNA(ID=1),沙漏系数默认为0.1,如此设置是为了故意调出沙漏模式。

在结构树中右击【Initial Conditions】——【Solve】开始计算。
Step6 后处理
计算后可插入内能、沙漏能:在结构树中右击【Solution Information】—【Insert】插入。
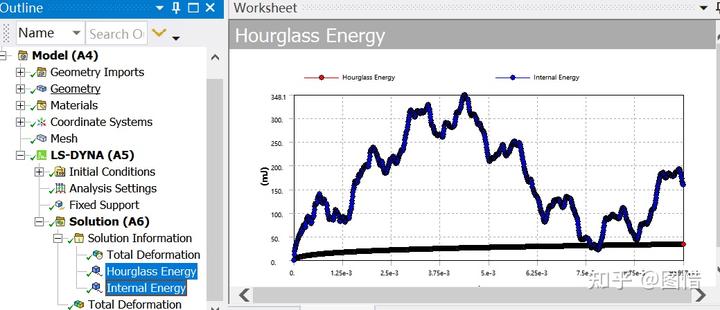
同时查看内能与沙漏能,发现沙漏能为33.6mJ左右,大于内能的10%,有些时候甚至超过内能,说明计算结果不可信。
改进方案2:使用沙漏控制ID=4~7。
在计算设置中,将沙漏控制改为4~7中任意一种,沙漏系数默认0.1不改。重新计算。

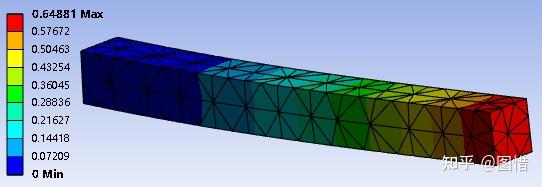
沙漏能与内能如下图,沙漏能明显减小了,为2.6mJ左右,小于内能的5%。
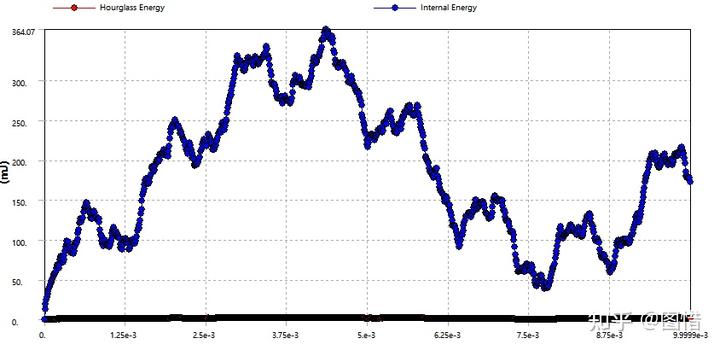
下面就来说说沙漏现象是什么。
沙漏又称为零能量,是指在只有一个积分点的低阶四边形或六面体单元中,当发生弯曲时,过积分点的水平线与竖直线的长度均未发生变化,夹角也没有变化,即此积分点未获得任何单元应变能,即所有的应力分量都是零,不具备刚度,也无法抵抗变形。
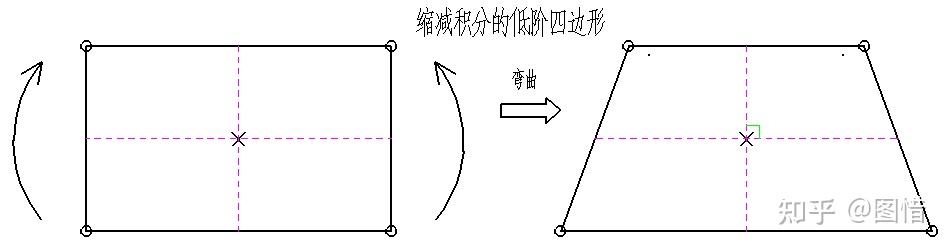
如果把剪切自锁称为“刚度过硬”现象,那么沙漏模式可以理解为“刚度过软”。
在粗网格中,这种零能模式会通过网格扩散出去,产生无意义的结果,即沙漏模式。沙漏模式出现于缩减积分的情况下,通常只是低阶单元中的问题。
缩减积分的高阶单元一般不会出现沙漏模式。引用帮助文档的原文:如果模型对于 2D 问题至少有两个(高阶)单元,或者对于 3D 问题每个方向至少有两个(高阶)单元,则沙漏效应不是问题,因为沙漏模式很难传播到一个元素之外。因此不需要沙漏控制。
梁、三角形、四面体等单元没有沙漏模式。但是低阶四面体/三角形的刚度偏大,会导致变形偏小,需要细化网格或更换为高阶单元。比如上一篇文章的案例使用低阶四面体单元,厚度两层单元,位移比解析解少了35%左右。
ANSYS里面的18x系列单元叫做现代技术单元,会自动选择单元技术来解决剪切和体积自锁。
如何验证程序自动选择了单元技术呢?
还是使用上篇文章的静力学案例,将几何结构的单元控制改回程序控制(学习在于反复折腾)。
厚度和宽度划分2分,长度划分10分,低阶单元。
重新计算,得到接近1mm的位移解。

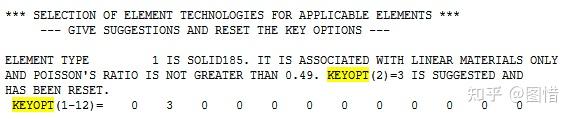
在求解信息中搜索keyopt字样,如下图。这段话意思是:***适用单元的单元技术选择***——给出建议并重置关键选项——单元类型1,Solid185单元。它与线性材料相关并且泊松比不大于0.49,建议使用Keyopt(2)=3并已重新设置。下面给出了keyopt1~12关键字的各自取值。
在帮助文档搜索solid185,查看其单元技术。关键字keyopt(2)=3表示简化的增强应变,用于防止弯曲问题中的剪切锁定,以及体积问题中泊松比≤0.49的模型的体积锁定。这就不难理解,为什么程序控制下的默认积分选项不会出现剪切自锁等现象了。

而至于为什么低阶六面体/四边形单元,在默认积分下不会出现沙漏的原因,那就更简单了,因为它们在WB静力学中默认使用全积分(B方法),而在LSDYNA中使用了沙漏控制技术。比如本例的单元技术完整表述是:采用了B方法完全积分,附加选用了简化的增强应变。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删