产品
一、背景介绍
为了提高风能利用效率，增加单位时间内风力发电数量，海上风电塔向着叶轮更大、高度更高的趋势发展。如图1所示，2010年我国风电塔总高度在90m左右，到2020年，风电塔总高度上升至220m，预计到2025年，海上风电塔装机容量可达15~20MW，高度可达240m以上。
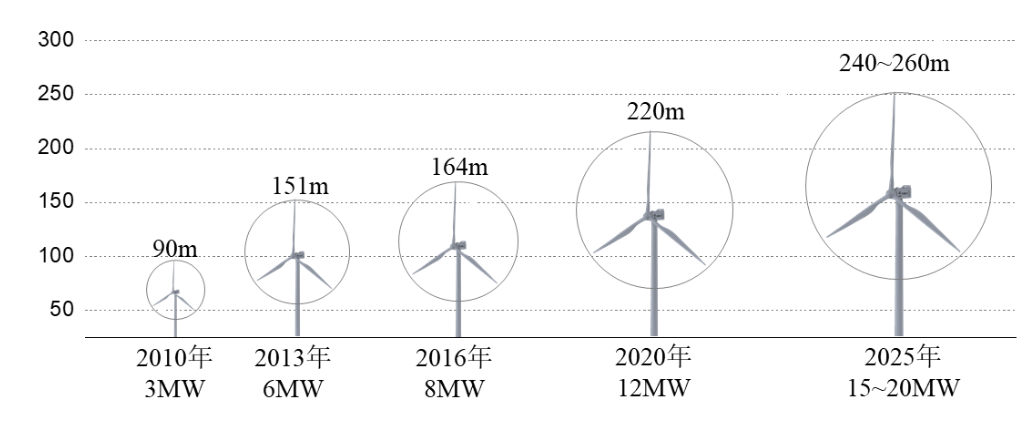图1海上风电塔发展趋势
单桩式海上风电塔属于较为敏感的高耸薄壁结构，因其高度较高，支撑结构径厚比较大，因而具有较大的柔性。因此，在地震作用下极易发生风机停机或倒塌破坏。
图2 单桩式风电塔
单桩式风电塔支撑结构为锥形塔筒，塔筒顶部直径3.07m，底部直径4.5m，顶部塔筒厚度20mm，底部塔筒厚度50mm。塔筒分上段塔筒、中段塔筒、下段塔筒三部分，材料为Q345B钢材，塔筒具体结构参数如上图所示。
二、风机有限元建模
采用ABAQUS建立风机整体有限元模型，结构与土相互作用采用假想嵌固点法。
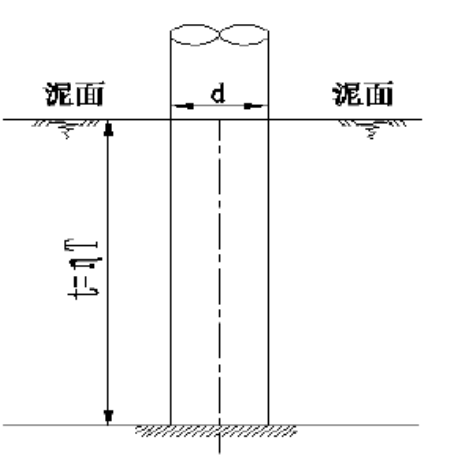
图3嵌固点示意图
风电塔筒为锥形，分上、中、下三部分，在ABAQUS中利用旋转命令建立锥形塔筒模型，打开草图绘制界面，依次输入图示坐标点，点击完成，进行塔筒部件的创建。桩基础按照假想嵌固点法，截取12.346m钢管桩并将底部固定，材料为Q345钢材，网格采用C3D8R实体单元。
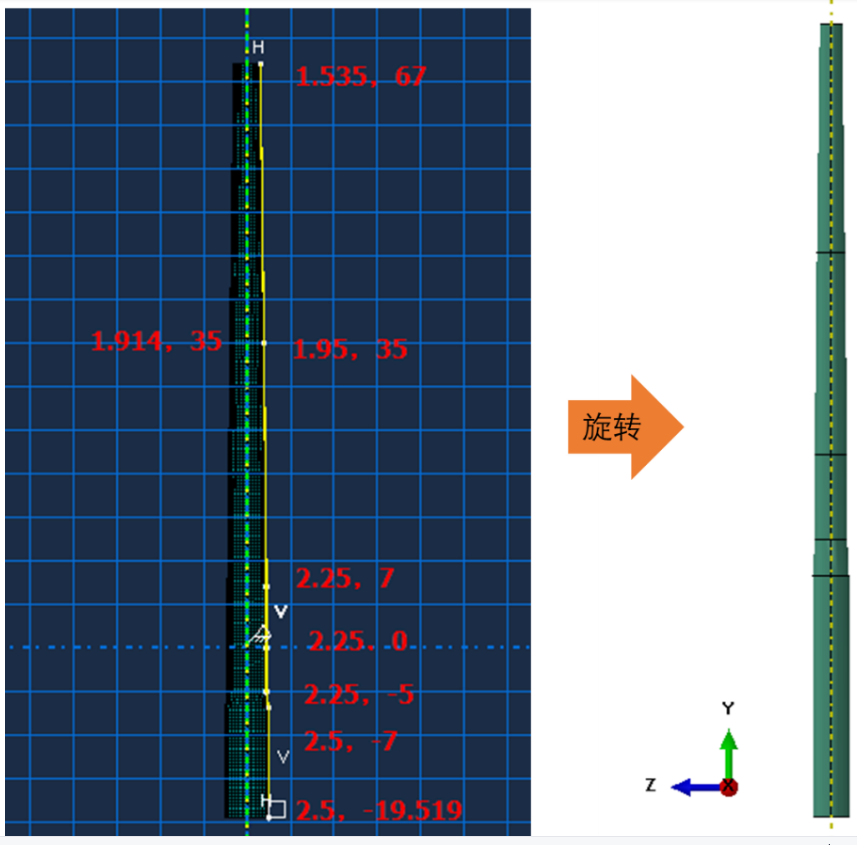
图4 塔筒部件建模
上部结构包括机舱、轮毂及叶片，机舱内主要为齿轮箱、发电机等，在建模时将机舱及轮毂简化为整体结构，且不考虑其塑性变形，弹性模量按照钢材输入206GPa，材料密度按照机舱总重进行等效机舱总质量为131.427t，等效密度为361kg/m3。叶片由玻璃复合纤维材料制成，计算时不考虑其塑性破坏，其弹性模量为28GPa，泊松比0.3，密度为66.18 kg/m3。叶片、轮毂及机舱之间采用“Tie”约束。网格划分时，叶片及轮毂采用C3D10单元，机舱采用C3D8R单元，风电塔整体有限元模型如图5所示。
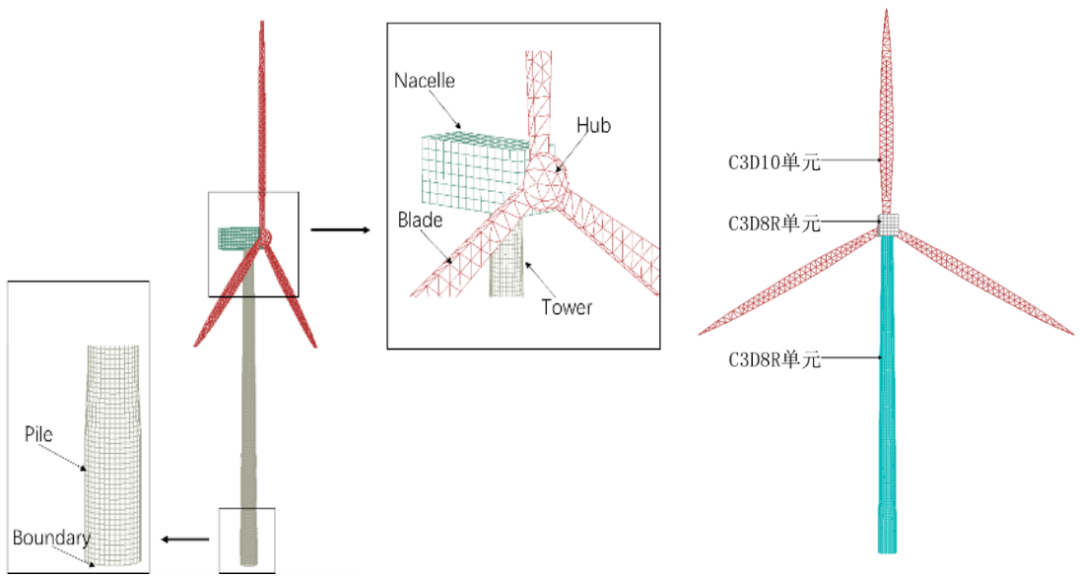
图5风电塔整体结构有限元模型
三、地震加载
按照日本《道桥示方书》《建筑抗震设计规范》GB50011-2010的相关规定，选取El Centro、Nihonkai-Chubu、Hyogoken-Nanbu三种不同类型地震动作为数值模拟输入地震动。将所选地震记录调整为不同的PGA值(0.07g、0.2 g、0.40 g)，对于El Centro和Nihonkai-Chubu地震，仅考虑水平地震动输入，对于Hyogoken-Nanbu地震，考虑水平地震动和竖向地震动的双向输入，按照规范要求，竖向地震加速度峰值取水平峰值的0.65倍。
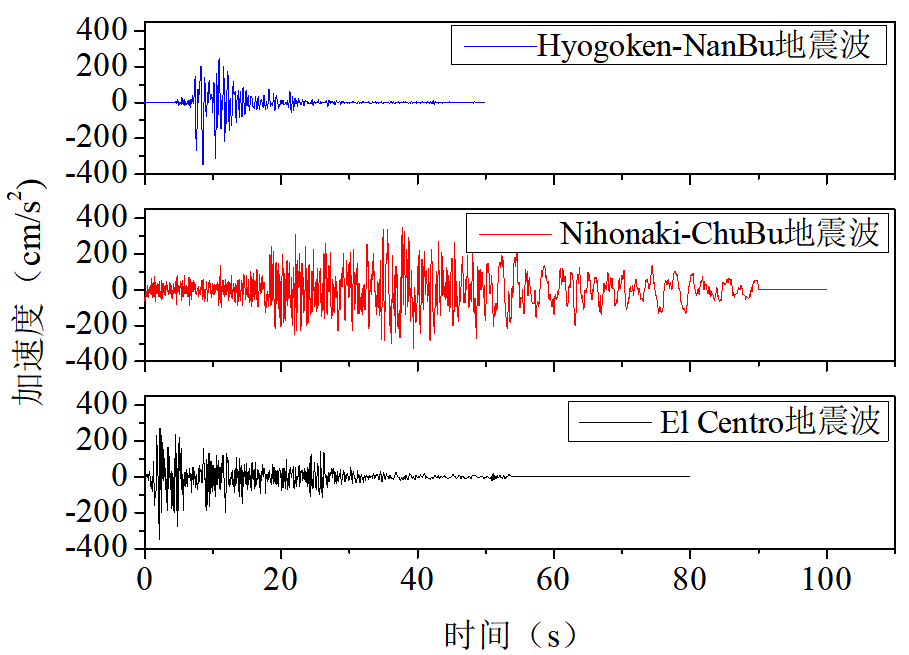
图6地震动加速度时程曲线
在分析步设置中创建重力分析步Step-1和动力隐式分析步Step-2，重力加载时间为1s，地震加载时间按照所选取的地震波时长进行更改。
图7 分析步设置
在ABAQUS中，取消塔筒底部X方向平动自由度约束，并在X方向添加加速度激励，加速度幅值曲线选取相应地震波。
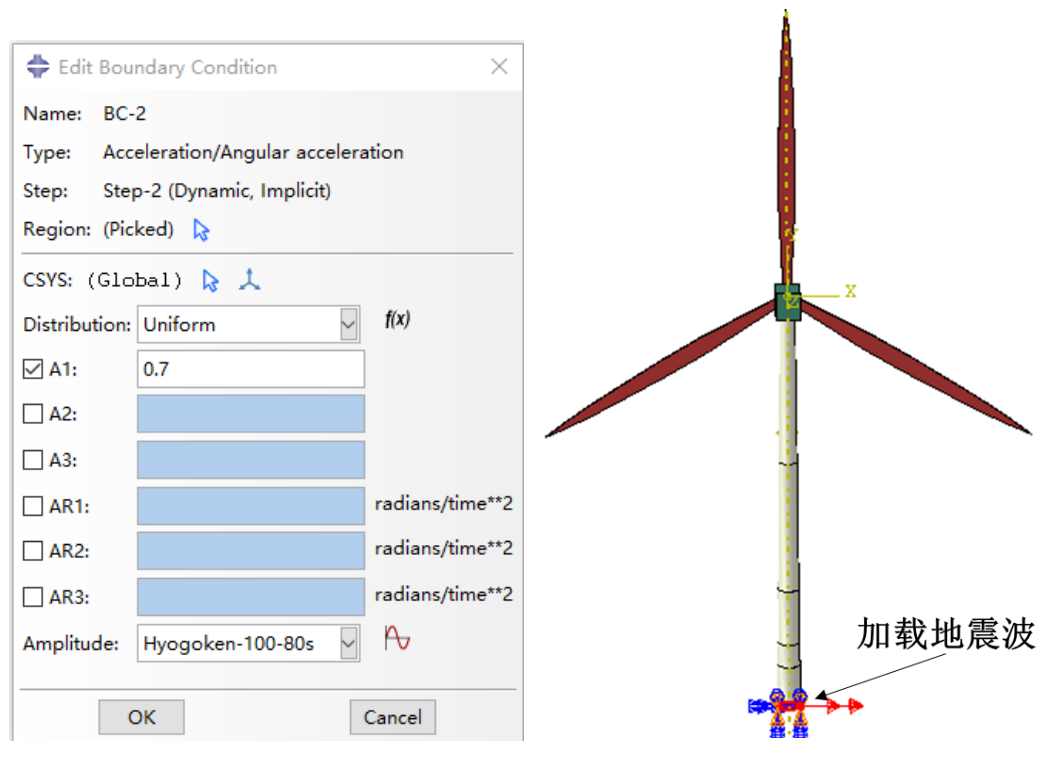
图8 地震加载设置
四、结果对比
在El Centro地震作用下，当PGA=0.07g、0.2g和0.4g时，风电塔顶部位移最大值MDT（The Maximum Displacement of the Top）分别为0.051m， 0.122m和0.245m，地震峰值加速度增加分别导致结构MDT值增加136%和378%，且峰值出现时间不同；在Nihonkai-Chubu地震作用下，三种峰值加速度下结构的顶部位移分别为0.211m， 0.493m和0.989m；在Hydrogen地震作用下，结构MDT值分别为0.031m， 0.085m和0.170m；比较以上结果可以看出，El Centro地震作用下结构出现最大位移的时间存在变化，但是其他两类地震作用下结构最大位移值未发生变化。
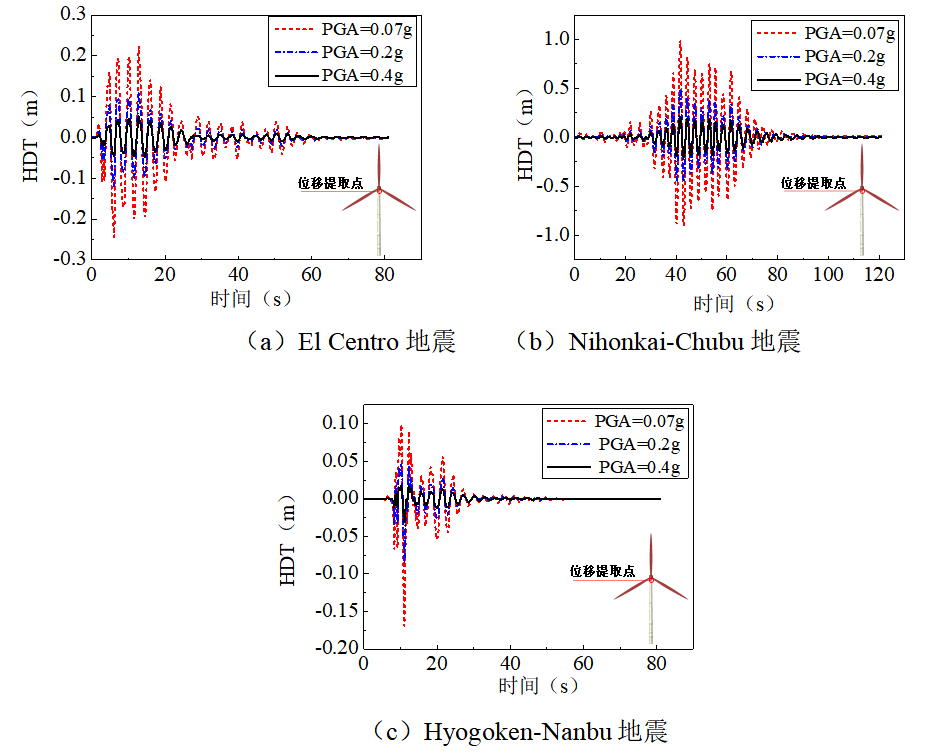
图9风电塔结构顶部位移时程曲线
从上述结果中可以看出，近场地震和远场地震对风电塔这种高耸薄壁结构的影响差别较大。由于远场地震卓越频率与风电塔自振频率接近，因此在远场地震作用下的加速度及位移响应值更大，但近场地震PGA的增加对结构响应的变化幅度影响更大。
三种地震作用下PGA=2g时的结构破坏形态，如图10所示。由图可知，在El Centro及Hydrogen地震作用下，结构均表现为塔筒顶部弯曲过大导致上部结构倒塌，在Nihonkai地震作用下不仅塔筒顶部出现弯曲破坏，在塔筒与桩基础相交处也出现了屈曲和塑性变形。由此可知，远场地震作用对于风电塔结构的破坏性更大。
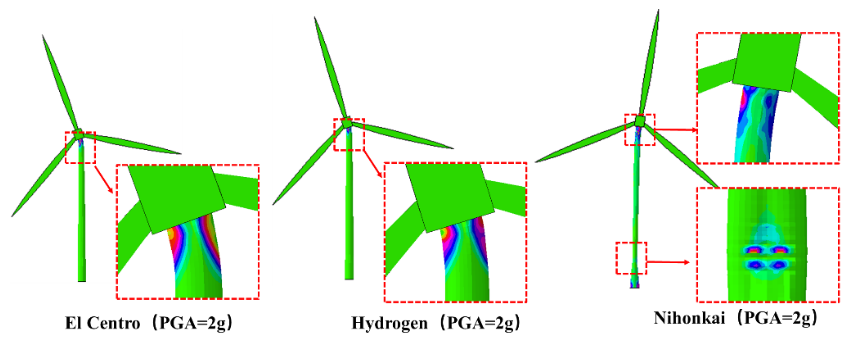
图10 不同地震作用下结构的倒塌形式
由于本论文尚未发布，以上的模型暂不公开分享。但笔者可分享一个类似的模型供大家练习。欢迎文尾点赞和在看，截图发到本***回复 单桩式风电机模型
，24小时获得以下模型资料，更多内容请关注下文风力发电仿真学习包。
免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删
155-2731-8020
