FLUENT垂直空心圆柱自然对流传热计算

1 前言

今天，我们继续做一个垂直实心圆柱的自然对流传热计算，这些案例都是经典的自然对流案例，有大量的实验数据和理论推导公式进行表面努塞尔数的计算，可以用于设备绝热设计计算。

2建模与网格

一个钢制实心圆柱垂直放置于20℃的空气中，圆柱直径D=40mm，高度L=40mm，采用二维轴对称模型建立如下计算域。其中，圆柱实体不建模，只建立空气域，计算域边界的选取：高度H=24D+L，宽度W=5D。划分全四边形网格，节点数约5万。注意对于轴对称模型，FLUENT需要将对称轴放在X轴上，计算域需要处于正Y轴区域。

3基本定义

以圆柱高度L为特征长度，基于特征长度的瑞利数、格拉肖夫数分别按下列式计算。

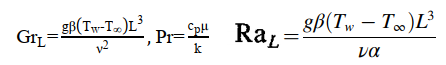
4边界条件与求解设置

空气的温度为20℃，其物性参数如下。

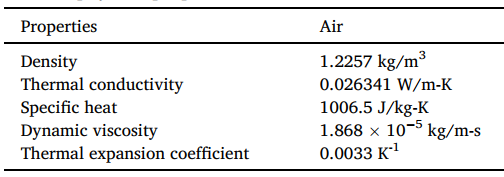
计算域各边界条件为：空气域底部为绝热光滑无滑移壁面，顶部和侧边均为压力出口边界，表压0Pa，回流温度20℃。圆柱顶部和侧边为光滑无滑移壁面，其中侧边为恒温边界，顶部分别设置为恒温壁面（同侧边温度）和绝热壁面，计算两种顶部边界的努塞尔数；

空气的密度根据上述物性参数采用boussinesq模型，提高收敛性，也可考虑用不可压缩理想气体模型，但是收敛性可能不如前者。

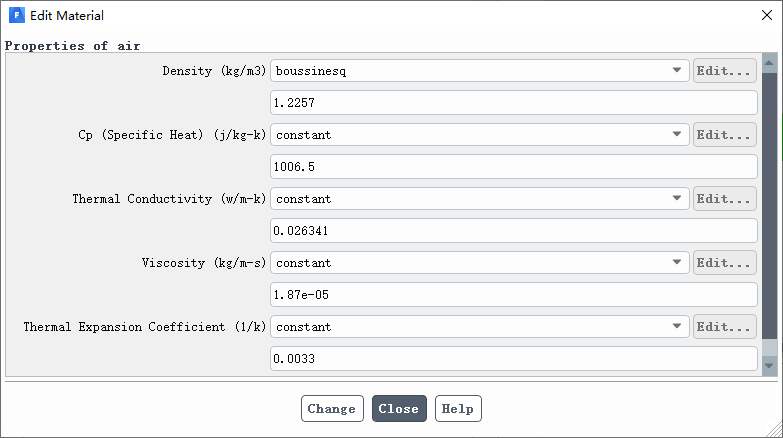
采用boussinesq模型时，由于计算域是开放式的，操作密度和操作温度都取空气的物性值。设置重力加速度，注意如前述轴对称模型的特殊要求，重力加速度要设置在X轴上。

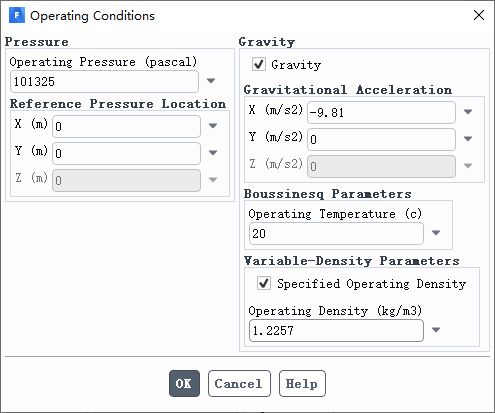
其他求解设置采用默认，稳态求解。

5计算结果

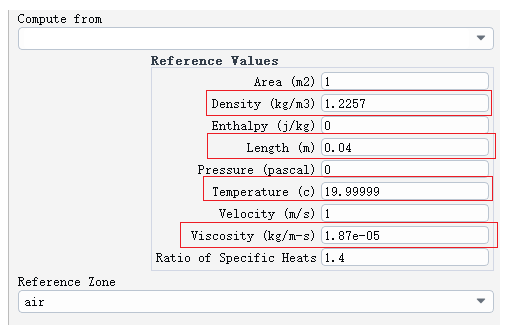
由于要计算努塞尔数，参考值的设置非常重要，该案例通常取空气参数作为参考值，参考长度即为特征长度，下列框选项为计算努塞尔数时需要设置的参考值。

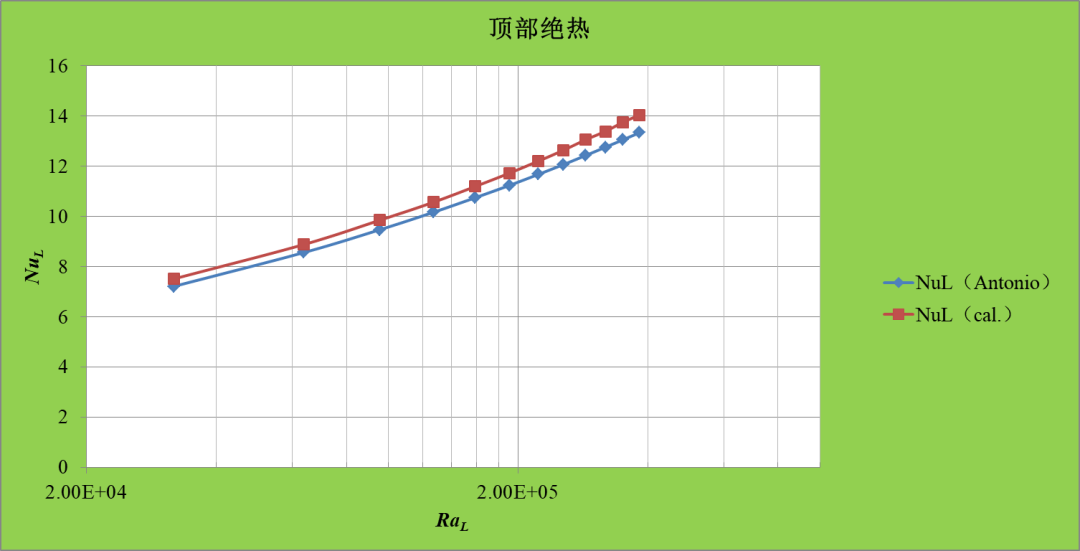
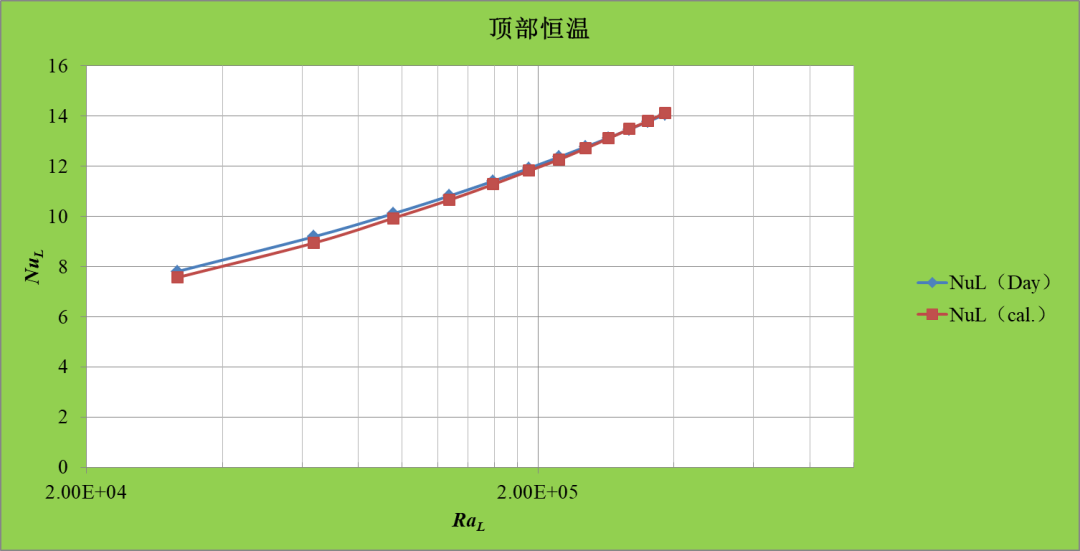
我们看一下不同瑞利数下，基于特征长度的努塞尔数计算结果，这里针对圆柱顶部绝热边界和恒温边界分别作了计算，将计算结果同参考文献结果对比分别如下，参考的结果有的是数值计算拟合的公式，有的是基于实验数据的经验公式。可以看出，本案例的计算结果和参考文献结果相近。

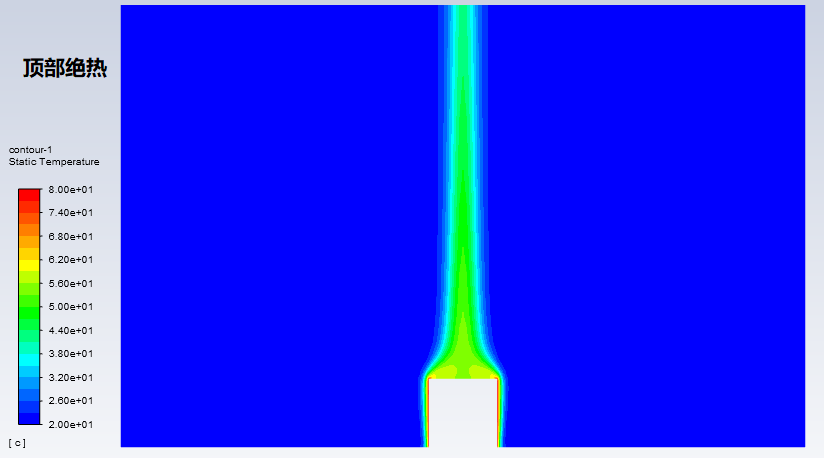
再看一下其中某个瑞利数下，顶部绝热和恒温边界下的温度分布，可以看出顶部恒温时，靠近圆柱顶部的空气温度比绝热条件显著更高。

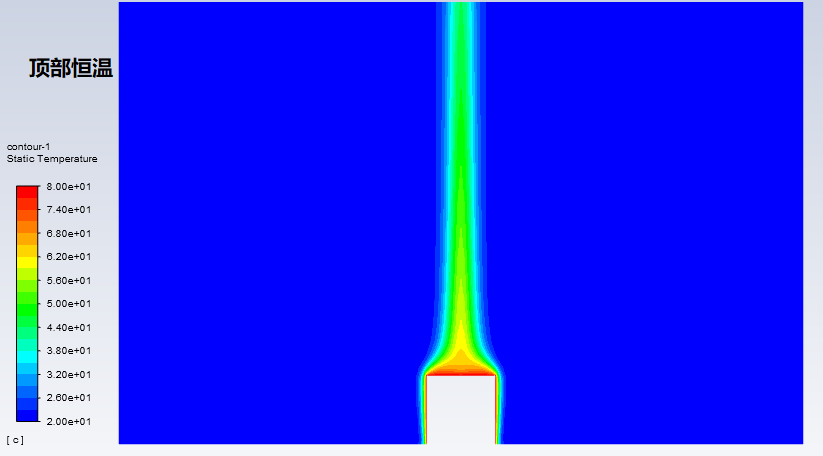
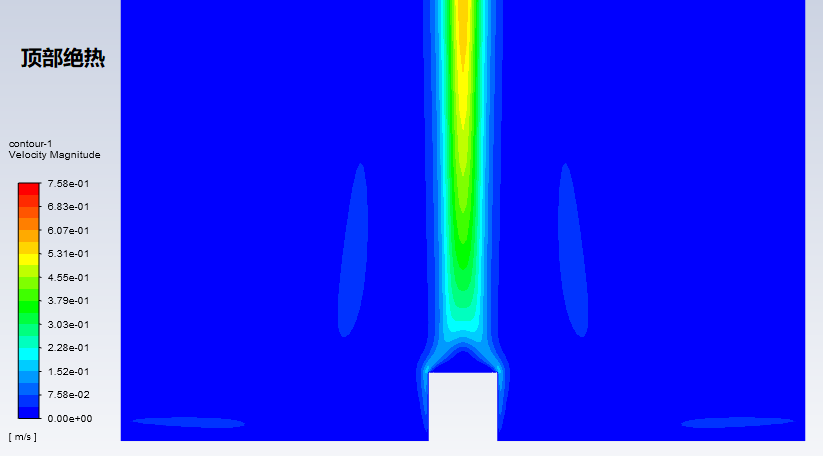
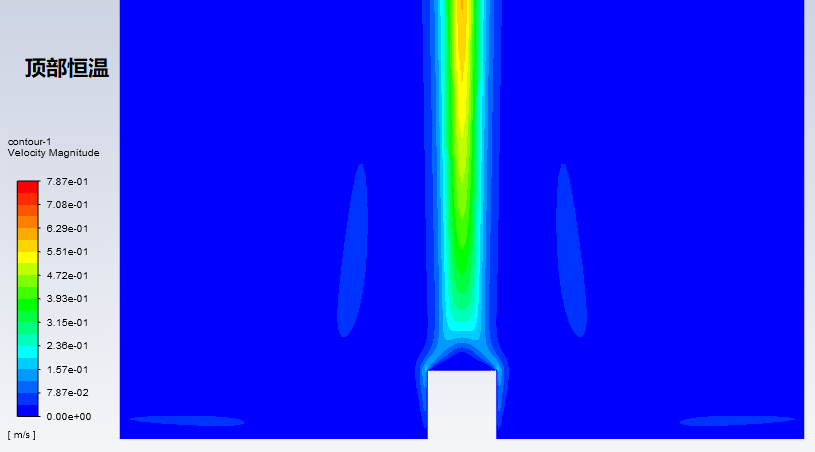
最后看一下其中某个瑞利数下，顶部绝热和恒温边界下的速度分布，由于圆柱上方被加热得更剧烈，顶部恒温条件下，空气域的最高速度略高于前者。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删