
复合材料是一种多相材料,由多种性质极不相同的材料组成。先进的复合材料在本世纪60年代初才发明,较具代表性的为聚合物为基的高性能的碳纤维和硼纤维复合材料。
复合材料性能的可设计性,是复合材料所特有的主要优点。纤维复合材料是由两种或两种以上不同强度和模量的材料所构成,在纤维和基体材料选定后,尚有许多材料参数和几何参数可变动,而且形成层合结构时每一层的铺设方向又可随意安排,这样就可以人为的改变组分材料的种类、含量,以及铺层方向和顺序,本文研究了不同铺层方式对其力学性能的影响规律。
模型的建立与计算
如图1所示,给出了层合板的有限元模型,在ansys有多个单元可以模拟复合材料,本文选取SHELL99单元来模拟层合板这个力学模型。本文的层和板共分为四层,每层的厚度为0.002m,长度和宽度都为0.25m。

图1 层合板的有限元模型

图2 层合板的有限元模型的载荷
本文的模型的计算边界条件:四边固定;在面上受到均匀的压力其大小为1e5pa。表1给出了复合材料的性能参数。

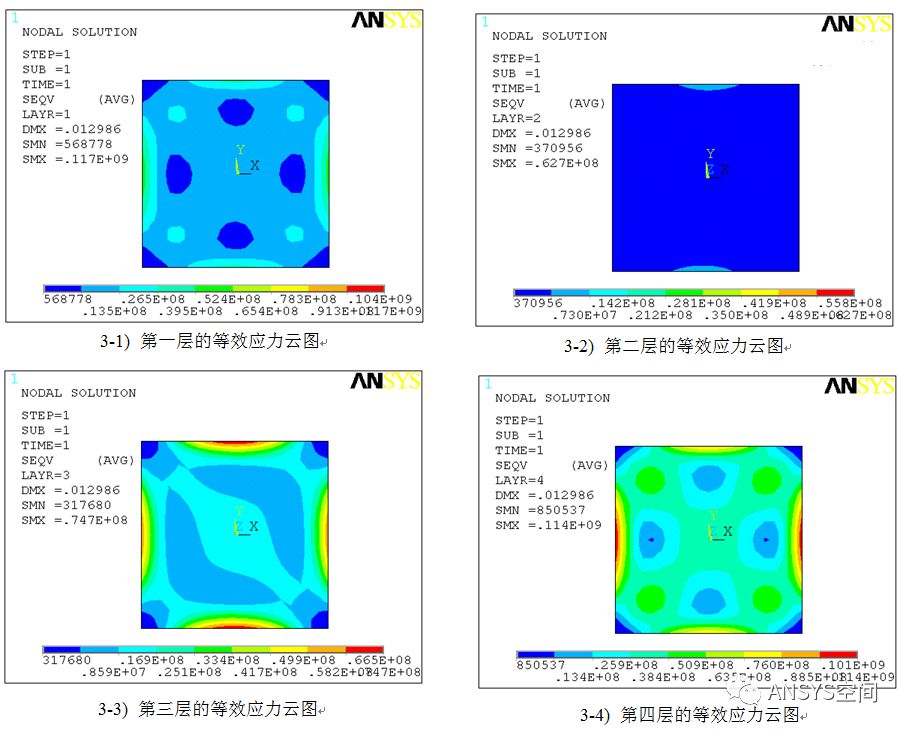
图3 铺层方向0/90/45/0的各层的等效应力
图3给出了铺层方向为0/90/45/0的各层的等效应力。由图可知:第一层的更大等效应力为0.117E9Pa;第二层的更大等效应力为0.627E8Pa;第三层的更大等效应力为0.747E8Pa;第四层的更大等效应力为0.114E9Pa。从以上数据可知:层合板的第一层和最后一层的应力更大,第二层的应力最小。
图4给出了铺层方向为0/45/45/0的各层的等效应力。由图可知:第一层的更大等效应力为0.114E9Pa;第二层的更大等效应力为0.739E8Pa;第三层的更大等效应力为0.749E8Pa;第四层的更大等效应力为0.114E9Pa。从以上数据可知:层合板的第一层和最后一层的应力更大,第二层的应力最小。
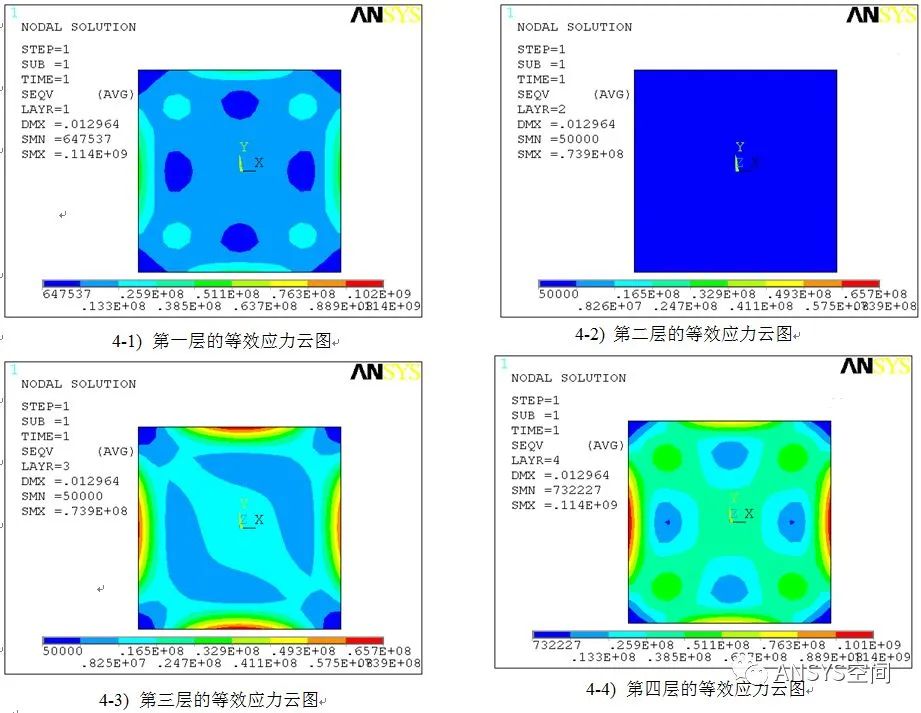
图4 铺层方向0/45/45/0的各层的等效应力
图5给出了铺层方向为0/90/90/0的各层的等效应力。由图可知:第一层的更大等效应力为0.117E9Pa;第二层的更大等效应力为0.635E8Pa;第三层的更大等效应力为0.635E8Pa;第四层的更大等效应力为0.116E9Pa。从以上数据可知:层合板的第一层和最后一层的应力更大,第二层的应力最小;铺层方向角相同的层其更大等效应力也相同。

图5 铺层方向0/90/90/0的各层的等效应力

图6 铺层方向45/-45/45/-45的各层的等效应力
图6给出了铺层方向为45/-45/45/-45的各层的等效应力。由图可知:第一层的更大等效应力为0.125E9Pa;第二层的更大等效应力为0.639E8Pa;第三层的更大等效应力为0.638E8Pa;第四层的更大等效应力为0.125E9Pa。从以上数据可知:层合板的第一层和最后一层的应力更大,第二层和第三层的等效应力最小。
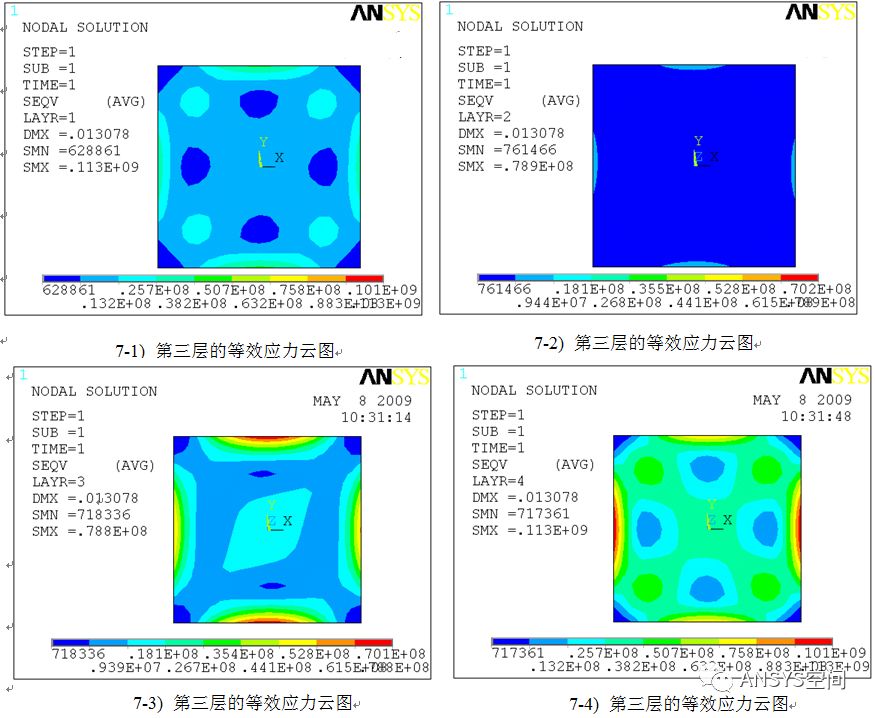
图7 铺层方向90/45/-45/0的各层的等效应力
图7给出了铺层方向为90/45/-45/0的各层的等效应力。由图可知:第一层的更大等效应力为0.113E9Pa;第二层的更大等效应力为0.789E8Pa;第三层的更大等效应力为0.788E8Pa;第四层的更大等效应力为0.113E9Pa。从以上数据可知:层合板的第一层和最后一层的应力更大,第三层的应力最小。
结论
通过以上分析和计算可以得出以下结论:
(1) ansys可以处理复杂的复合材料力学问题。
(2) 在同种载荷和边界条件下,不同的铺层方向对其应力有显著的影响,本文中铺层方向:45/-45/45/-45的等效应力更大;铺层方向为0/90/90/0的等效应力最小。这对实际的复合材料设计有一定的指导意义。
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删