与传统材料相比,复合材料具有可设计性,复合材料结构的多层次性为复合材料及其结构设计带来了极大的灵活性,复合材料的力学性能和机械性能,都可按照结构的使用要求和环境条件要求,通过组分材料的选择匹配、铺层设计及界面控制等材料设计手段,最大限度的达到预期目的,以满足工程设备的使用性能,因此,在工程实践中对复合材料结构进行优化设计有很重要的现实意义,下面以我所研究的复合材料压力容器为例,将复合材料结构优化以及在ANSYS下的实现过程给大家作一个介绍。
1. 问题描述
本文所涉及的复合材料压力容器是带有金属内胆外缠碳纤维增强复合材料的复合容器,优化问题是:以金属内胆壁厚、复合材料各缠绕层厚度和缠绕角为设计变量,在满足压力容器强度(金属内胆层和复合材料层均满足强度要求)和重量要求的条件下,使压力容器的刚度最大。
2. 优化模型
根据纤维增强复合材料特性,压力容器环向缠绕复合材料有利于提高容器刚度,轴向平铺复合材料有利于提高容器刚度,因此,模型采用3种缠绕角的方案,即靠近金属内胆为环向(90度)缠绕,中间为 缠绕,外部为轴向平铺(0度),以各层的厚度(金属层和三层复合材料)和中间缠绕层的角度为优化参数,在压力容器强度约束的条件下,以压力容器一阶固有频率为优化目标。其数学模型如下:
缠绕,外部为轴向平铺(0度),以各层的厚度(金属层和三层复合材料)和中间缠绕层的角度为优化参数,在压力容器强度约束的条件下,以压力容器一阶固有频率为优化目标。其数学模型如下:

其中,f为复合材料压力容器的一阶固有频率,s1和s2分别为金属内胆的安全系数和各复合材料层的强度比,通过有限元程序求得, 为中间层复合材料缠绕角,h1 、h2 和h3分别为金属内胆厚度、90度缠绕层厚度和
为中间层复合材料缠绕角,h1 、h2 和h3分别为金属内胆厚度、90度缠绕层厚度和 度缠绕层厚度,H为h1 、h2 和h3的极限值,当总厚度确定后,0度缠绕层厚度由h1 、h2 、h3及总厚度确定,c为复合容器重量,c0为全压力容器重量上限。
度缠绕层厚度,H为h1 、h2 和h3的极限值,当总厚度确定后,0度缠绕层厚度由h1 、h2 、h3及总厚度确定,c为复合容器重量,c0为全压力容器重量上限。
3. 优化算法
基于ANSYS的优化,可以直接使用ANSYS提供的优化模块,根据上述优化模型,建立优化计算文件,选择合适的优化算法,进行计算。
同时,也可以通过APDL语言(甚至可以通过外部编程环境,如VC++,FORTRAN等)来自己编制优化算法,本文就是通过自己编制优化算法来实现的,采用的优化算法是复形调优法。算法描述如下:
复形调优法是求解约束条件下 维极值问题的重要方法,通过构造复合形,计算各顶点的目标函数值,并进行比较,然后循环迭代,逐步替代最坏点构造新的复合形,经过多次迭代,进行收敛判断,最终得到最优复合形,并求得最优值。其迭代过程如下:
维极值问题的重要方法,通过构造复合形,计算各顶点的目标函数值,并进行比较,然后循环迭代,逐步替代最坏点构造新的复合形,经过多次迭代,进行收敛判断,最终得到最优复合形,并求得最优值。其迭代过程如下:

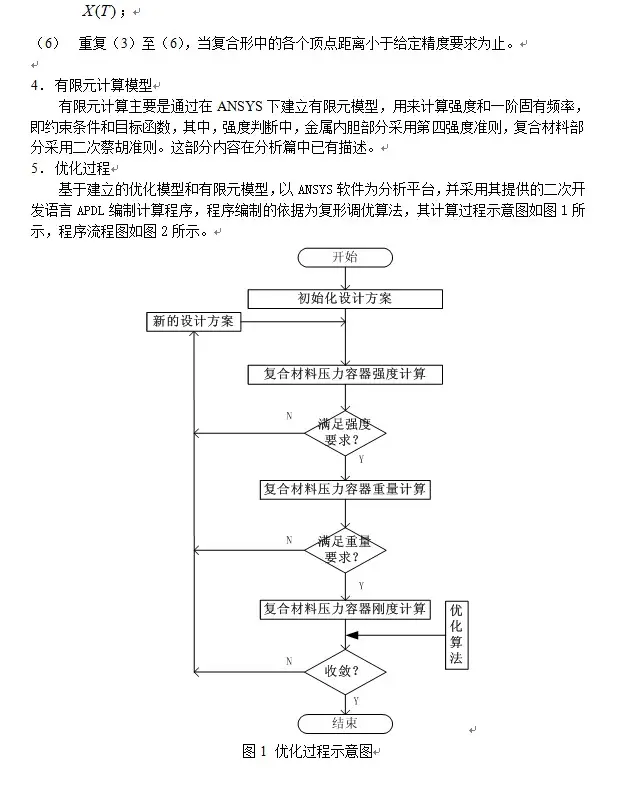

免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删