探索CFD中的多孔介质世界

1. 应用场景

在实际的工程计算中经常会遇到如：土壤，海绵，岩石，过滤器，滤网这一类的问题计算。

对于这一类介质的计算来说，其几何空隙非常多，建立真实的几何非常麻烦，且会产生非常多的网格，工作量和计算量都非常大。因此，可以简化为多孔介质进行计算。

多孔介质模型可以应用于很多问题，如通过充满介质的流动、通过过滤纸、穿孔圆盘、流量分配器以及管道堆的流动。当你使用这一模型时，你就定义了一个具有多孔介质的单元区域，而且流动的压力损失由多孔介质的动量方程中所输入的内容来决定。通过介质的热传导问题也可以得到描述，它服从介质和流体流动之间的热平衡假设，具体内容可以参考多孔介质中能量方程的处理一节。

多孔介质的一维化简模型，被称为多孔跳跃，可用于模拟具有已知速度/压降特征的薄膜。多孔跳跃模型应用于表面区域而不是单元区域，并且在尽可能的情况下被使用（而不是完全的多孔介质模型），这是因为它具有更好的鲁棒性，并具有更好的收敛性。详细内容请参阅多孔跳跃边界条件。

2. 基本原理

将流体域设置为多孔介质后，可以人为定义各个方向上的阻力系数，来代替多孔介质中的固体对流体的阻力。即添加一个与速度相关的动量汇，其表达公式为
S i = − ( ∑ j = 1 3 D i j μ v j + ∑ j = 1 3 C i j 1 2 ρ ∣ v ∣ v j ) S_{i}=-\left(\sum_{j=1}^{3} D_{i j} \mu v_{j}+\sum_{j=1}^{3} C_{i j} \frac{1}{2} \rho|v| v_{j}\right) Si​=−(j=1∑3​Dij​μvj​+j=1∑3​Cij​21​ρ∣v∣vj​)

   其中， S i S_{i} Si​ 为第i(x,y,z)方向上的动量方程的源项；v为速度值；

D 与C 为指定系数矩阵，D系数这一项代表粘性损失项，C系数这一项代表惯性损失项。

对于均匀的多孔介质来说，可改写为下面这个式子 S i = − ( D μ v i + C 2 1 2 ρ ∣ v ∣ v i ) S_{i}=-\left(D \mu v_{i}+ C_2 \frac{1}{2} \rho|v| v_{i}\right) Si​=−(Dμvi​+C2​21​ρ∣v∣vi​)

其中，

D为黏性阻力系数，又可以被改写为1/α，α为渗透率；

C 2 C_2 C2​为惯性阻力系数；v为速度

动量汇  S i S_i Si​作用于流体产生了压力梯度 D p D_p Dp​，即 D p = − S i ∗ l D_p = -S_i * l Dp​=−Si​∗l ,  l l l为多孔介质域的厚度。

压降和流速的关系是一个一元二次方程的形式 Y = A x 2 + B x Y=Ax^{2} + Bx Y=Ax2+Bx

我们在计算多孔介质区域时最重要的两个参数  D D D 和 C 2 C_2 C2​ 可以通过拟合压降和流速的关系式来求得。

例如有压降与速度关系式  △ p = 1398.8 u 2 + 1785.1 u \triangle p = 1398.8 u^{2} + 1785.1u △p=1398.8u2+1785.1u

于是有:

1398.8 = C 2 1 2 ρ ∗ l 1398.8 = C_2\frac {1}{2}\rho*l 1398.8=C2​21​ρ∗l, 根据流体密度和滤网(多孔介质)的厚度可以计算得到惯性阻力系数 C 2 C_2 C2​

1785.1 = D ∗ μ ∗ l 1785.1 = D*\mu*l 1785.1=D∗μ∗l, 根据流体的动力黏度和滤网厚度可以计算得到黏性阻力系数 D D D，也就是 1 α \frac{1}{\alpha} α1​

3. 用CFD方法获取压降与速度的关系式

建立滤网几何模型的思路

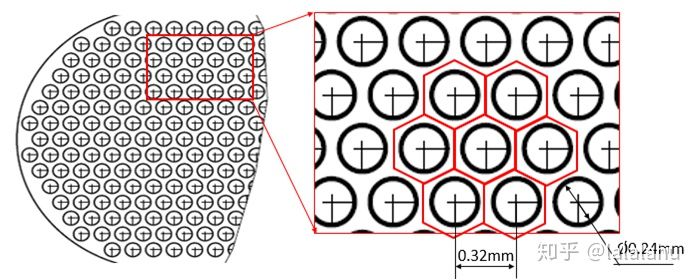
下图是一个滤网的示意图，从图中可以看到小孔的布置方式为六边形布置，即每个小孔和其周围的六个小孔都是等距的，因此可以将整个滤网两侧的流域简化为计算单个小孔，并将周围的流体域取成六棱柱的形状，边长就是两个小孔之间的距离。

这样就可以使用对称边界来将滤网前后的整个流体域简化为六棱柱型的小块流体域。

3D几何和网格

4. fluent设置

其中，relative velocity resistance formulation 勾选表示粘性阻力系数用的是相对速度

alternative formulation 勾选的作用是，当各向异性差异十分明显时（比如10000：1），用以增加收敛性

若流体在某主流方向（如x方向）流通，而其他两方向（y，z方向）不流通，则需要设置其他两个方向（y，z方向）的粘性阻力系数和惯性阻力系数比该主流方向（x方向）的阻力系数大三个数量级

孔隙率为流体所占据的体积分数

thermal model中热平衡指多孔介质基体温度约等于孔间流体温度，非热平衡指基体与孔间流体温度差距较大

relative viscosity（相对粘度）用于计算effective viscosity(有效粘度, which is introduced to account for the effect of the porous medium on the diffusion term in the momentum equations), 计算公式如下
μ e = μ r ∗ μ \mu_e = \mu_r*\mu μe​=μr​∗μ

其中相对粘度 μ r \mu_r μr​可由以下模型计算得到

其中
γ \gamma γ是 porosity of the medium（the volume fraction of fluid within the porous region (that is, the open volume fraction of the medium）

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删