药店路径优化：遗传算法MATLAB实现

1 简介

随着近年来移动机器人应用领域的广泛性以及应用环境的多样性，移动机器人的路径规划成为研究的热门问题，路径规划是引导机器人如何选择最优路线，控制机器人从起点到目标点进行运动，目的是在机器人整个运行过程中，满足某种优化指标如花费时间最少、路径最短或者能量消耗最低。在移动机器人研究领域，通常以罗盘为基础的导向定位、以工业CCD为基础的机器人立体视觉和以环境信息为基础的路径规划是移动机器人研究的三大领域，其中以环境信息为基础的路径规划是前两者的基础。随着智能化的发展，基于搜索式的机器人路径规划算法成为了研究的热门方向，如基于免疫算法的机器人路径规划，基于遗传算法和人工鱼群算法的机器人路径规划。合理的路径规划是移动机器人研究的基础性问题，不仅是研究的核心，更是制约移动式机器人发展的瓶颈血刃。目前，移动机器人在抗震救灾、生命探测、航空航天等领域得到广泛应用，在这些领域的应用前景也是十分辽阔，因此如何求解机器人路径规划问题越来越受到科研工作者的广泛关注与研究。

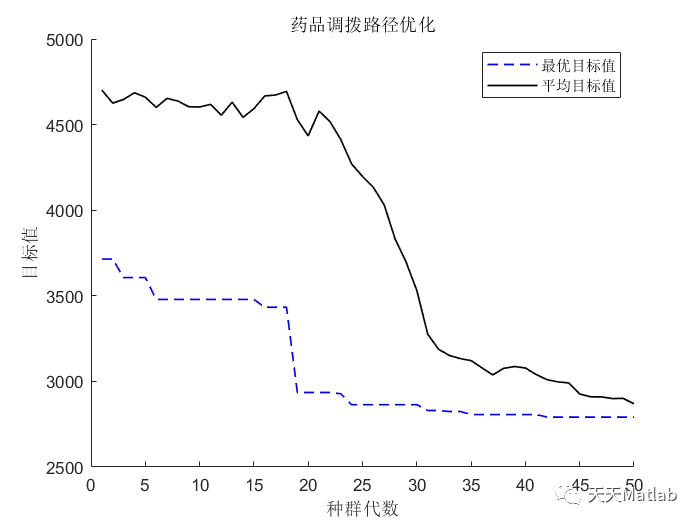
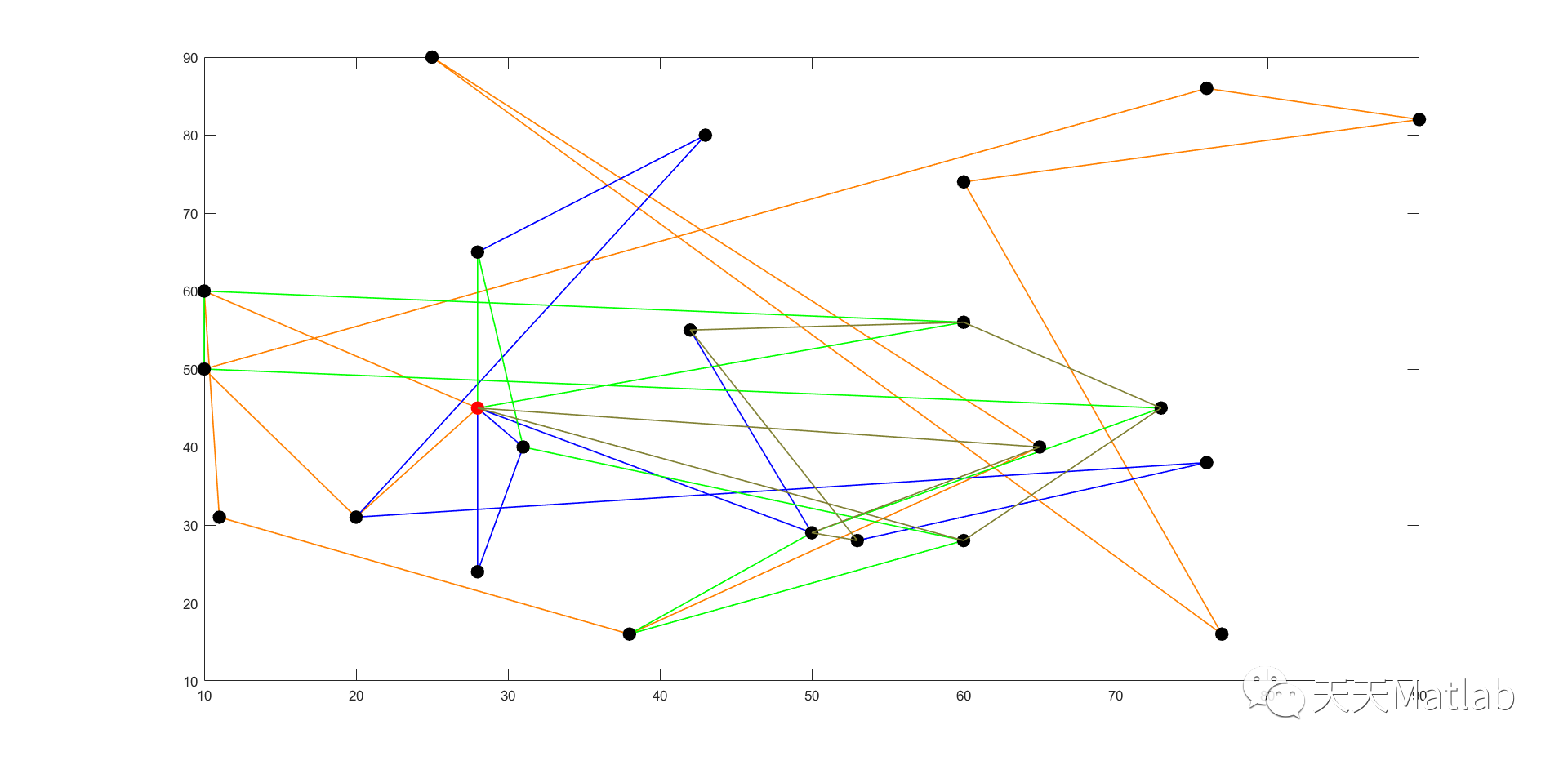
前言在现实生活中,我们经常遇到最短路问题,例如寻找两点之间总长度最短或者费用最低的路径.在运输,物流,设施选址以及人员调度问题中,最短路径是很常见的问题.解决最短路问题的方法有很多,例如迪杰斯特拉算法,福特算法.在这里我们介绍基于遗传算法的药店路径优化问题的解决方案.

2 部分代码

function [f1,f1_1,f1_2,f1_3,shilujing]=fit_all(lujing)%目标函数计算global jiedianglobal maxche%%根据随机产生的路由来确定实际行走lent=size(jiedian,1);jiajie=jiedian(:,4:6);%状态栏chuzuobiao=[28 45];%配送中心zuobiao=[jiedian(:,2:3);chuzuobiao];n=0;%车辆数目f=20;%发车成本c=2;%运输成本v=30;t=0.1;rr=[1 2];for ii=1:floor(lent/2) shilimit(ii,:)=[0,6];endfor ii=floor(lent/2)+1:lent shilimit(ii,:)=[7,12];end %时间窗for ii=1:maxche paixu=lujing(lent*(ii-1)+1:lent*ii);%该车的目标顺序 [luji,jiajie,mimi]=panjue(jiajie,paixu); if size(luji,2)>0 n=n+1; shilujing(n,:)=zeros(1,lent+1); shilujing(n,1:size(luji,2))=luji; endend %%%目标f1_2=0;f1_3=0;f1_1=size(shilujing,1)*f;for ii=1:size(shilujing,1) mop=shilujing(ii,:); iji=find(mop==0); mop=[lent+1,mop(1:iji-1),lent+1]; time=0; for jj=2:size(mop,2) f1_2=f1_2+sqrt((zuobiao(mop(jj),1)-zuobiao(mop(jj-1),1))^2+(zuobiao(mop(jj),2)-zuobiao(mop(jj-1),2))^2)*c; end for jj=2:size(mop,2)-1 time=time+sqrt((zuobiao(mop(jj),1)-zuobiao(mop(jj-1),1))^2+(zuobiao(mop(jj),2)-zuobiao(mop(jj-1),2))^2)/v; f1_3=f1_3+max([shilimit(mop(jj),1)-time,0])*rr(1)+max([time-shilimit(mop(jj),2),0])*rr(2); end endf1=f1_1+f1_2+f1_3;

药店路径优化：遗传算法MATLAB实现

1 简介

2 部分代码

3 仿真结果