1.算法描述
遗传算法的原理
遗传算法GA把问题的解表示成“染色体”,在算法中也即是以二进制编码的串。并且,在执行遗传算法之前,给出一群“染色体”,也即是假设解。然后,把这些假设解置于问题的“环境”中,并按适者生存的原则,从中选择出较适应环境的“染色体”进行复制,再通过交叉,变异过程产生更适应环境的新一代“染色体”群。这样,一代一代地进化,最后就会收敛到最适应环境的一个“染色体”上,它就是问题的最优解。
其主要步骤如下:
1.初始化
选择一个群体,即选择一个串或个体的集合bi,i=1,2,...n。这个初始的群体也就是问题假设解的集合。一般取n=30-160。
通常以随机方法产生串或个体的集合bi,i=1,2,...n。问题的最优解将通过这些初始假设解进化而求出。
2.选择
根据适者生存原则选择下一代的个体。在选择时,以适应度为选择原则。适应度准则体现了适者生存,不适应者淘汰的自然法则。
给出目标函数f,则f(bi)称为个体bi的适应度。以为选中bi为下一代个体的次数。
显然.从式(3—86)可知:
1)适应度较高的个体,繁殖下一代的数目较多。
2)适应度较小的个体,繁殖下一代的数目较少;甚至被淘汰。
这样,就产生了对环境适应能力较强的后代。对于问题求解角度来讲,就是选择出和最优解较接近的中间解。
3.交叉
对于选中用于繁殖下一代的个体,随机地选择两个个体的相同位置,按交叉概率P。在选中的位置实行交换。这个过程反映了随机信息交换;目的在于产生新的基因组合,也即产生新的个体。交叉时,可实行单点交叉或多点交叉。
拟合公式:
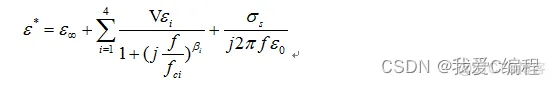
该公式经过化简实部、虚部分离得:

公式化简
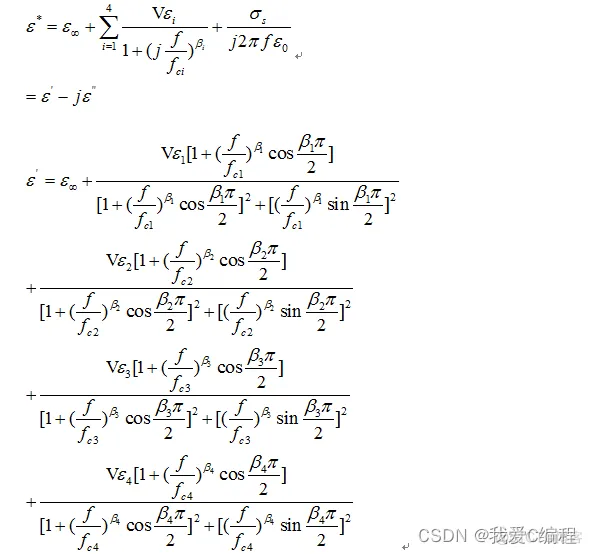

令:
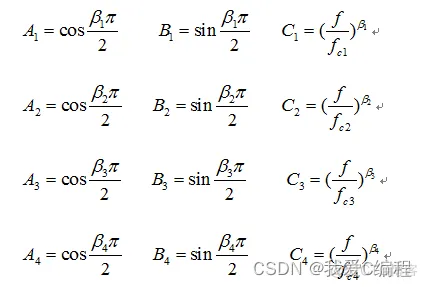
所以:
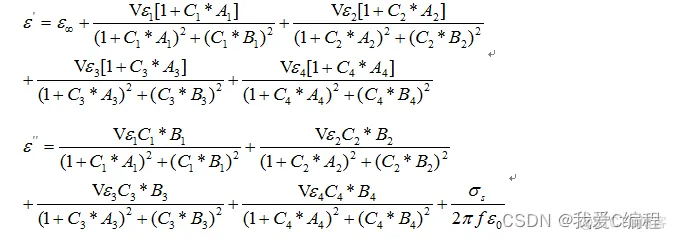
需要拟合的参数有:
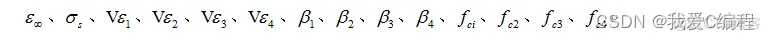
定义GA优化目标函数如下所示:
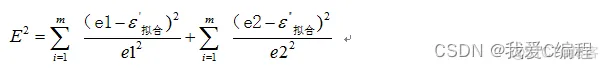
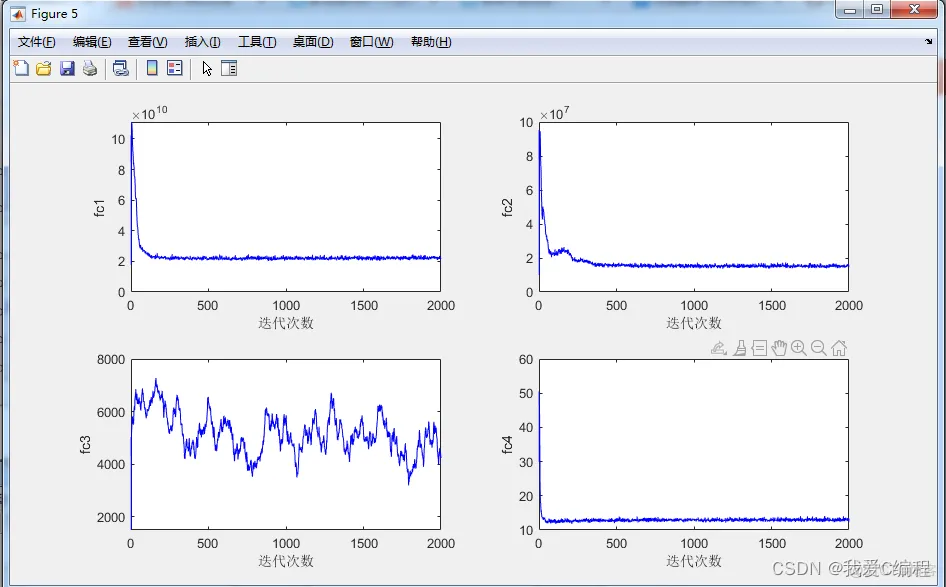
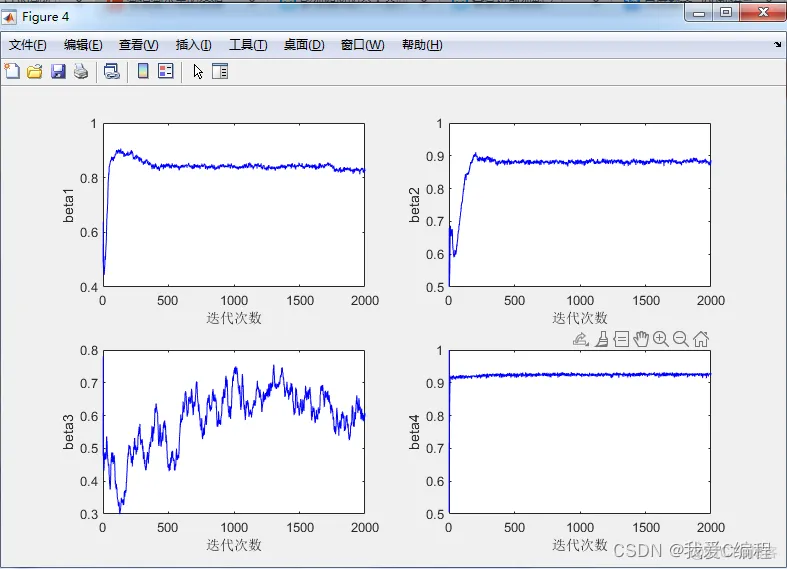
2.仿真效果预览
matlab2022a仿真结果如下:

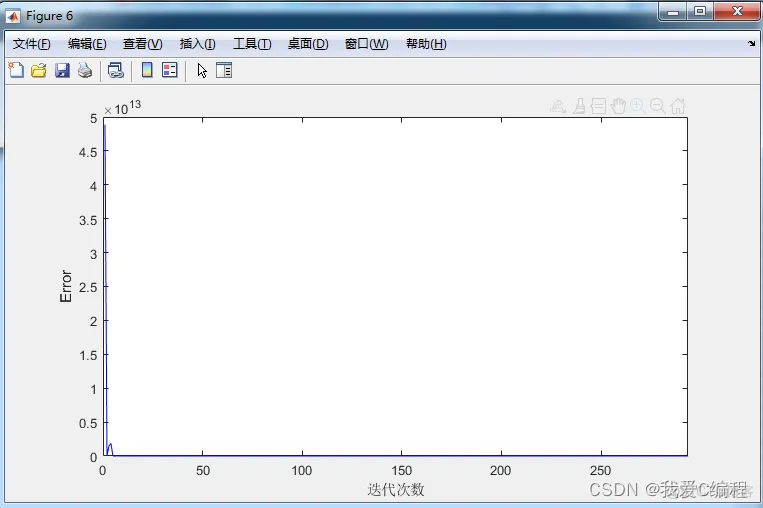
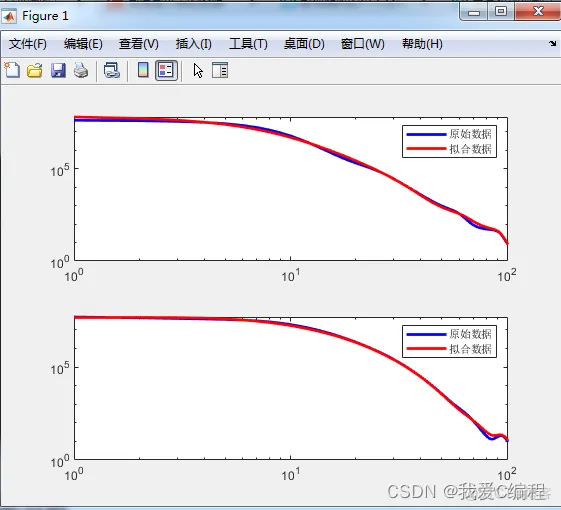
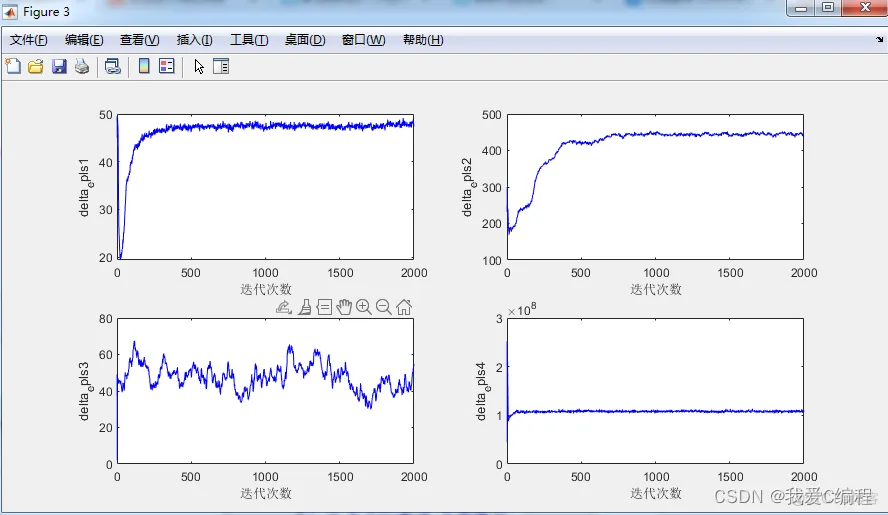
3.MATLAB核心程序
MAXGEN = 2000;
NIND = 400;
Chrom = crtbp(NIND,14*10);
%14个变量的区间
Areas = [0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0 ,0;
10 ,1 ,100 ,500 ,100 ,5e8 ,1 ,1 ,1 ,1 ,2e11,2e8 ,1e4 ,1e2];
FieldD = [rep([10],[1,14]);Areas;rep([0;0;0;0],[1,14])];
epls_inf_NIND = zeros(NIND,1);
deltas_NIND = zeros(NIND,1);
delta_epls1_NIND = zeros(NIND,1);
delta_epls2_NIND = zeros(NIND,1);
delta_epls3_NIND = zeros(NIND,1);
delta_epls4_NIND = zeros(NIND,1);
beta1_NIND = zeros(NIND,1);
beta2_NIND = zeros(NIND,1);
beta3_NIND = zeros(NIND,1);
beta4_NIND = zeros(NIND,1);
fc1_NIND = zeros(NIND,1);
fc2_NIND = zeros(NIND,1);
fc3_NIND = zeros(NIND,1);
fc4_NIND = zeros(NIND,1);
epls_inf = zeros(MAXGEN,1);
deltas = zeros(MAXGEN,1);
delta_epls1 = zeros(MAXGEN,1);
delta_epls2 = zeros(MAXGEN,1);
delta_epls3 = zeros(MAXGEN,1);
delta_epls4 = zeros(MAXGEN,1);
beta1 = zeros(MAXGEN,1);
beta2 = zeros(MAXGEN,1);
beta3 = zeros(MAXGEN,1);
beta4 = zeros(MAXGEN,1);
fc1 = zeros(MAXGEN,1);
fc2 = zeros(MAXGEN,1);
fc3 = zeros(MAXGEN,1);
fc4 = zeros(MAXGEN,1);
Error = zeros(MAXGEN,1);
gen = 0;
for a=1:1:NIND
epls_inf_NIND(a) = epls_inf_0;
deltas_NIND(a) = deltas_0;
delta_epls1_NIND(a) = delta_epls1_0;
delta_epls2_NIND(a) = delta_epls2_0;
delta_epls3_NIND(a) = delta_epls3_0;
delta_epls4_NIND(a) = delta_epls4_0;
beta1_NIND(a) = beta1_0;
beta2_NIND(a) = beta2_0;
beta3_NIND(a) = beta3_0;
beta4_NIND(a) = beta4_0;
fc1_NIND(a) = fc1_0;
fc2_NIND(a) = fc2_0;
fc3_NIND(a) = fc3_0;
fc4_NIND(a) = fc4_0;
%计算对应的目标值
[epls_1,epls_2] = func_obj(f,...
epls_inf_NIND(a),...
deltas_NIND(a),...
delta_epls1_NIND(a),delta_epls2_NIND(a),delta_epls3_NIND(a),delta_epls4_NIND(a),...
beta1_NIND(a),beta2_NIND(a),beta3_NIND(a),beta4_NIND(a),...
fc1_NIND(a),fc2_NIND(a),fc3_NIND(a),fc4_NIND(a));
for m = 1:length(f)
tmps1(m) = ((e1(m)-epls_1(m))^2)/(e1(m)^2);
tmps2(m) = ((e2(m)-epls_2(m))^2)/(e2(m)^2);
end
E = sum(tmps1)+sum(tmps2);
J(a,1) = E;
end
Objv = (J+eps);
gen = 0;
while gen < MAXGEN;
gen
FitnV=ranking(Objv);
Selch=select('sus',Chrom,FitnV);
Selch=recombin('xovsp', Selch,0.9);
Selch=mut( Selch,0.01);
phen1=bs2rv(Selch,FieldD);
for a=1:1:NIND
if gen == 1
epls_inf_NIND(a) = epls_inf_0;
deltas_NIND(a) = deltas_0;
delta_epls1_NIND(a) = delta_epls1_0;
delta_epls2_NIND(a) = delta_epls2_0;
delta_epls3_NIND(a) = delta_epls3_0;
delta_epls4_NIND(a) = delta_epls4_0;
beta1_NIND(a) = beta1_0;
beta2_NIND(a) = beta2_0;
beta3_NIND(a) = beta3_0;
beta4_NIND(a) = beta4_0;
fc1_NIND(a) = fc1_0;
fc2_NIND(a) = fc2_0;
fc3_NIND(a) = fc3_0;
fc4_NIND(a) = fc4_0;
else
epls_inf_NIND(a) = phen1(a,1);
deltas_NIND(a) = phen1(a,2);
delta_epls1_NIND(a) = phen1(a,3);
delta_epls2_NIND(a) = phen1(a,4);
delta_epls3_NIND(a) = phen1(a,5);
delta_epls4_NIND(a) = phen1(a,6);
beta1_NIND(a) = phen1(a,7);
beta2_NIND(a) = phen1(a,8);
beta3_NIND(a) = phen1(a,9);
beta4_NIND(a) = phen1(a,10);
fc1_NIND(a) = phen1(a,11);
fc2_NIND(a) = phen1(a,12);
fc3_NIND(a) = phen1(a,13);
fc4_NIND(a) = phen1(a,14);
end
%计算对应的目标值
[epls_1,epls_2] = func_obj(f,...
epls_inf_NIND(a),...
deltas_NIND(a),...
delta_epls1_NIND(a),delta_epls2_NIND(a),delta_epls3_NIND(a),delta_epls4_NIND(a),...
beta1_NIND(a),beta2_NIND(a),beta3_NIND(a),beta4_NIND(a),...
fc1_NIND(a),fc2_NIND(a),fc3_NIND(a),fc4_NIND(a));
for m = 1:length(f)
tmps1(m) = ((e1(m)-epls_1(m))^2)/(e1(m)^2);
tmps2(m) = ((e2(m)-epls_2(m))^2)/(e2(m)^2);
end
E = sum(tmps1)+sum(tmps2);
JJ(a,1) = E;
end
Objvsel=(JJ+eps);
[Chrom,Objv]=reins(Chrom,Selch,1,1,Objv,Objvsel);
gen=gen+1;
%保存参数收敛过程和误差收敛过程以及函数值拟合结论
epls_inf(gen) = mean(epls_inf_NIND);
deltas(gen) = mean(deltas_NIND);
delta_epls1(gen) = mean(delta_epls1_NIND);
delta_epls2(gen) = mean(delta_epls2_NIND);
delta_epls3(gen) = mean(delta_epls3_NIND);
delta_epls4(gen) = mean(delta_epls4_NIND);
beta1(gen) = mean(beta1_NIND);
beta2(gen) = mean(beta2_NIND);
beta3(gen) = mean(beta3_NIND);
beta4(gen) = mean(beta4_NIND);
fc1(gen) = mean(fc1_NIND);
fc2(gen) = mean(fc2_NIND);
fc3(gen) = mean(fc3_NIND);
fc4(gen) = mean(fc4_NIND);
Error(gen) = mean(JJ);
end
MIN=min(Objv);
for ttt=1:1:size(Objv)
if Objv(ttt)<=MIN
tt=ttt;
break;
end
end
epls_inf_best = epls_inf_NIND(tt);
deltas_best = deltas_NIND(tt);
delta_epls1_best = delta_epls1_NIND(tt);
delta_epls2_best = delta_epls2_NIND(tt);
delta_epls3_best = delta_epls3_NIND(tt);
delta_epls4_best = delta_epls4_NIND(tt);
beta1_best = beta1_NIND(tt);
beta2_best = beta2_NIND(tt);
beta3_best = beta3_NIND(tt);
beta4_best = beta4_NIND(tt);
fc1_best = fc1_NIND(tt);
fc2_best = fc2_NIND(tt);
fc3_best = fc3_NIND(tt);
fc4_best = fc4_NIND(tt);
%计算对应的目标值
[epls_best1,epls_best2] = func_obj(f,...
epls_inf_best,...
deltas_best,...
delta_epls1_best,delta_epls2_best,delta_epls3_best,delta_epls4_best,...
beta1_best,beta2_best,beta3_best,beta4_best,...
fc1_best,fc2_best,fc3_best,fc4_best);
%画图
figure;
subplot(211);
loglog(e1,'b','linewidth',2);
hold on
loglog(epls_best1,'r','linewidth',2);
legend('原始数据','拟合数据');
subplot(212);
loglog(e2,'b','linewidth',2);
hold on
loglog(epls_best2,'r','linewidth',2);
legend('原始数据','拟合数据');
02_016m
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删