Matlab进阶学习：遗传算法实战指南

优化问题是相当大一部分科研问题中的主要问题之一，当建立起一个数模模型后如何找到这个模型的最优解或者较优解。常用的方法包括

• 穷举法（理论可以找到最优解，就是太慢了，一般没人用这种）
• 解析式推导最优解（大部分情况下推不出来或者解析式很复杂无法应用）
• 凸优化算法（很多情况下可以推，但是同样有更多情况下问题非凸）
• 非凸问题转换为凸问题后，使用凸优化算法
• 智能优化算法（可以适用于各类优化问题，包括凸和非凸的，良好设计的情况下可以取得较好的效果）

这一章首先介绍智能优化算法中的遗传算法。

遗传算法

简介：遗传算法（Genetic Algorithm）是一种通过模拟自然进化过程搜索最优解的方法，该算法在智能优化算法里属于全局优化算法，比较适合于最优解对个别基因变化不敏感的情况。

常用或者说常见的遗传算法的优化流程如下所示：

1. 产生初始种群（可以是全随机也可以是固定模式）
2. 种群通过变异、交叉等方式产生新的个体（变异、交叉的方式并不固定）
3. 计算新种群中个体的环境适应度（适应度函数的很重要）
4. 种群根据环境适应度进行自然选择淘汰个体，维护种群规模（淘汰方式可选）
5. 重复步骤2-5直至到达停止条件。

在上述描述的步骤中（其中名词描述不知道的仔细搜索），进行遗传算法优化时有几点要素需要注意或者说需要设计

• 编码方式，即问题的解与个体基因的对应关系
• 初始种群的产生方式
• 变异和交叉的方式
• 不满足约束的解的处理方式
• 适应度函数

以上列出五点是将你的问题应用到遗传算法中首要解决的问题，以上5点设计好了你的遗传算法才可能帮你找到合适的最优解。下面我将一一展开介绍

一、编码设计

编码设计是解决问题的解与个体基因的对应关系的关键，你的问题的解本来是一种抽象的表示，要将遗传算法应用其中必须构建一个转换函数f可以将编码x转换为你要的实际解y。

此举将原来的优化问题，ybest=argmax（g(y)）转换为xbest=argmax(g(f(x))),ybest=f(xbest)

常用的编码方式有二进制编码、整数编码、浮点编码三种，在设计和选用编码方式时必须注意以下几点

• 此编码方式是否会导致很多的无效解。无效解的存在对于遗传算法是致命的，这就相当于你要优化目标函数中存在大量深坑，如果后续的处理中无法很好的调整无效解，此处必须考虑设计一种可以避免无效解的编码方式。
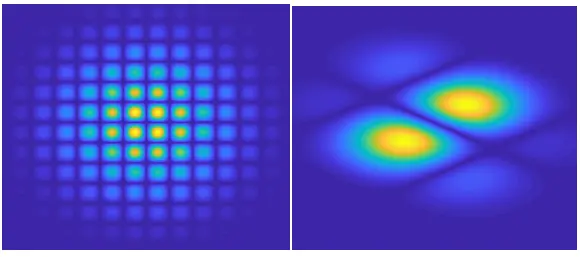
• 此编码得到的实际的目标函数g(f(x))是否适用于遗传算法优化，遗传算法是全局优化算法这类算法有一种很明显的特性就是不适合优化有大量局部突变特性的优化情况。如下图所示，右图更适合遗传算法，左图更适合鱼群算法这类局部优化算法。

二、初始种群的产生

初始种群本身一般是随机生成的，他的随机性保证了整体种群的基因类型的丰富性，因此初始群通常是在解空间内随机生成种群。

常用的生成方式有两种

• 编码每个值独立完全随机生成。
• 根据解的规则进行随机生成。

生成过程需要注意啥呢，还是无效解的问题，部分情况解的规则很复杂，只能完全随机生成，存在大量的无效解，需要解决。

三、变异和交叉方式

变异和交叉时遗传算法产生新解的方式，是后续遗传算法优化的关键因素之一。

交叉：出了一部分可以用作交叉的父母个体，而染色体交叉操作，就是指在这些父母个体中，选择两个进行相互交配，将他们的染色体按照某种方式相互交换部分基因，形成两个新的个体的过程。（全局调整）

变异： 在交叉操作过后形成的新个体，有一定的概率会发生基因变异（局部调整）。

常见的交叉方式：

• Partial-Mapped Crossover (PMX)，随机选择基因段的起止位置，交换这两组基因的位置，做冲突检测，根据交换的两组基因建立一个映射关系。
• Order Crossover (OX)，随机选择基因段的起止位置，保留选取的基因，其他基因按照顺序从另一组基因中获取。
• Position-based Crossover (PBX)， 随机选择基因几个基因保留，其他基因按照顺序从另一组基因中获取。  
• 叠加Crossover，  随机选择基因段的起止位置，两组基因按不同比例进行叠加，产生新解（主要适用于整数或者浮点编码）。

常见的变异算子： 

• 基本位变异：对个体编码串中以变异概率、随机指定的某一位或某几位仅因座上的值做变异运算。
• 均匀变异：分别用符合某一范围内均匀分布的随机数，以某一较小的概率来替换个体编码串中各个基因座上的原有基因值。
• 边界变异：随机的取基因座上的两个对应边界基因值之一去替代原有基因值。特别适用于最优点位于或接近于可行解的边界时的一类问题。
• 非均匀变异：对原有的基因值做一随机扰动，以扰动后的结果作为变异后的新基因值。对每个基因座都以相同的概率进行变异运算之后，相当于整个解向量在解空间中作了一次轻微的变动。
• 高斯近似变异：进行变异操作时用符号均值为Ｐ的平均值，方差为P**2的正态分布的一个随机数来替换原有的基因值。

四、不满足约束的解的处理方式

上述新解产生的过程，没有完全考虑到约束问题，实际情况中如果任由不合适的解保存在种群中，会导致整体的处理效率都很低下，更遑论找到最优解了。

常用的解决方法：

• 在自然选择中抛弃这些不满足规则的解
• 将不满足约束的解按照规则调整为满足约束的解
• 设计惩罚函数使得自然选择过程中选中不满足约束的解概率降低

有效的规避约束问题还是要靠编码，这里只能说可以避免这种问题的出现。

五、适应度函数设计

适应度的含义就是字面意思，这个个体是否可以适应环境也即是否满足优化目标指标。因为后续需要根据适应度函数进行自然选择，因此适应度函数和你的目标函数并不需要完全一样。

常用的适应度函数设计有哪些呢？我常用的方式有以下几种

• 直接用目标函数或其倒数，简单但是缺点是可能导致种群多样性过大或者过小
• 目标函数套上其他函数f(x)，改变适应度的分布情况。
• 种群根据整体目标函数值的情况，进行归一化等操作，保证每次适应度分布情况。

注意事项：

遗传算法的优化过程中种群基因的多样性是保障避免陷入局部最优解的重要因素，如果目标函数优化结果过早收敛很可能就是因为种群的多样性不足。

为了保证种群的多样性，其中编码、适应度函数设计尤为重要。

下一期预告《Matlab从入门到精通（2）——遗传算法案例--TSP问题》