Matlab优化算法：遗传、粒子群与差分进化求解

1. Schwefel's函数

Schwefel's函数是一个典型的欺骗问题，有1个全局极小值点，距离另一个局部最优点很远，因此如果陷入局部最优就很难跳出。Schwefel’s函数的表达式为：

2. 问题求解

笔者将采用遗传算法、粒子群算法和差分进化算法对Schwefel’s问题分别进行求解，同时，对三种算法的结果进行对比分析。

这里，首先定义一下问题：

function z=test_func(in) z = zeros(size(in,1),1); for i=1:size(in,1)    x = in(i,:);    for j=1:size(in,2)        temp = x(j) * sin(sqrt(abs(x(j))));        z(i,1) = z(i,1) + temp;    endendz = -z;

2.1 遗传算法

Matlab中自带了遗传算法的工具箱，通过help ga可以查看相关的帮助文档。

This MATLAB function finds a local unconstrained minimum, x, to the objective    function, fitnessfcn. [x,fval] = ga(fitnessfcn,nvars,A,b,Aeq,beq,LB,UB)

图形化界面操作如下：

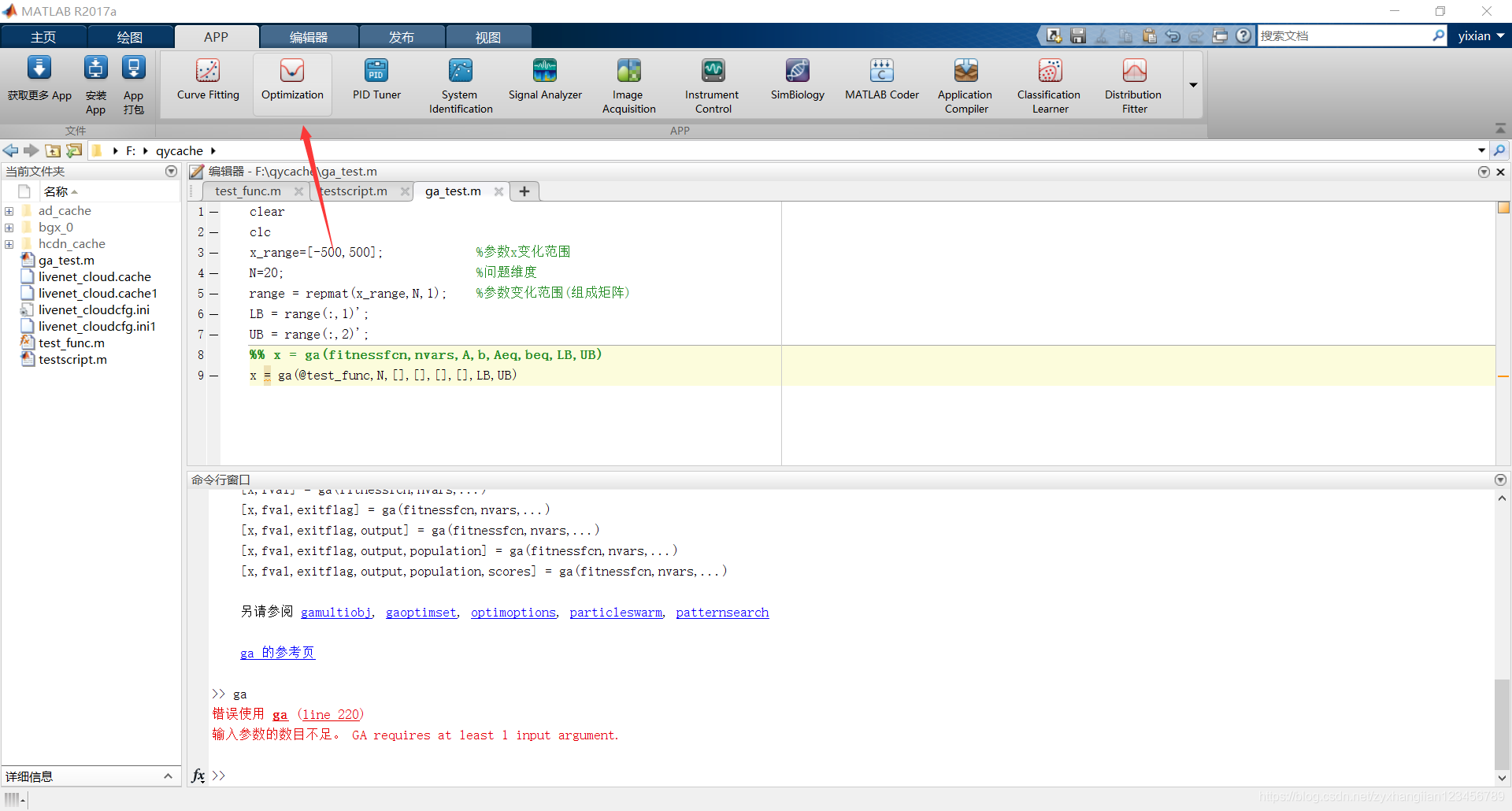
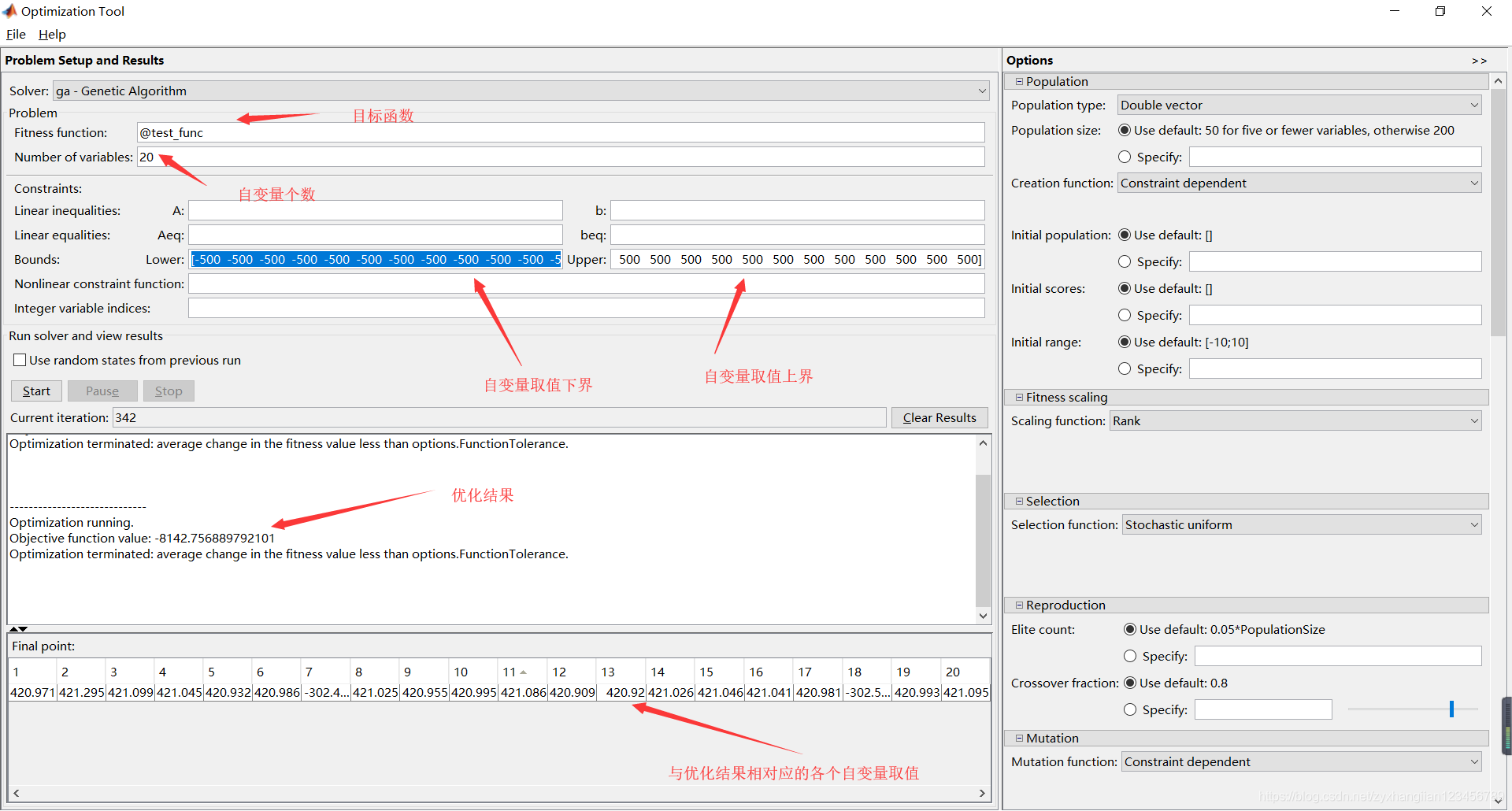
代码求解如下：

clearclcx_range=[-500,500];            N=20;                           range = repmat(x_range,N,1);   LB = range(:,1)';UB = range(:,2)';%% x = ga(fitnessfcn,nvars,A,b,Aeq,beq,LB,UB)[x,fval] = ga(@test_func,N,[],[],[],[],LB,UB)

结果：

Optimization terminated: average change in the fitness value less than options.FunctionTolerance. x = 420.9547  421.0920  420.9799  420.9657  420.9217  421.0547  420.9840  420.9485  421.0406  421.0243 -302.3978  421.0425  421.0161  421.0313  420.9623  420.9485  421.1032  421.0249  420.9671  420.9783 fval =  -8.2612e+03

2.2 粒子群算法

笔者这里设置最大迭代次数为1000，种群规模问250时，利用粒子群算法工具箱求解代码：

clearclcx_range=[-500,500];             %参数x变化范围N=20;                           %问题维度range = repmat(x_range,N,1);    %参数变化范围(组成矩阵)Max_V = 0.1*(range(:,2)-range(:,1));  %最大速度取变化范围的10%~20%Pdef = [100 1000 250 2 2 0.9 0.4 1500 1e-25 250 NaN 0 0];%% Functname, D, mv, Varrange, minmax, and psoparamspso_Trelea_vectorized('test_func',N,Max_V,range,0,Pdef)  %调用PSO核心模块

运行结果：

2.3 差分进化算法

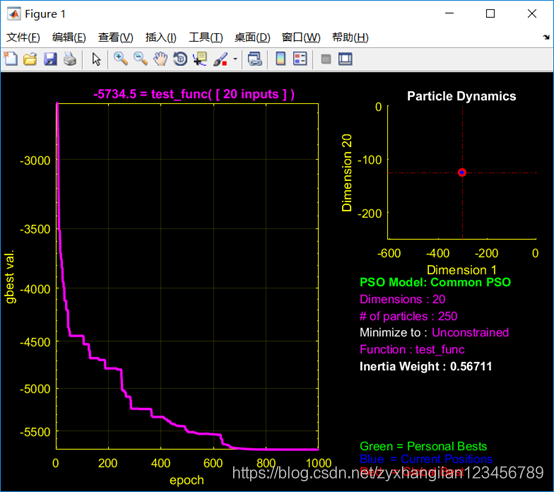
笔者借助于Differential Evolution (DE)工具箱，进行了问题求解，具体工具箱代码可以到：https://ww2.mathworks.cn/matlabcentral/fileexchange/52897-differential-evolution-de?s_tid=srchtitle 下载。

如下是差分进化算法求解Schwefel's问题的matlab程序：

%% Problem DefinitionCostFunction=@(x) test_func(x);    % Cost FunctionnVar=20;            % Number of Decision VariablesVarSize=[1 nVar];   % Decision Variables Matrix SizeVarMin=-500;          % Lower Bound of Decision VariablesVarMax= 500;          % Upper Bound of Decision Variables %% DE ParametersMaxIt=1000;      % Maximum Number of IterationsnPop=50;        % Population Sizebeta_min=0.2;   % Lower Bound of Scaling Factorbeta_max=0.8;   % Upper Bound of Scaling FactorpCR=0.2;        % Crossover Probability %% Initializationempty_individual.Position=[];empty_individual.Cost=[];BestSol.Cost=inf;pop=repmat(empty_individual,nPop,1);for i=1:nPop    pop(i).Position=unifrnd(VarMin,VarMax,VarSize);    pop(i).Cost=CostFunction(pop(i).Position);    if pop(i).Cost<BestSol.Cost        BestSol=pop(i);    endend BestCost=zeros(MaxIt,1); %% DE Main Loopfor it=1:MaxIt    for i=1:nPop        x=pop(i).Position;        A=randperm(nPop);        A(A==i)=[];        a=A(1);        b=A(2);        c=A(3);         % Mutation        %beta=unifrnd(beta_min,beta_max);        beta=unifrnd(beta_min,beta_max,VarSize);        y=pop(a).Position+beta.*(pop(b).Position-pop(c).Position);        y = max(y, VarMin);        y = min(y, VarMax);                 % Crossover        z=zeros(size(x));        j0=randi([1 numel(x)]);        for j=1:numel(x)            if j==j0 || rand<=pCR                z(j)=y(j);            else                z(j)=x(j);            end        end         NewSol.Position=z;        NewSol.Cost=CostFunction(NewSol.Position);         if NewSol.Cost<pop(i).Cost            pop(i)=NewSol;            if pop(i).Cost<BestSol.Cost               BestSol=pop(i);            end        end    end     % Update Best Cost    BestCost(it)=BestSol.Cost;     % Show Iteration Information    disp(['Iteration ' num2str(it) ': Best Cost = ' num2str(BestCost(it))]);end %% Show Resultsfigure;%plot(BestCost);semilogy(BestCost, 'LineWidth', 2);xlabel('Iteration');ylabel('Best Cost');grid on;

结果：

Iteration 1000: Best Cost = -8379.6577

从结果中可以看出，遗传算法和差分进化算法能够较好地求解该多欺骗问题，其中，差分进化算法表现最优，遗传算法次之，而粒子群算法容易陷入局部最优解。以上实验仅为个人的实验结果，不能作为衡量不同算法优劣的标准。

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删