GA遗传优化flog任务调度：MATLAB仿真实践

1.算法仿真效果

matlab2022a仿真结果如下：

2.算法涉及理论知识概要

遗传算法GA把问题的解表示成“染色体”，在算法中也即是以二进制编码的串。并且，在执行遗传算法之前，给出一群“染色体”，也即是假设解。然后，把这些假设解置于问题的“环境”中，并按适者生存的原则，从中选择出较适应环境的“染色体”进行复制，再通过交叉，变异过程产生更适应环境的新一代“染色体”群。这样，一代一代地进化，最后就会收敛到最适应环境的一个“染色体”上，它就是问题的最优解。

登录后复制

其主要步骤如下：

2.1．初始化

登录后复制

选择一个群体，即选择一个串或个体的集合bi，i=1，2，...n。这个初始的群体也就是问题假设解的集合。一般取n＝30-160。通常以随机方法产生串或个体的集合bi,i＝1，2，...n。问题的最优解将通过这些初始假设解进化而求出。

2.2．选择

登录后复制

根据适者生存原则选择下一代的个体。在选择时，以适应度为选择原则。适应度准则体现了适者生存，不适应者淘汰的自然法则

给出目标函数f，则f(bi)称为个体bi的适应度。以为选中bi为下一代个体的次数。显然．从式(3—86)可知：

1)适应度较高的个体，繁殖下一代的数目较多。

2)适应度较小的个体，繁殖下一代的数目较少；甚至被淘汰。

这样，就产生了对环境适应能力较强的后代。对于问题求解角度来讲，就是选择出和最优解较接近的中间解。

3.3．交叉

登录后复制

对于选中用于繁殖下一代的个体，随机地选择两个个体的相同位置，按交叉概率P。在选中的位置实行交换。这个过程反映了随机信息交换；目的在于产生新的基因组合，也即产生新的个体。交叉时，可实行单点交叉或多点交叉。

3.MATLAB核心程序

登录后复制

MaxIt = 60;	% 最大迭代次数
nPop  = 50;	% 人口规模
pc    = 0.8;                 % 交叉百分比
nc    = 2*round(pc*nPop/2);  % 子代数量（也包括Parnets）
pm    = 0.4;                 % 突变百分比
nm    = round(pm*nPop);      % 突变体数量
mu    = 0.05;                % 突变率
UseRandomSelection =true; 
pause(0.01); 
Best_Orchestration=[];
%初始化
for step=1:1
    S=CreatTask(S,1);
    for i=1:length(S)
        Tasks(i)=S{i}.Tasks;
    end
    empty_individual.Position = [];
    empty_individual.Cost = [];
    pop = repmat(empty_individual, nPop, 1);
    for i = 1:nPop
        %初始化位置
        pop(i).Position = randerr(SensorNum,FogNum)';
        %评价
        pop(i).Cost = NetworkModel(pop(i).Position,S,F,Tasks); 
    end
    %排序填充
    Costs = [pop.Cost];
    [Costs, SortOrder] = sort(Costs,'descend');
    pop = pop(SortOrder);
    %存储最佳解决方案
    BestSol = pop(1);
    %保持最佳成本值的阵列
    BestCost = zeros(MaxIt, 1);
    %成本
    WorstCost = pop(end).Cost;
    for it = 1:MaxIt
        it
        % Crossover
        popc = repmat(empty_individual, nc/2, 2);
        for k = 1:nc/2
            i1 = randi([1 nPop]);
            i2 = randi([1 nPop]);
            % Select
            p1 = pop(i1);
            p2 = pop(i2);
            % Perform Crossover
            [popc(k, 1).Position, popc(k, 2).Position] =MyCrossOver(p1.Position, p2.Position);
            % Evaluate Offsprings
            popc(k, 1).Cost = NetworkModel(popc(k,1).Position,S,F);
            popc(k, 2).Cost = NetworkModel(popc(k,2).Position,S,F);
        end
        popc = popc(:);
...........................................................................
        % Create Merged Population
        pop = [pop
            popc
            popm]; %#ok
        % Sort Population
        Costs = [pop.Cost];
        [Costs, SortOrder] = sort(Costs,'descend');
        pop = pop(SortOrder);
        % Update Worst Cost
        WorstCost = max(WorstCost, pop(end).Cost);
        % Truncation
        pop = pop(1:nPop);
        Costs = Costs(1:nPop);
        BestSol = pop(1);
        BestCost(it) = BestSol.Cost;
    end
    %Results
    [cost_func,total_cost(step),make_span(step),total_distance(step)]=NetworkModel(BestSol.Position,S,F)
    [rx,cx]                   = size(BestSol.Position);
    Best_Nodes_For_Tasks      = ChromosomeEncoding(BestSol.Position,rx,cx);
    Best_Orchestration(step,:)= Best_Nodes_For_Tasks;
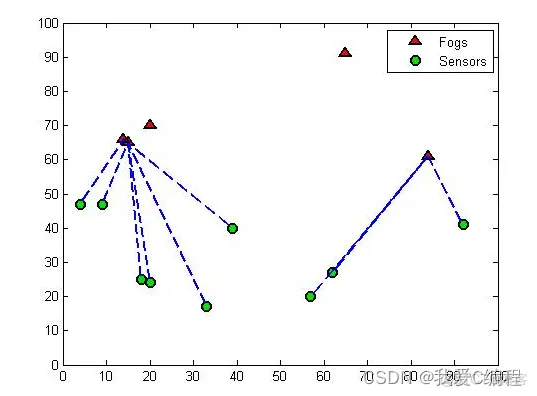
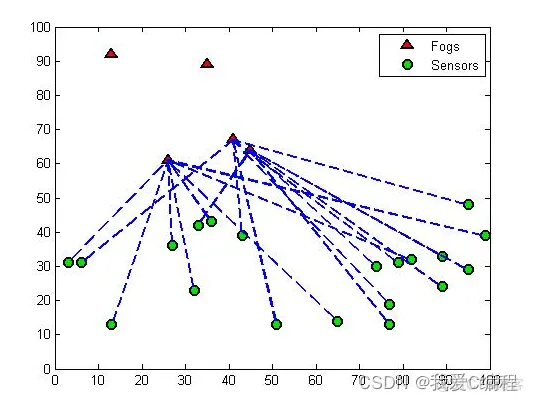
    PlotFogCluser(F,S,Best_Nodes_For_Tasks,step);
    
    figure;
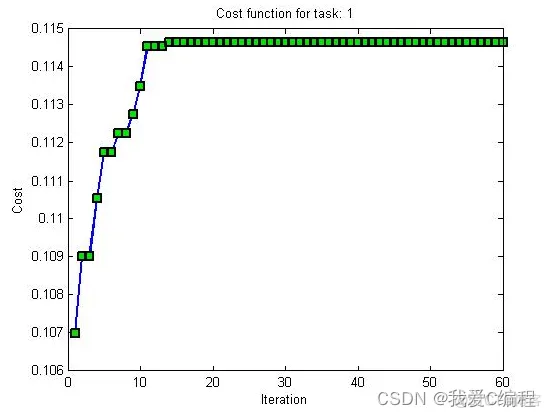
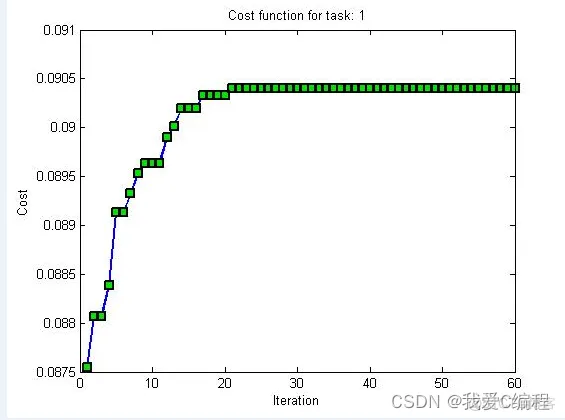
    plot(BestCost,'-bs',...
    'LineWidth',2,...
    'MarkerSize',8,...
    'MarkerEdgeColor','k',...
    'MarkerFaceColor',[0.0,0.9,0.0]);
    xlabel('Iteration');
    ylabel('Cost');
    title(['Cost function for task: ',num2str(step)])
end
A327

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删