MSOPSO多策略粒子群算法目标优化MATLAB仿真探索

1.算法描述

粒子群优化算法(particle swarm optimization，PSO)是一种源于对鸟群捕食行为的研究而发明的进化计算技术，最先由Eberhart 博士和Kennedy 博士提出，其主要想法是：将每个优化问题的解看作是搜索空间中的一个没有体积的粒子，在搜索空间中以一定的速度飞行，速度的大小与方向根据它本身和同伴的飞行经验来动态调整。

登录后复制

粒子Xi 在第t 次进行迭代的速度与位置运算公式为：

登录后复制

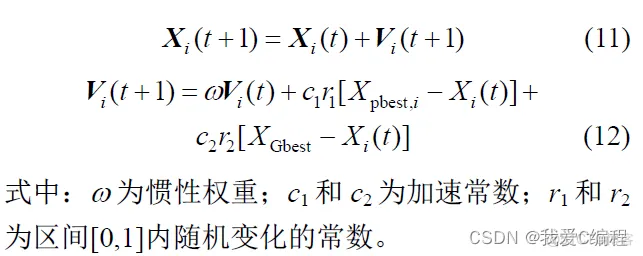
当进化过程中产生新个体X 时，同时对该个体的反向位置Xi 进行考察，综合比较产生一个更优的个体。这样，个体Xi与最优位置之间的距离就会缩小，从而提高算法的效率。

在粒子群算法优化过程的初期，大数值的权重系数可以增强全局搜索能力；在优化过程的后期，小数值的迭代权重将有利于局部搜索；而常数权重无法调节这两方面的搜索能力，所以本文通过引入随时间变化的权重系数来平衡全局搜索和局部搜索能力。

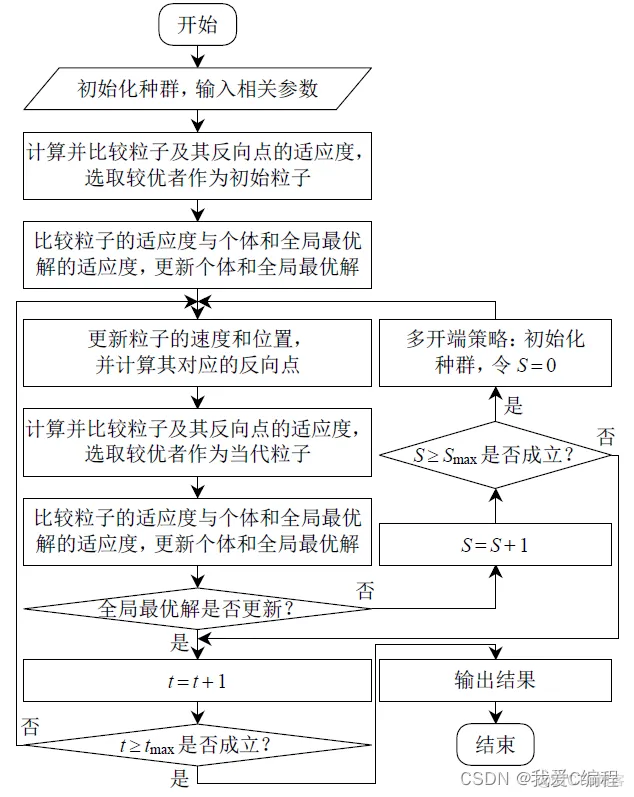
 MSOPSO 算法流程图：

2.matlab算法仿真效果

matlab2022a仿真结果如下：

3.MATLAB核心程序

登录后复制

y_best    = zeros(1,Pop);
 
Smax      = 100;
S         = 0;
%粒子初始化
for i=1:Pop
    %N
    x1(1,i)         = rand(1)*(max1-min1)+min1;
    x_best1(1,i)    = rand(1)*(max1-min1)+min1;
    %I
    y1(1,i)         = rand(1)*(max2-min2)+min2;
    y_best1(1,i)    = rand(1)*(max2-min2)+min2;
 
    %反向学习初始化
    %N
    x_(1,i)        = (max1+min1)-x(1,i);
    x_best_(1,i)   = (max1+min1)-x_best(1,i);
    %I
    y_(1,i)        = (max2+min2)-y(1,i);
    y_best_(1,i)   = (max2+min2)-y_best(1,i);
    
    
    [BsJ1,x(1,i),y(1,i)] = func_fitness(x1(1,i),y1(1,i)); 
    [BsJ2,x(1,i),y(1,i)] = func_fitness(x_(1,i),y_(1,i));    
    
    if BsJ1 < BsJ2
        %N
        x(1,i)         = x1(1,i);
        x_best(1,i)    = x_best1(1,i);
        %I
        y(1,i)         = y1(1,i);
        y_best(1,i)    = y_best1(1,i);
        BsJi(i)        = BsJ1;
    else
        %N
        x(1,i)         = x_(1,i);
        x_best(1,i)    = x_best_(1,i);
        %I
        y(1,i)         = y_(1,i);
        y_best(1,i)    = y_best_(1,i);
        BsJi(i)        = BsJ2;
    end
 
    va(1,i)   =(vmax-vmin)*rand(1)+vmin;
    vb(1,i)   =(vmax-vmin)*rand(1)+vmin;
end
[minJi,index]= min(BsJi);
 
Tx_best    = 500;
Ty_best    = 500;
for t=1:tmax
    t
    time(t) = t;
    w       = wmax-t*(wmax-wmin)/tmax;
    c2      = c2max-t*(c2max-c2min)/tmax;
    for i=1:Pop
        if t > 1
            %N
            x(1,i)         = x_(1,i);
            x_best(1,i)    = x_best_(1,i);
            %I
            y(1,i)         = y_(1,i);
            y_best(1,i)    = y_best_(1,i);
        end
        %N
        %速度1设置
        va(1,i) = w*va(1,i) + c1*rand(1)*(x_best(1,i)-x(1,i)) + c2*rand(1)*(Tx_best-x(1,i));
        %更新
        x(1,i)  = x(1,i) + va(1,i);
        %变量1的限制
        if x(1,i) >= max1
           x(1,i) = max1;
        end
        if x(1,i) <= min1
           x(1,i) = min1;
        end                             
 
        %I
        %速度2设置
        vb(1,i) = w*vb(1,i) + c1*rand(1)*(y_best(1,i)-y(1,i)) + c2*rand(1)*(Ty_best-y(1,i));
        %更新
        y(1,i)  = y(1,i) + vb(1,i);
        %变量2的限制
        if y(1,i) >= max2
           y(1,i) = max2;
        end
        if y(1,i) <= min2
           y(1,i) = min2;
        end                           
 
        [BsJ,x(1,i),y(1,i)] = func_fitness(x(1,i),y(1,i));  
        
        if BsJ<BsJi(i)
           BsJi(i)        = BsJ;
           x_best(1,i)    = x(1,i);
           y_best(1,i)    = y(1,i);
        end
        if BsJi(i)<minJi
           minJi      = BsJi(i);
           Tx_best    = x(1,i);
           Ty_best    = y(1,i);
        end
        %反向
        %反向
        %反向学习
        %N
        x_(1,i)         = (max1+min1)-x(1,i);
        x_best_(1,i)    = (max1+min1)-x_best(1,i);
        %I
        y_(1,i)         = (max2+min2)-y(1,i);
        y_best_(1,i)    = (max2+min2)-y_best(1,i);
        
        %计算反向点和当前点的适应度
        [BsJa,xa(1,i),ya(1,i)] = func_fitness(x(1,i),y(1,i));
        [BsJb,xb(1,i),yb(1,i)] = func_fitness(x_(1,i),y_(1,i));
        
        %选择较优点
        if BsJa <= BsJb
            x(1,i)         = x(1,i);
            x_best(1,i)    = x_best(1,i);
            %I
            y(1,i)         = y(1,i);
            y_best(1,i)    = y_best(1,i);
        else
            x(1,i)         = x_(1,i);
            x_best(1,i)    = x_best_(1,i);
            %I
            y(1,i)         = y_(1,i);
            y_best(1,i)    = y_best_(1,i);
        end
        [BsJ,x(1,i),y(1,i)] = func_fitness(x(1,i),y(1,i));
 
        
        if BsJ<BsJi(i)
           BsJi(i)        = BsJ;
           x_best(1,i)    = x(1,i);
           y_best(1,i)    = y(1,i);
        end
        if BsJi(i)<minJi
           minJi      = BsJi(i);
           Tx_best    = x(1,i);
           Ty_best    = y(1,i);
        end 
    end
    %判断全局最优解是否有更新
    Jibest(t) = minJi;
    
    if t > 1
       if abs(Jibest(t) - Jibest(t-1)) < 0.0001%认为没有更新
          S = S + 1; 
          if S >= Smax%多开端策略，种群重新初始化，用于下一次迭代使用
             for i=1:Pop
                %N
                x(1,i)         = rand(1)*(max1-min1)+min1;
                x_best(1,i)    = rand(1)*(max1-min1)+min1;
                %I
                y(1,i)         = rand(1)*(max2-min2)+min2;
                y_best(1,i)    = rand(1)*(max2-min2)+min2;
 
                %反向学习初始化
                %N
                x_(1,i)        = (max1+min1)-x(1,i);
                x_best_(1,i)   = (max1+min1)-x_best(1,i);
                %I
                y_(1,i)        = (max2+min2)-y(1,i);
                y_best_(1,i)   = (max2+min2)-y_best(1,i);
             end
          S=0;   
          end
       end
    end
 
end
02_042m

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删