2.本算法理论知识
NSGA-II适合应用于复杂的、多目标优化问题。是K-Deb教授于2002在论文:A Fast and Elitist Multiobjective Genetic Algorithm:NSGA-II,中提出。在论文中提出的NSGA-II解决了NSGA的主要缺陷,实现快速、准确的搜索性能。NSGA的非支配排序的时间复杂度为O(MN3)O(MN3),在种群规模N较大时排序的速度会很慢。NSGA-II使用带精英策略的快速非支配排序,时间复杂度为O(M(2N)2)O(M(2N)2),排序速度有大幅的提升。而且使用了精英策略,保证了找到的最优解不会被抛弃,提高了搜索性能。另一方面NSGA使用共享函数来使解分布均匀,该函数依赖于共享参数σshareσshare的选择,而且共享函数的复杂度高达O(N2)O(N2)。NSGA-II从新定义了拥挤距离来代替共享参数。其算法流程如下:

3.核心代码
clc;clear;close all;warning off;global Len;global WindDataPV;global SolarDataPVR;global LoadDataPV;%数据长度Len = 876;[WindDataPV,SolarDataPVR,LoadDataPV] = ReadLocalClimaticData(Len);%初始化参数popnum = 120;gen = 100;%变量取值范围xmin = 0;xmax = 1;%目标函数个数m = 3; %决策变量数目n = 30;%交叉变异参数hc = 15;hm = 15;%产生初始种群initpop = rand(popnum,n)*(xmax-xmin)+xmin;init_value_pop = value_objective(initpop,m,n);%画图显示初始图figure plot(init_value_pop(:,n+1),init_value_pop(:,n+m),'B+')pause(.1)%非支配排序和聚集距离计算[non_dominant_sort_pop,rankinfo] = non_dominant_sort(init_value_pop,m,n);ns_dc_pop = crowding_distance(non_dominant_sort_pop,m,n,rankinfo);%选择,交叉,变异产生下一个子代%选择进行交叉变异的个数poolsize = round(popnum/2);%选择锦标赛的元度toursize = 2;select_pop = selection(ns_dc_pop,poolsize,toursize,m,n);%存储交叉变异相关参数hc = 20;hm = 20;offspring = genetic_operate(select_pop,m,n,hc,hm,xmax,xmin);%循环开始t=1;while t<=gen t %合并种群(2N),进入循环 combine_pop(1:popnum,1:m+n+2) = ns_dc_pop; [xsize,ysize] = size(offspring); combine_pop(popnum+1:popnum+xsize,1:m+n+2) = offspring; %重新进行非支配排序和聚焦距离计算 [gen_non_dominant_pop,rankinfo] = non_dominant_sort(combine_pop,m,n); nsdc_pop = crowding_distance(gen_non_dominant_pop,m,n,rankinfo); %选择下一代的产生(然后用于交叉变异) ns_dc_pop = generate_offsprings(nsdc_pop,m,n,popnum); %显示下一代的情况N_decision_var if m==2 plot(ns_dc_pop(:,n+1),ns_dc_pop(:,n+2),'r*') elseif m==3 plot3(ns_dc_pop(:,n+1),ns_dc_pop(:,n+2),ns_dc_pop(:,n+3),'kd') xlabel('Function 1'); ylabel('Function 2'); zlabel('Function 3'); view([44,34]); end grid on; text(0,0,0,['第 ',int2str(t),' 代']); pause(0.1) %选择,交叉,变异产生下一个子代 poolsize = round(popnum/2);%选择进行交叉变异的个数 toursize = 2;%选择锦标赛的元度 select_pop = selection(ns_dc_pop,poolsize,toursize,m,n); hc = 20;%存储交叉变异相关参数 hm = 20; offspring = genetic_operate(select_pop,m,n,hc,hm,xmax,xmin); t = t+1;end%显示标题xlabel('经济效益');ylabel('缺失率%');zlabel('排污水平');view([44,34]);1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.36.37.38.39.40.41.42.43.44.45.46.47.48.49.50.51.52.53.54.55.56.57.58.59.60.61.62.63.64.65.66.67.68.69.70.71.72.73.74.75.76.77.78.79.80.81.82.83.84.85.86.87.88.89.90.91.92.
4.操作步骤与仿真结论
运行NSGA2.m,得到如下仿真结果:
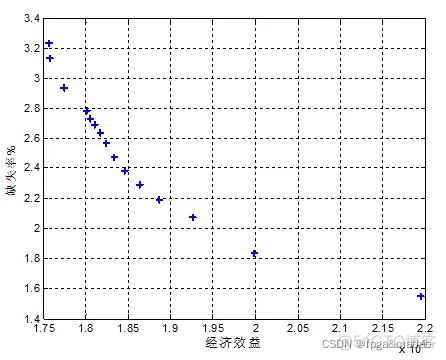
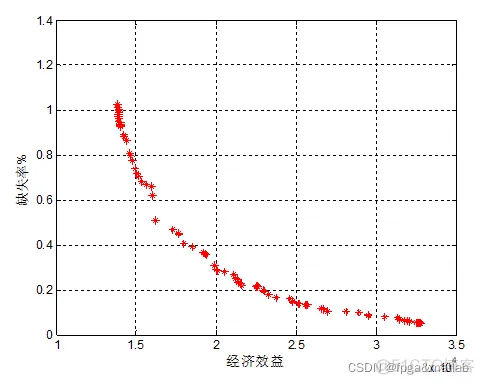
三目标优化的优化目标为:
全寿命周期经济现值,排放水平,负荷容量缺电率;
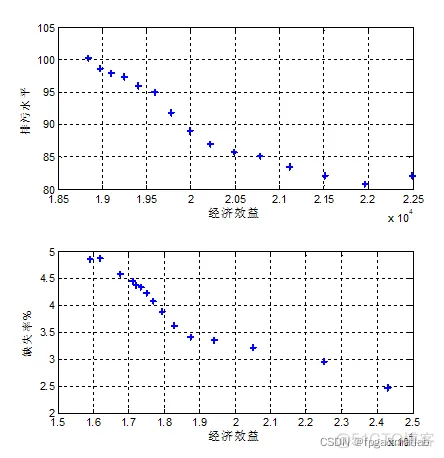
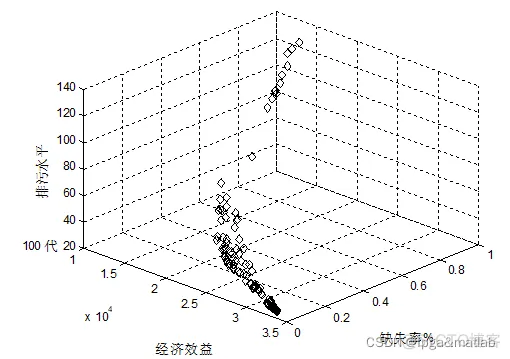
用NSGAii算法,则可以方便的得到其对应的三维图,获得如下的结果:
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删