1.软件版本
matlab2013b
2.本算法理论知识
问题是,假设我有一个收集轨道,上面有5个采集堆,这5个采集堆分别被看作一个4*20的矩阵(下面只有4*10),每个模块(比如:A31和A32的元素含量不同),为了达到采集物品数量和元素含量的要求(比如:需采集5吨和某元素单位质量在65与62之间),求出在每个4*20的矩阵中哪个模块被拿出可以达到要求并找出最优化的轨道?
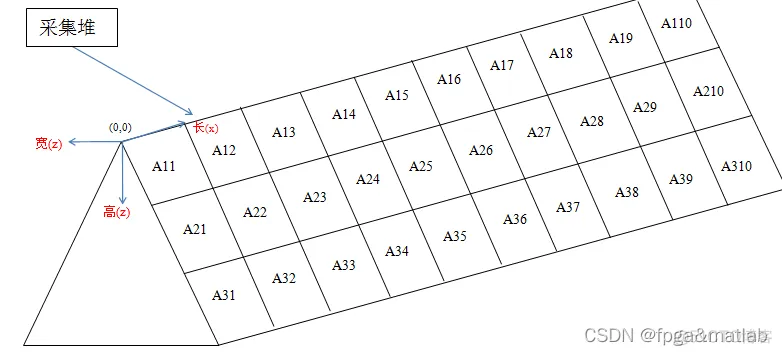
已知数据:
1.每个采集堆的元素含量(在excel表格的 sheet 1)
2.每个采集堆里面模块的坐标,长宽高(米为单位)(在excel表格的 sheet 1)
3.元素含量和采集物品数量的要求 (在excel 表格的 sheet 2), 分别有五种不同含量的最大值和最小值, 还有采集数量的要求,以及误差。
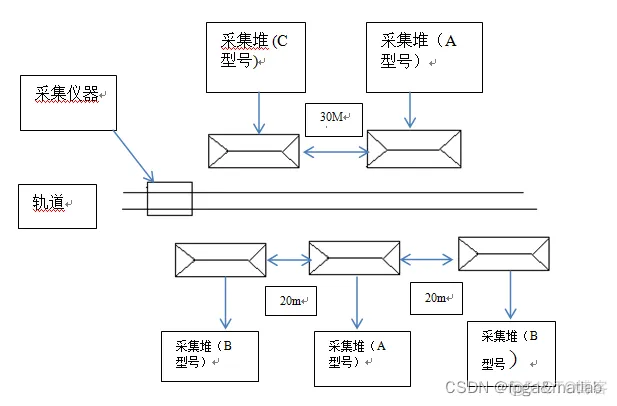
4.在轨道左侧的两个采集堆分别是C型号和A型号的,两个采集堆只见距离30m; 轨道右侧的三个采集堆按照顺序分别是B型号,B型号和C型号,同样每个采集堆之间相距20m。5.采集堆形状附在附录1
高: 10m(A.BC)
每一层宽度和长度不一样,具体数据在excel表格
所以第一行就是三角体体积,剩下的就是梯行体积。
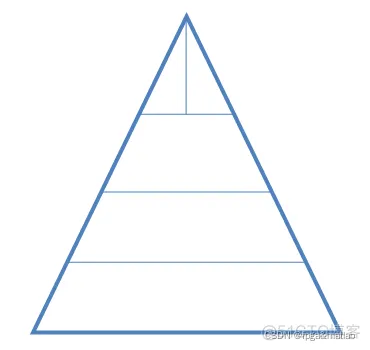
这里其实是一个最优化问题,即满足采集物品的需求,需要对3个类型的5个集散地进行装货,且每次只能取最上面的,如果对于当前位置的物品,如果最少面没有取走,那么只能先取最上面的物品,然后统计装货轨迹的距离,通过优化计算最短距离。
那么,这里解题的关键是计算目标函数,然后使用优化算法对目标函数进行优化处理。本算法的主要目标就是目标函数的设计,这个也是该课题的难点。
首先我们根据上面的需求,建立如下的数学模型:
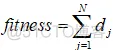
这里,dj表示每一次从一个模块移动到另外一个模块的距离,如果是从一个采集堆移动到另外一个采集堆中,那么则在另外一堆中计算所采集的模块之间的间距。
所以上面的公式为:
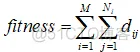
即在不同的采集堆的所有距离之和。这里,需要通过优化考虑不同采集堆之间的移动,以及在每个采集上如何进行模块的采集两个因素。
我们的目标就是使得上面的函数值最小,从而得到采集路线轨迹。
这里,需要考虑的难点有如下几点:
第一:空间轨迹是三维,这个比二维的复杂。
第二:约束条件的建立,我们根据课题的需求,建立如下的约束条件。
2.1 采集规则约束。
即每次只能采集最上面的,如果最上面的没有被取走,那么不能直接采集下面的。
这里,我们使用是数学公式表示如下:
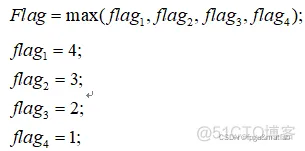
分别对四层的模块进行标记,最上面的为4,如果取走了则直接赋值0,这样,而每次我们只能去标号最大的那个。如果取走了,那么被取走的赋值为0,那么在判断的时候,可以取下面的,如果全部被取走了,则为全0,如果为全零,则这列就不能取值了。即全零表示空。
2.2 满足采集物品数量和元素含量的约束
根据所提供的数据,物品数量的最大值为60000t,误差为1.
而元素含量为得约束条件为:
| 元素1 | 元素2 | 元素3 | 元素4 | 元素5 | |
| 65 | 6 | 4 | 0.077 | 0.1 | 最大值 |
| 62 | 0 | 0 | 0 | 0 | 最小值 |
通过课题所给出的约束条件可知,我们需要通过采集模块,使得最后的总重量为60000,而所采集的物品中的各个元素的所含比例影响满足上面的约束条件。
即上面的约束条件是通过物品的采集,使得总量满足要求,且五个元素的单位质量满足上面的约束,最后使得采集轨迹最短。
所以,通过上面的综合分析,我们所要的数学公式为:

为了方便,我们将所需要的数据,在excel中整理下,将里面一些你用公式编辑的转换为真实的数据。修改的excel文件见新发你的数据,而约束条件则直接在程序中进行设置。
这里,我们假设,设备从一个端点移动到另外一个端点的时候,是逐渐向前移动的,而不是来回移动的。即,设备是一次从轨道的一个端点移动到另外一个端点的(事实上,规定都是依次向运动的)
根据这个假设,我们设计的思路为当每次运动到一堆的时候,首先在这一堆物品上进行采集,由于每堆物品之间的间距远大于每堆内部的各个模块之间的间隔,所以在实际中也不可能在两个不同的堆之间来回切换的抓取模块,这也符合我们上面的假设。
根据上面的假设,我们抓取的顺序为B堆,C堆,A堆,A堆,B堆。
3.核心代码
%根据这个假设,我们设计的思路为当每次运动到一堆的时候,首先在这一堆物品上进行采集,由于%每堆物品之间的间距远大于每堆内部的各个模块
之间的间隔,所以在实际中也不可能在两个不同的%堆之间来回切换的抓取模块,这也符合我们上面的假设。%根据上面的假设,我们抓取的顺序为B堆,
C堆,A堆,A堆,B堆。%这里,我们所使用的算法是局部PSO优化,然后再整体PSO优化的算法,即首先通过再每一堆的采集%的时候进行PSO优化,
并使的各个元素含量满足约束的条件下,得到路径最短的采集轨迹,然后通过%后面三堆重复相同的优化算法,最后第五堆的时候,在做相同的优化
前提下,同时检测总量是否满足%条件,如果不满足进入下一次大迭代循环,然后重复上面的操作,最后得到满足条件的总的采集轨迹。clc;clear;
close all;warning off;pack;addpath 'func\'%*******************************************************************
***************%步骤一:调用数据%步骤一:调用数据Dat = xlsread('Dat\datas.xlsx');%分成ABC三组A_set = Dat( 1:40 ,:);
B_set = Dat(41:80 ,:);C_set = Dat(81:120,:);%A相关数据%坐标A_POS = A_set(:,1:3);%元素含量A_FAC = A_set(:,4:8);
%体积长宽高A_VUM = A_set(:,9:11);%B相关数据%坐标B_POS = B_set(:,1:3);%元素含量B_FAC = B_set(:,4:8);%体积长宽高B_VUM
= B_set(:,9:11);%C相关数据%坐标C_POS = C_set(:,1:3);%元素含量C_FAC = C_set(:,4:8);%体积长宽高C_VUM = C_set(:,9:11);
%**************************************************************************%*********************************
*****************************************%********************************************************************
**************%步骤二:参数初始化%步骤二:参数初始化%约束参数%59999 ~ 60001Mass_all = 60000;Mass_err = 1;
%元素1Mass1_max= 65;Mass1_min= 62;%元素2Mass2_max= 6;Mass2_min= 0;%元素3Mass3_max= 4;Mass3_min= 0;
%元素4Mass4_max= 0.077;Mass4_min= 0;%元素5Mass5_max= 0.1;Mass5_min= 0;%优化算法参数%优化算法参数%迭代次数
Iteration_all = 1;Iteration_sub = 10000;%粒子数目Num_x = 200;%密度P = 2.1;%计算各个模块的质量,单位t%注意
,本课题一个堆中有个四个形状的模块,即三角形,三种梯形,所以我们根据长宽高以及对应的形状计算体积,从而计算质量A_Vulome = func_cal
_volume(A_VUM);B_Vulome = func_cal_volume(B_VUM);C_Vulome = func_cal_volume(C_VUM);%计算每个采集堆的各个模块的质量
A_mass = P*A_Vulome;B_mass = P*B_Vulome;C_mass = P*C_Vulome;%以下根据实际轨迹上的堆的分布来设置maxs_sets =
[B_mass;C_mass;A_mass;A_mass;B_mass];FAC_sets = [B_FAC;C_FAC;A_FAC;A_FAC;B_FAC];%****************************
**********************************************%**************************************************************
************%**********************************************************************************%步骤三:开始优化
运算%步骤三:开始优化运算X_pos{1} = B_POS(:,1);Y_pos{1} = B_POS(:,2);Z_pos{1} = B_POS(:,3);X_pos{2} = C_POS(:,1);
Y_pos{2} = C_POS(:,2);Z_pos{2} = C_POS(:,3);X_pos{3} = A_POS(:,1);Y_pos{3} = A_POS(:,2);Z_pos{3} = A_POS(:,3);
X_pos{4} = A_POS(:,1);Y_pos{4} = A_POS(:,2);Z_pos{4} = A_POS(:,3);X_pos{5} = B_POS(:,1);Y_pos{5} = B_POS(:,2);
Z_pos{5} = B_POS(:,3);%先通过PSO优化需求模型for Num_pso = 4:40%这里没有必要设置太大,设置大了需求量肯定会超过60000,因此,
这个值得大小根据需求量来确定,大概范围即可 Num_pso x = zeros(Num_x,Num_pso); i = 0; %产生能够满足采
集规则的随机粒子数据 for jj = 1:Num_x %产生随机数的时候,必须是先采集第一层,然后才采集第二层,依次类推 %第1
层 index1 = [1:10,41:50,81:90,121:130,161:170]; %第2层 index2 = [1:10,41:50,81:90,121:130,
161:170]+10; %第3层 index3 = [1:10,41:50,81:90,121:130,161:170]+20; %第4层 index4 =
[1:10,41:50,81:90,121:130,161:170]+30; %根据采集规则产生随机数 %根据采集规则产生随机数
%根据采集规则产生随机数 index = [index1;index2;index3;index4]; i = 0; while i < Num_pso
i = i + 1; if i> 1 for j = 1:50; index(IS(j),ind(1)) =
9999; end end for j = 1:50; [VS,IS(j)] = min(inde
x(:,j)); tmps(1,j) = index(IS(j),j); end ind = randperm(40);
a(i) = tmps(ind(1)); if a(i) == 9999 i = i-1; end
end x(jj,:) = a; end n = Num_pso; F =
fitness_mass(x,maxs_sets,Mass_all); Fitness_tmps1 = F(1); Fitness_tmps2 = 1;
for i=1:Num_x if Fitness_tmps1 >= F(i) Fitness_tmps1 = F(i);
Fitness_tmps2 = i; end end xuhao = Fitness_tmps2; Tour_pbes
t = x; %当前个体最优 Tour_gbest = x(xuhao,:) ;
%当前全局最优路径 Pb = inf*ones(1,Num_x); %个体最优记录 Gb
= F(Fitness_tmps2); %群体最优记录 xnew1 = x; N
= 1; while N <= Iteration_sub %计算适应度 F = fitness_mass(x,maxs_sets,Mass_all);
for i=1:Num_x if F(i)<Pb(i) %将当前值赋给新的最佳值 Pb(i)=F(i);
Tour_pbest(i,:)=x(i,:); end if F(i)<Gb Gb=F(i);
Tour_gbest=x(i,:); end end Fitness_tmps1 = Pb(1); Fitness_tmps2 = 1;
for i=1:Num_x if Fitness_tmps1>=Pb(i) Fitness_tmps1=Pb(i); Fitness_tmp
s2=i; end end nummin = Fitness_tmps2; %当前群体最优需求量差 Gb(N)
= Pb(nummin); for i=1:Num_x %与个体最优进行交叉 c1 = round(rand*(n-2))+1;
c2 = round(rand*(n-2))+1; while c1==c2 c1 = round(rand*(n-2))+1;
c2 = round(rand*(n-2))+1; end chb1 = min(c1,c2); chb2 = max(c1,c2);
cros = Tour_pbest(i,chb1:chb2); %交叉区域元素个数 ncros= size(cros,2);
%删除与交叉区域相同元素 for j=1:ncros for k=1:n if xnew1(i,k)==cros(j)
xnew1(i,k)=0; for t=1:n-k temp=xnew1(i
,k+t-1); xnew1(i,k+t-1)=xnew1(i,k+t); xnew1(i,k+t)=temp;
end end end end xnew = xnew1; %插入交叉区域
for j=1:ncros xnew1(i,n-ncros+j) = cros(j); end %判断产生需求量差是否变小
masses=0; masses = sum(maxs_sets(xnew1(i,:))); if F(i)>masses
x(i,:) = xnew1(i,:); end %与全体最优进行交叉 c1 = round(rand*(n-2))+1;
c2 = round(rand*(n-2))+1; while c1==c2 c1=round(rand*(n-2))+1;
c2=round(rand*(n-2))+1; end chb1 = min(c1,c2);
chb2 = max(c1,c2); %交叉区域矩阵
cros = Tour_gbest(chb1:chb2); %交叉区域元素个数 ncros= size(cros,2);
%删除与交叉区域相同元素 for j=1:ncros for k=1:n
if xnew1(i,k)==cros(j) xnew1(i,k)=0;
for t=1:n-k temp=xnew1(i,k+t-1);
xnew1(i,k+t-1)=xnew1(i,k+t); xnew1(i,k+t)=temp;
end end end end
xnew = xnew1; %插入交叉区域 for j=1:ncros xnew1(i,n-ncros+j) = cros(j);
end %判断产生需求量差是否变小 masses=0; masses = sum(maxs_sets(xnew1(i,:)));
if F(i)>masses x(i,:)=xnew1(i,:); end %进行变异操作
c1 = round(rand*(n-1))+1; c2 = round(rand*(n-1))+1;
temp = xnew1(i,c1); xnew1(i,c1) = xnew1(i,c2); xnew1(i,c2) = temp;
%判断产生需求量差是否变小 masses=0; masses = sum(maxs_sets(xnew1(i,:)));
if F(i)>masses x(i,:)=xnew1(i,:); end end Fitness_tmps1=F(1);
Fitness_tmps2=1; for i=1:Num_x if Fitness_tmps1>=F(i) Fitness_tmps1=F(i);
Fitness_tmps2=i; end end xuhao = Fitness_tmps2; L_best(N) = min(F);
%当前全局最优需求量 Tour_gbest = x(xuhao,:); N = N + 1; end
%判断含量是否满足要求 for ii = 1:5 Fac_tmps(ii) = sum(FAC_sets(Tour_gbest,ii)'.*maxs_sets(Tour_gbest))
/sum(maxs_sets(Tour_gbest)); end if (Fac_tmps(1) >= Mass1_min & Fac_tmps(1) <= Mass1_max) &...
(Fac_tmps(2) >= Mass2_min & Fac_tmps(2) <= Mass2_max) &...
(Fac_tmps(3) >= Mass3_min & Fac_tmps(3) <= Mass3_max) &...
(Fac_tmps(4) >= Mass4_min & Fac_tmps(4) <= Mass4_max) &...
(Fac_tmps(5) >= Mass5_min & Fac_tmps(5) <= Mass5_max)
flag(Num_pso-3) = 1; else flag(Num_pso-3) = 0; end Mass_fig(Num_pso-3) = min(L_best);
Mass_Index{Num_pso-3}= Tour_gbest ;endfigure;plot(Mass_fig,'b-o');xlabel('采集模块个数');
ylabel('需求量计算值和标准需求量的差值关系图');save temp\result1.mat Mass_fig Mass_Index flag1.2.3.4.5.6.7.8.9.
10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.36.37.38.39.40.41.42.43.44.
45.46.47.48.49.50.51.52.53.54.55.56.57.58.59.60.61.62.63.64.65.66.67.68.69.70.71.72.73.74.75.76.77.78.79.
80.81.82.83.84.85.86.87.88.89.90.91.92.93.94.95.96.97.98.99.100.101.102.103.104.105.106.107.108.109.110.
111.112.113.114.115.116.117.118.119.120.121.122.123.124.125.126.127.128.129.130.131.132.133.134.135.136.
137.138.139.140.141.142.143.144.145.146.147.148.149.150.151.152.153.154.155.156.157.158.159.160.161.162.
163.164.165.166.167.168.169.170.171.172.173.174.175.176.177.178.179.180.181.182.183.184.185.186.187.188.
189.190.191.192.193.194.195.196.197.198.199.200.201.202.203.204.205.206.207.208.209.210.211.212.213.214.
215.216.217.218.219.220.221.222.223.224.225.226.227.228.229.230.231.232.233.234.235.236.237.238.239.240.
241.242.243.244.245.246.247.248.249.250.251.252.253.254.255.256.257.258.259.260.261.262.263.264.265.266.
267.268.269.270.271.272.273.274.275.276.277.278.279.280.281.282.283.284.285.286.287.288.289.290.291.292.
293.294.295.296.297.298.299.300.301.302.303.304.305.306.307.308.309.310.311.312.313.314.315.316.317.318.
319.320.321.322.323.324.325.326.327.328.329.330.331.332.333.334.335.336.337.338.339.340.341.342.343.344.
345.346.347.348.349.350.351.352.353.354.355.356.357.358.359.4.操作步骤与仿真结论
首先,运行程序run_first.m,搜索所有采集方法得到的需求量为59999~60001之间的采集组合。并保存仿真结果。
这个步骤仿真结果如下所示:
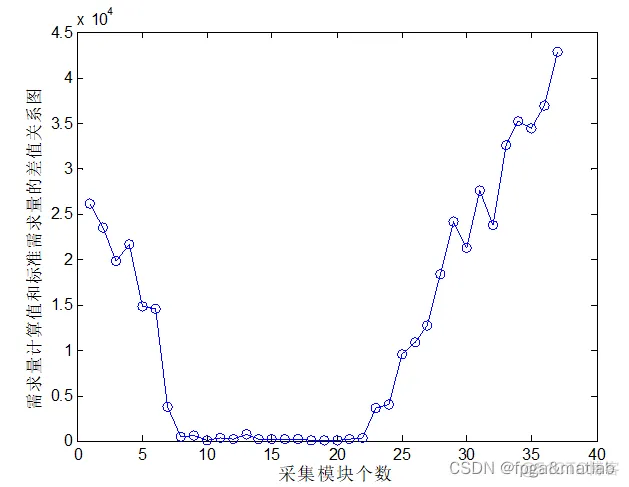
通过这个步骤将优化出符合采集规则且符合元素含量,并满足需求量的模块集合,然后运行run_second.m,进行轨迹优化。
最后得到的优化记过,即满足条件下的最短轨迹长度
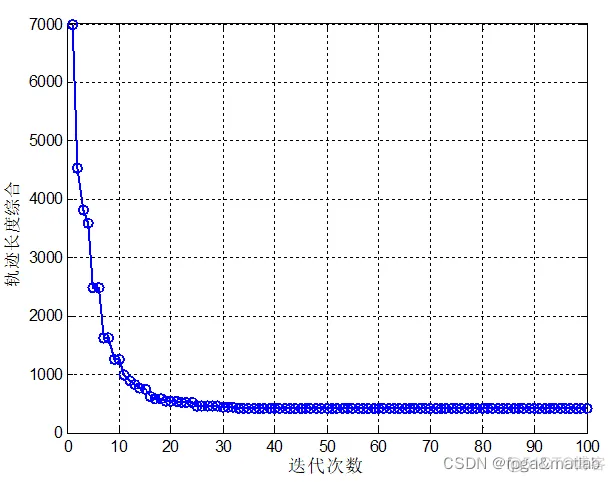
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删