1.算法描述
强化学习通常包括两个实体agent和environment。两个实体的交互如下,在environment的statestst下,agent采取actionatat进而得到rewardrtrt 并进入statest+1st+1。Q-learning的核心是Q-table。Q-table的行和列分别表示state和action的值,Q-table的值Q(s,a)Q(s,a)衡量当前states采取actiona到底有多好。
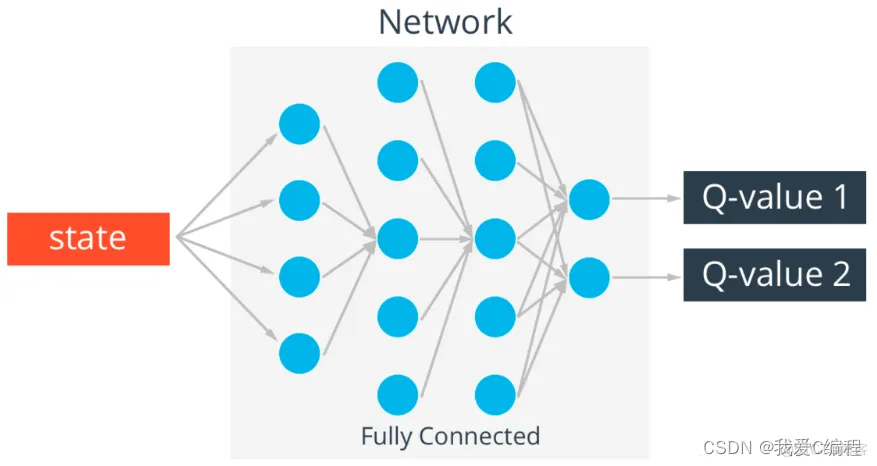
在每一时刻,智能体观测环境的当下状态并选择一个动作,这会导致环境转移到一个新的状态,与此同时环境会返回给智能体一个奖励,该奖励反映了动作所导致的结果。在倒立摆任务中,每一个时间步的奖励均为+1,但是一旦小车偏离中心超过4.8个单位或者杆的倾斜超过15度,任务就会终止。因此,我们的目标是使得该任务能够尽可能地运行得更久,以便获得更多的收益。原始倒立摆任务中,智能体的输入包含4个实数(位置,速度等),但实际上,神经网络可以直接通过观察场景来完成任务,所以我们可以直接使用以小车为中心的屏幕补丁作为输入。严格来说,我们设计的状态是当前屏幕补丁与上一个屏幕补丁的差值,这使得智能体能够从一张图像中推断出杆的速度。
为了训练DQN,我们将使用经验回放池(experience replay memory)来存储智能体所观测到的环境状态转移情况,在之后的训练中我们可以充分利用这些数据。通过对经验回放池中的数据进行随机采样,组成一个批次的转移情况是互不相关(decorrelated)的,这极大地提升了DQN训练的性能和稳定性。
主要步骤如下:
采样得到一个批次的样本,将这些样本对应的张量连接成一个单独的张量;
分别利用策略Q网络与目标Q网络计算 与Q(st,at)与V(st+1)=maxaQ(st+1,a) ,利用它们计算损失函数.。另外,如果 s 为终止状态,则令 V(s)=0
更新Q网络参数。目标Q网络的参数每隔一段时间从主Q网络处固定而来,在本例中,我们在每个episode更新一次目标Q网络。
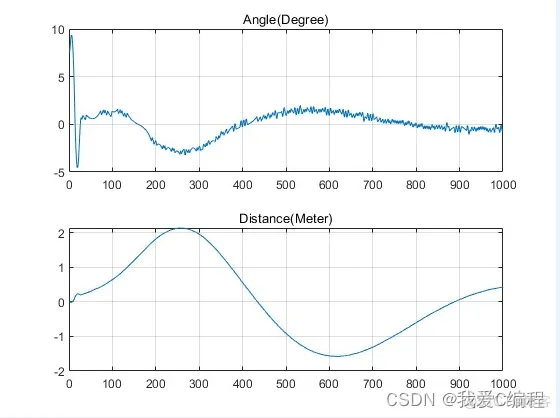
2.仿真效果预览
matlab2022a仿真结果如下:
3.MATLAB部分代码预览
count=0;
failure=0;
failReason=0;
lfts = 1;
newSt = inistate;
inputs = newSt./NF;
lc = Initlc;
la = Initla;
xhist=newSt;
%计算newAction
ha = inputs*wa1;
g = (1 - exp(-ha))./(1 + exp(-ha));
va = g*wa2;
newAction = (1 - exp(-va))./(1 + exp(-va));
%计算J
inp=[inputs newAction];
qc=inp*wc1;
p = (1 - exp(-qc))./(1 + exp(-qc));
J=p*wc2;
Jprev = J;
while(lfts<Tit), %内部循环开始
if (rem(lfts,500)==0),
disp(['It is ' int2str(lfts) ' time steps now......']);
end
%生成控制信号
if (newAction >= 0)
sgnf = 1;
else
sgnf = -1;
end
u = Mag*sgnf; %bang-bang control
%Plug in the model
[T,Xf]=ode45('cartpole_model',[0 tstep],newSt,[],u);
a=size(Xf);
newSt=Xf(a(1),:);
inputs=newSt./NF; %input normalization
%计算newAction
ha = inputs*wa1;
g = (1 - exp(-ha))./(1 + exp(-ha));
va = g*wa2;
newAction = (1 - exp(-va))./(1 + exp(-va));
%calculate new J
inp=[inputs newAction];
qc=inp*wc1;
p = (1 - exp(-qc))./(1 + exp(-qc));
J=p*wc2;
xhist=[xhist;newSt];
%%===========================================================%%
%%求取强化信号r(t),即reinf %%
%%===========================================================%%
if (abs(newSt(1)) > FailTheta)
reinf = 1;
failure = 1;
failReason = 1;
elseif (abs(newSt(3)) > Boundary)
reinf = 1;
failure = 1;
failReason = 2;
else
reinf = 0;
end
%%================================%%
%% learning rate update scheme %%
%%================================%%
if (rem(lfts,5)==0)
lc = lc - 0.05;
la = la - 0.05;
end
if (lc<0.01)
lc=0.005;
end
if (la<0.01)
la=0.005;
end
%%================================================%%
%% internal weights updating cycles for critnet %%
%%================================================%%
cyc = 0;
ecrit = alpha*J-(Jprev-reinf);
Ec = 0.5 * ecrit^2;
while (Ec>Tc & cyc<=Ncrit),
gradEcJ=alpha*ecrit;
%----for the first layer(input to hidden layer)-----------
gradqwc1 = [inputs'; newAction];
for i=1:N_Hidden,
gradJp = wc2(i);
gradpq = 0.5*(1-p(i)^2);
wc1(:,i) = wc1(:,i) - lc*gradEcJ*gradJp*gradpq*gradqwc1;
end
%----for the second layer(hidden layer to output)-----------
gradJwc2=p';
wc2 = wc2- lc*gradEcJ*gradJwc2;
%----compute new J----
inp=[inputs newAction];
qc=inp*wc1;
p = (1 - exp(-qc))./(1 + exp(-qc));
J=p*wc2;
cyc = cyc +1;
ecrit = alpha*J-(Jprev-reinf);
Ec = 0.5 * ecrit^2;
end % end of "while (Ec>0.05 & cyc<=Ncrit)"
%normalization weights for critical network
if (max(max(abs(wc1)))>1.5)
wc1=wc1/max(max(abs(wc1)));
end
if max(max(abs(wc2)))>1.5
wc2=wc2/max(max(abs(wc2)));
end
%%=============================================%%
%% internal weights updating cycles for actnet %%
%%=============================================%%
cyc = 0;
eact = J - Uc;
Ea = 0.5*eact^2;
while (Ea>Ta & cyc<=Nact),
graduv = 0.5*(1-newAction^2);
gradEaJ = eact;
gradJu = 0;
for i=1:N_Hidden,
gradJu = gradJu + wc2(i)*0.5*(1-p(i)^2)*wc1(WC_Inputs,i);
end
%----for the first layer(input to hidden layer)-----------
for (i=1:N_Hidden),
gradvg = wa2(i);
gradgh = 0.5*(1-g(i)^2);
gradhwa1 = inputs';
wa1(:,i)=wa1(:,i)-la*gradEaJ*gradJu*graduv*gradvg*gradgh*gradhwa1;
end
%----for the second layer(hidden layer to output)-----------
gradvwa2 = g';
wa2=wa2-la*gradEaJ*gradJu*graduv*gradvwa2;
%----compute new J and newAction-------
ha = inputs*wa1;
g = (1 - exp(-ha))./(1 + exp(-ha));
va = g*wa2;
newAction = (1 - exp(-va))./(1 + exp(-va));
inp=[inputs newAction];
qc=inp*wc1;
p = (1 - exp(-qc))./(1 + exp(-qc));
J=p*wc2;
cyc = cyc+1;
eact = J - Uc;
Ea = 0.5*eact^2;
end %end of "while (Ea>Ta & cyc<=Nact)"
if ~failure
Jprev=J;
else
break; %another trial 即跳出“while(lfts<Tit),”
end
lfts=lfts+1;
end %end of "while(lfts<Tit)" 结束内部循环
msgstr1=['Trial # ' int2str(trial) ' has ' int2str(lfts) ' time steps.'];
msgstr21=['Trial # ' int2str(trial) ' has successfully balanced for at least '];
msgstr22=[msgstr21 int2str(lfts) ' time steps '];
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删