探索Abaqus中的Superelasticity超弹性材料

Abaqus中提供的超弹性模型Super Elasticity Model：

用于模拟经历固-固、马氏体相变并表现出超弹性响应的镍钛合金类材料；

可用于模拟应力诱导下奥氏体向马氏体的转变、应力诱导马氏体向奥氏体转变、马氏体重取向和形状固定过程;；

基于Auricchio and Taylor (1996, 1997)的工作。

依据上述描述，Superelasticity材料模型可能更多的用于定义形状记忆合金。

1. 材料的行为

超弹性模型superelastic model 是基于相变材料的单轴应力-应变响应，如图1。这些材料(如镍钛合金)在无加载条件下处于奥氏体相。假定奥氏体遵循各向同性线弹性。加载超过一定应力后，材料由奥氏体开始向马氏体转变。马氏体也假定遵循各向同性线弹性。在相变过程中，根据奥氏体和马氏体的弹性常数计算弹性性能，遵循混合规律:

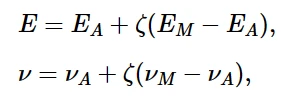
   材料的综合弹性模量和泊松比
 

其中，ζ为马氏体的比例，EA为奥氏体杨氏模量，EM为马氏体杨氏模量，νA为奥氏体泊松比，νM为马氏体泊松比。

经过一定的应力后，奥氏体完全转变为马氏体，随后马氏体发生弹性变形。因此，当马氏体分数为0时，变形遵循奥氏体的弹性常数，当马氏体分数为1时，变形遵循马氏体的弹性常数(完全转变)。卸载后，马氏体转变回奥氏体，相变应变完全恢复。然而，发生反向转变的应力与发生奥氏体向马氏体转变的应力是不同的。

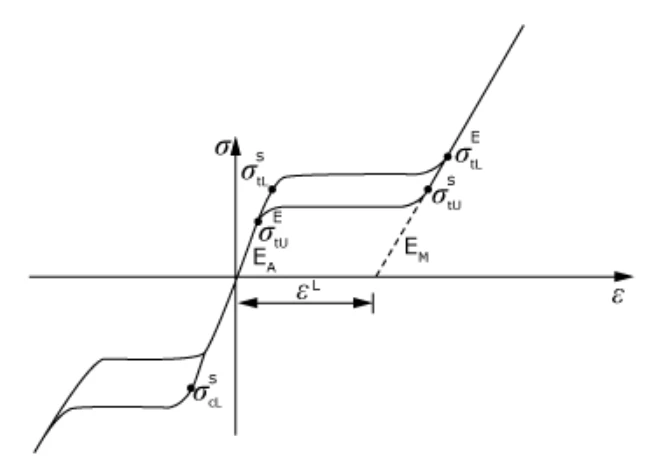
   图1 材料响应
 

在该模型中，假定总应变增量Δ ε为弹性应变增量Δεe1和转变应变增量Δεtr之和：

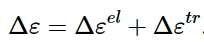
转变应变增量按以下流动法则计算:

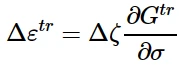
   其中Gtr为转变势能
 

假设转变势遵循Drucker-Prager形式：

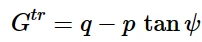
   转变势
 

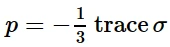
   等效压应力
 

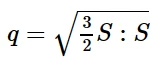
   Mises等效应力
 

变换表面F tr 也假定遵循Drucker-Prager形式，且随温度t线性变化:

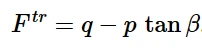
角β和ψ由用户提供的拉伸和压缩转换应力水平、单轴转换应变和体积转换应变计算得到。

可以指定在参考温度t0下发生转变的应力水平。假设这些应力水平随温度线性变化，如图2所示。但是材料数据不能指定为温度或场变量的函数。

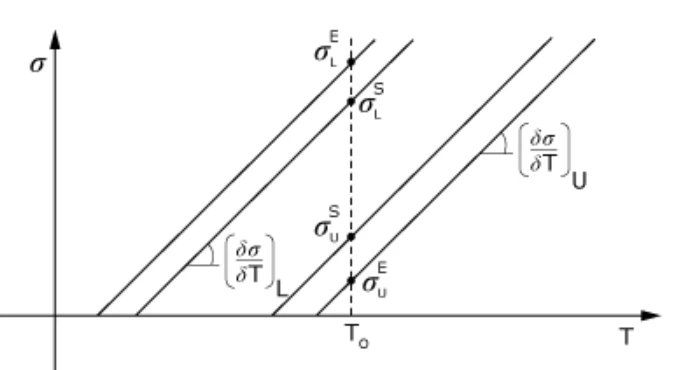
   应力的温度响应
 

2. Abaqus参数定义：

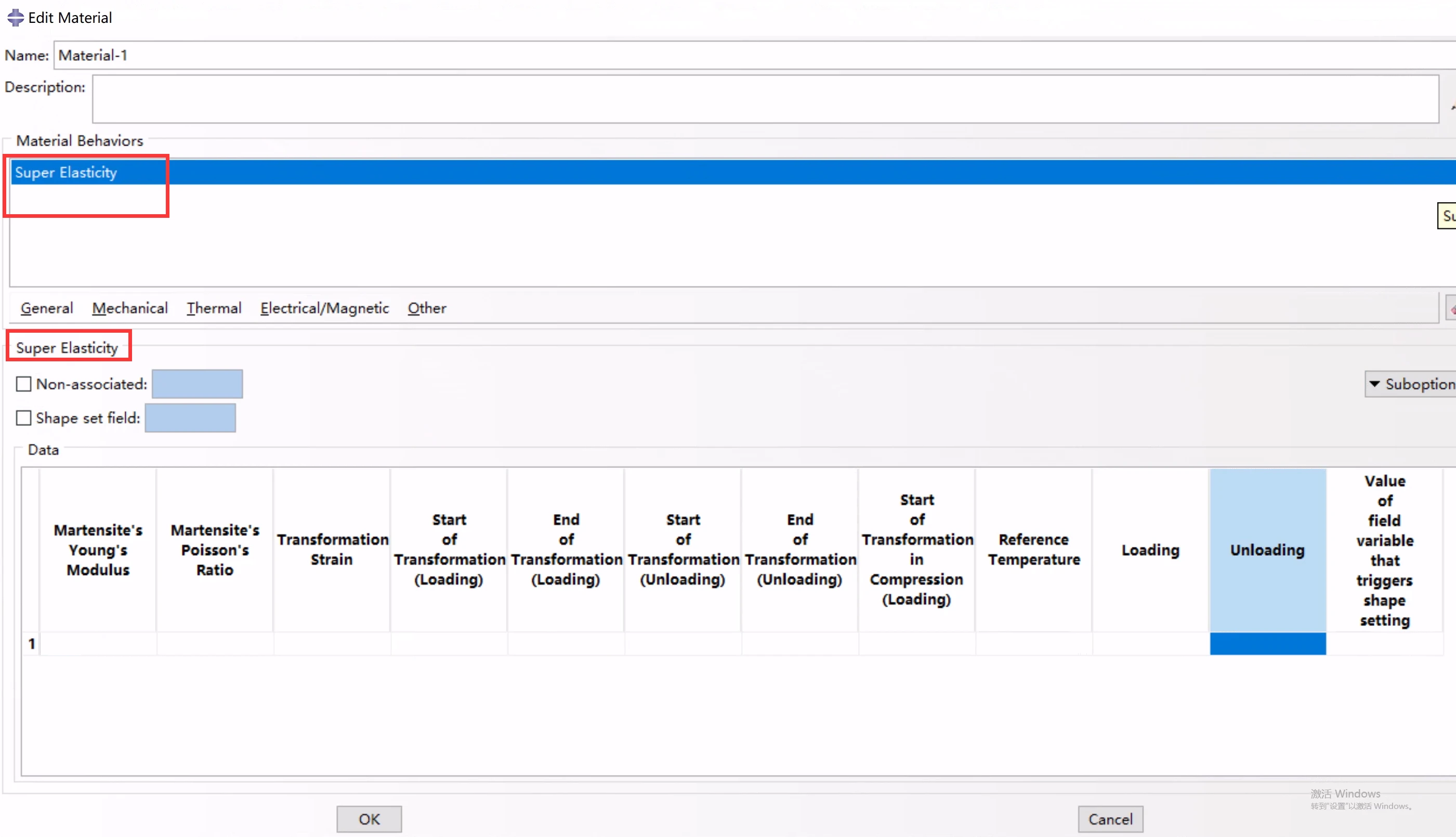
   SUPERELASTIC
 

其中:

选项 NON ASSOCIATED: 将此参数为体积变换应变，若省略此参数，则假定体积转变应变等于单轴转变应变；

选项SHAPE SET FIELD：将此参数为驱动形状固定过程的用户自定义场变量的编号。

数据输入Data：

1. Young's modulus of martensite, EM. 马氏体的杨氏模量
2. Poisson's ratio of martensite, νM. 马氏体泊松比
3. Uniaxial transformation strain, εL.单轴转变应变
4. Stress at which the transformation begins during loading in tension, σStL.在拉伸加载过程中，转变开始时的应力
5. Stress at which the transformation ends during loading in tension, σEtL.拉伸加载过程中转变结束时的应力
6. Stress at which the reverse transformation begins during unloading in tension, σStU.在拉卸载过程中开始反向转变的应力
7. Stress at which the reverse transformation ends during unloading in tension, σEtU.在拉伸卸载过程中，反向转换结束时的应力
8. Stress at which the transformation begins during loading in compression, as a positive value, σScL.压缩加载过程中转变开始时的应力，取正值
9. Reference temperature, T0.参考温度
10. Slope of the stress versus temperature curve for loading, (δσ/δT)L 加载时应力与温度曲线的斜率（可见图2）
11. Slope of the stress versus temperature curve for unloading, (δσ/δT)U. 卸载时应力与温度曲线的斜率（可见图2）
12. 最后一项，将触发形状固定过程的用户定义的场变量的值。它应该与SHAPE SET FIELD选项一起使用。通过将所有状态变量设置为零来完成形状固定。该过程在Abaqus/Standard和Abaqus/Explicit之间有所不同。在Abaqus/Standard中，必须定义驱动删除和重新激活单元形状固定过程的场变量。在Abaqus/Explicit中，只需要指定退火过程。

嘿，有没有发现，以上定义还是不完整，因为根据理论，还需要奥氏体的杨氏模量和泊松比。因此，由于假设奥氏体为线弹性，采用线弹性定义奥氏体的材料弹性模量和泊松比。即，Superelastic须与Elastic联合使用。

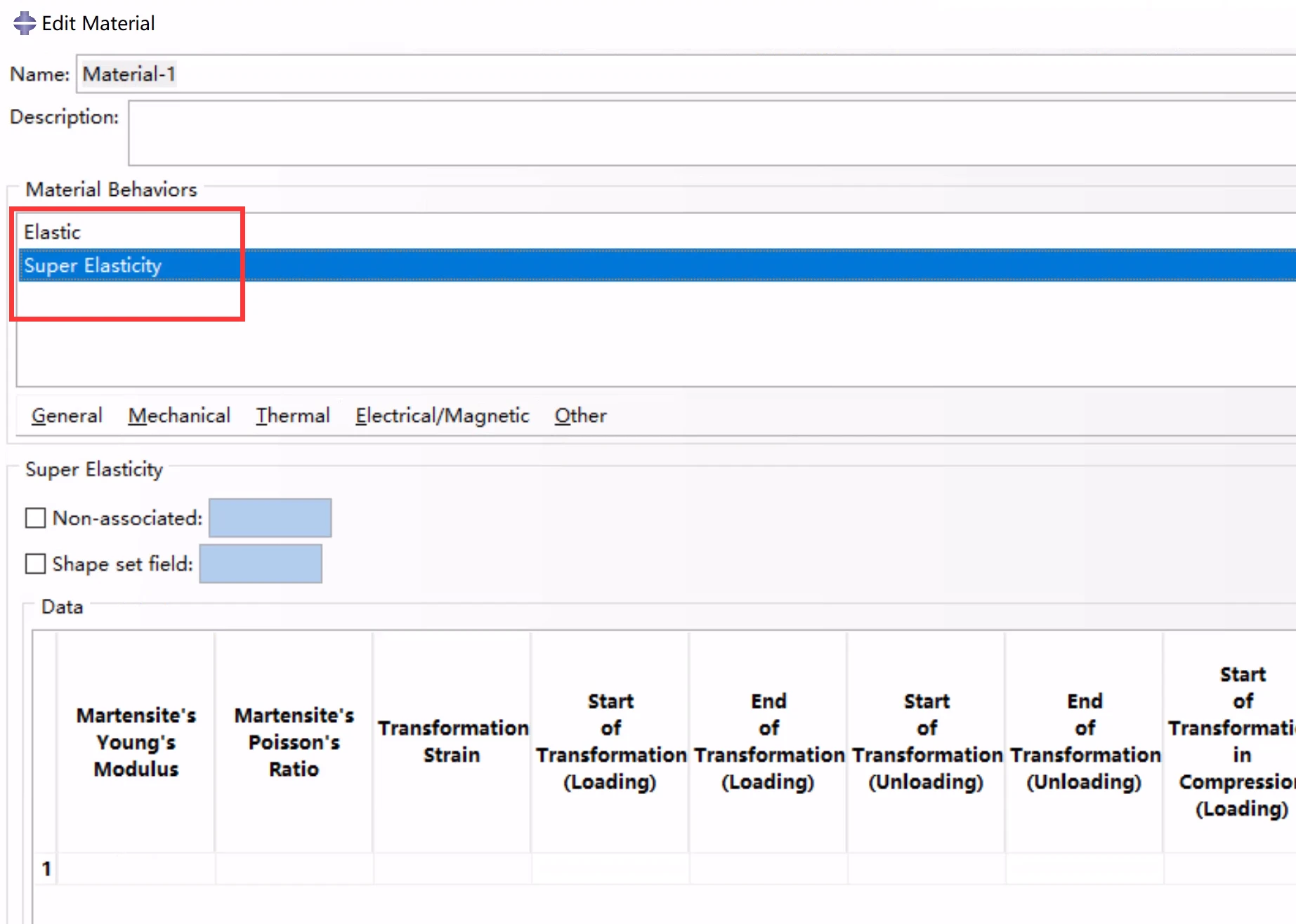
   联合使用定义
 

3. 单元和输出

超弹性Superelasticity可以与Abaqus中的任何应力/位移单元一起使用。

除了Abaqus中可用的标准输出标识符之外，以下变量可用于超弹性Superelasticity模型:

• TE：Transformation strain tensor.转变应变张量
• TEEQ：Equivalent transformation strain.等效转变应变
• TEVOL：Volumetric transformation strain.体积转变应变。
• MVF：Fraction of martensite.马氏体的比例分数

免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删