ABAQUS基础培训最终篇：随机振动分析

随机振动分析_概率、统计问题——谱分析方法——标准方差1&的位移力和应力——计算结果用来评价结构随机振动疲劳寿命

随机振动用处

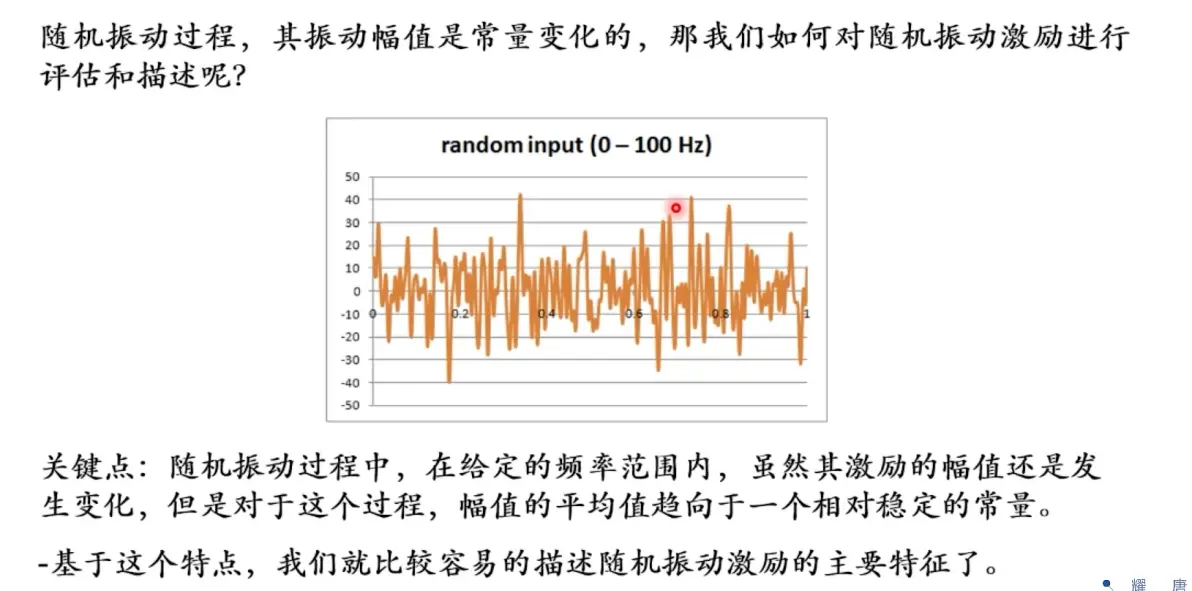
随机振动过程，载荷倾向于稳定

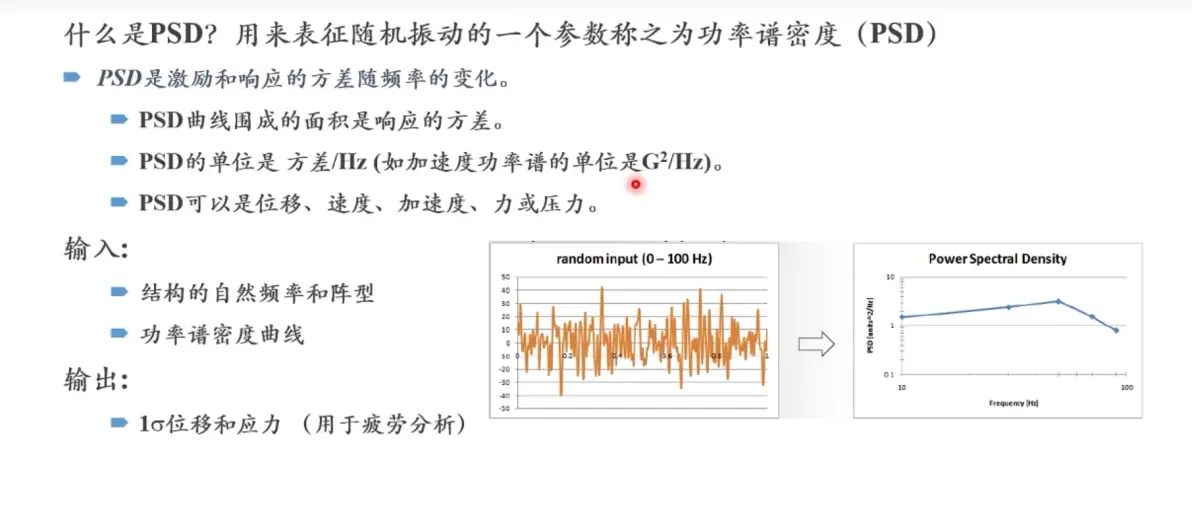
PSD Power Spectrum Density

时域信号 时间——幅值

时域——频域，傅里叶变化

输入与输出

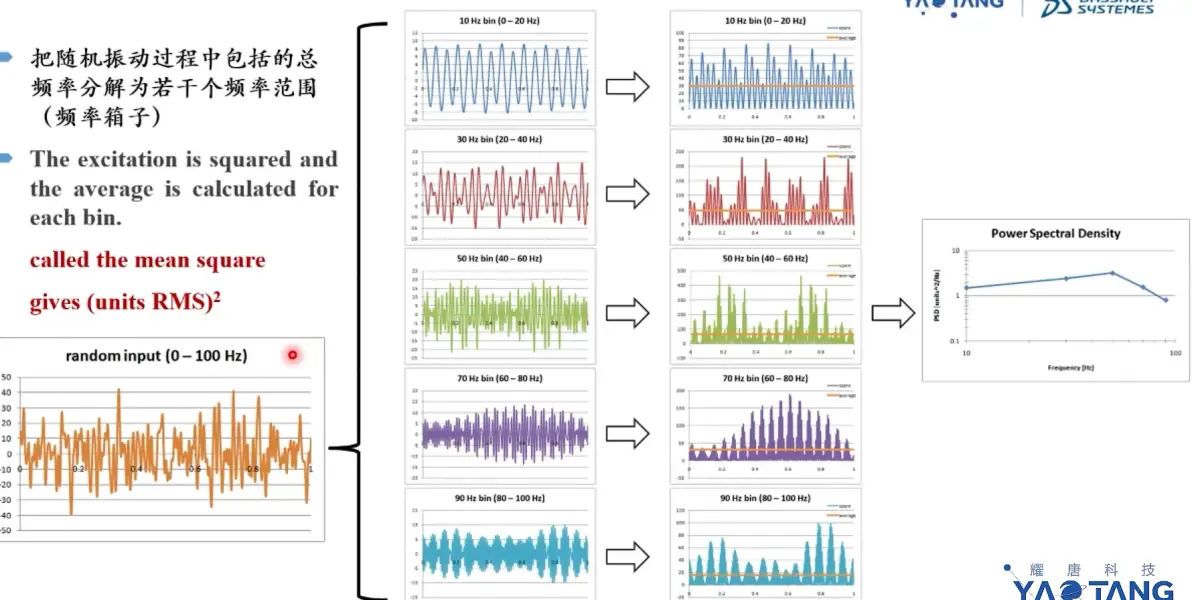
频率分解——主要能量区——考虑前处理成本以及准确率

谱分析与随机振动：谱分析——采集结果，随机振动——统计类概率问题

随机振动特点

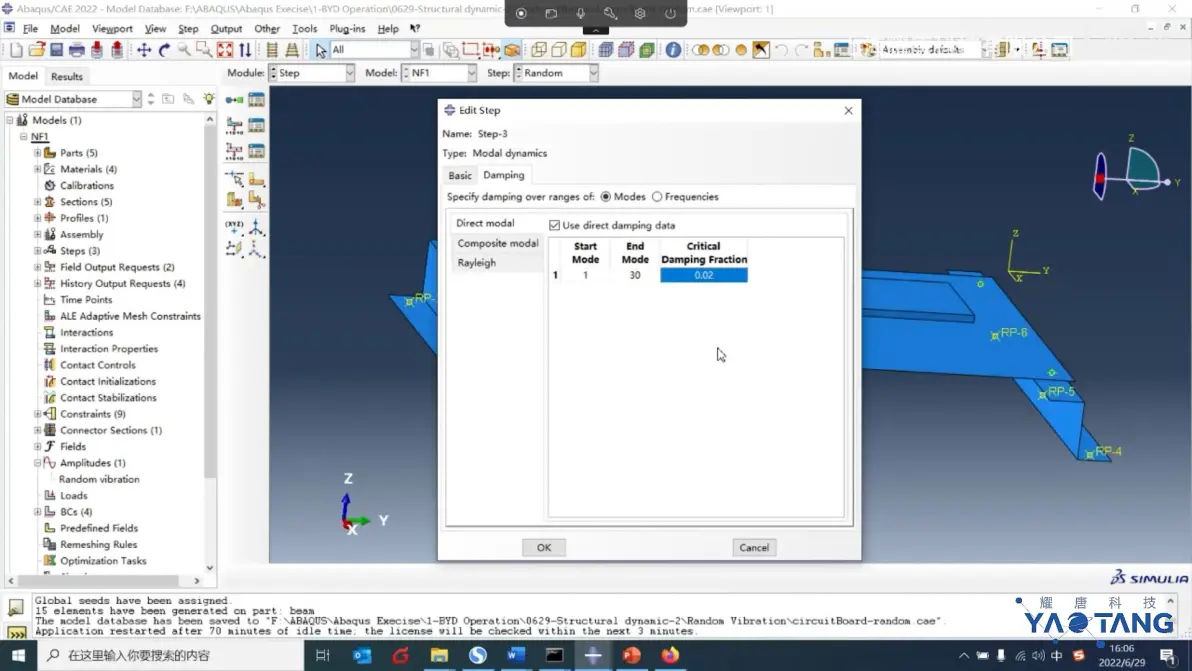
考虑阻尼影响

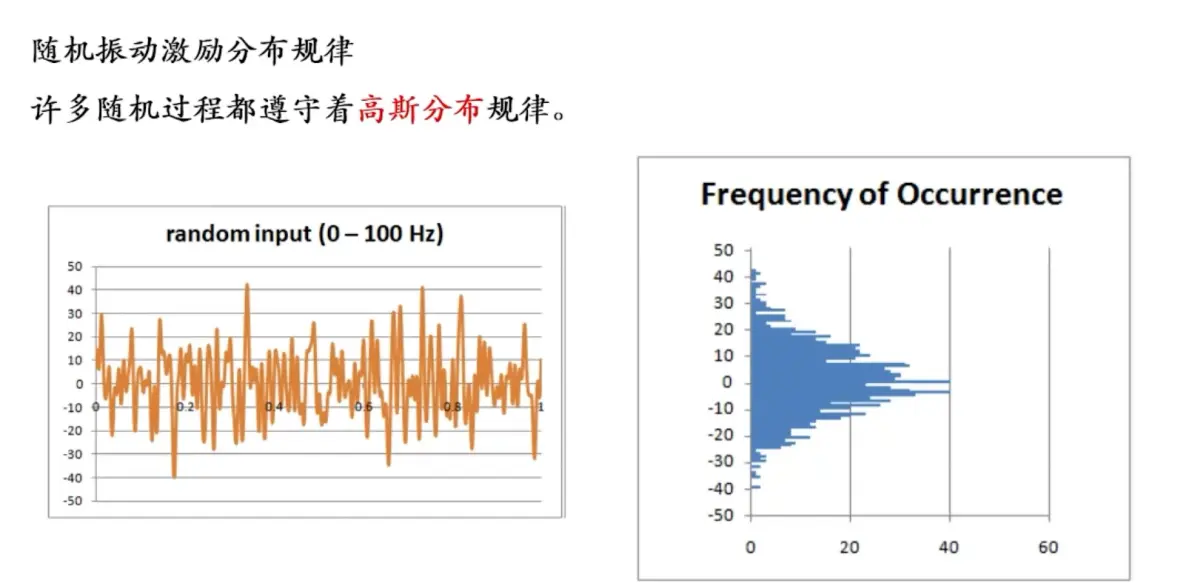
分布规律：高斯分布

一般计算3sigma作为计算上限

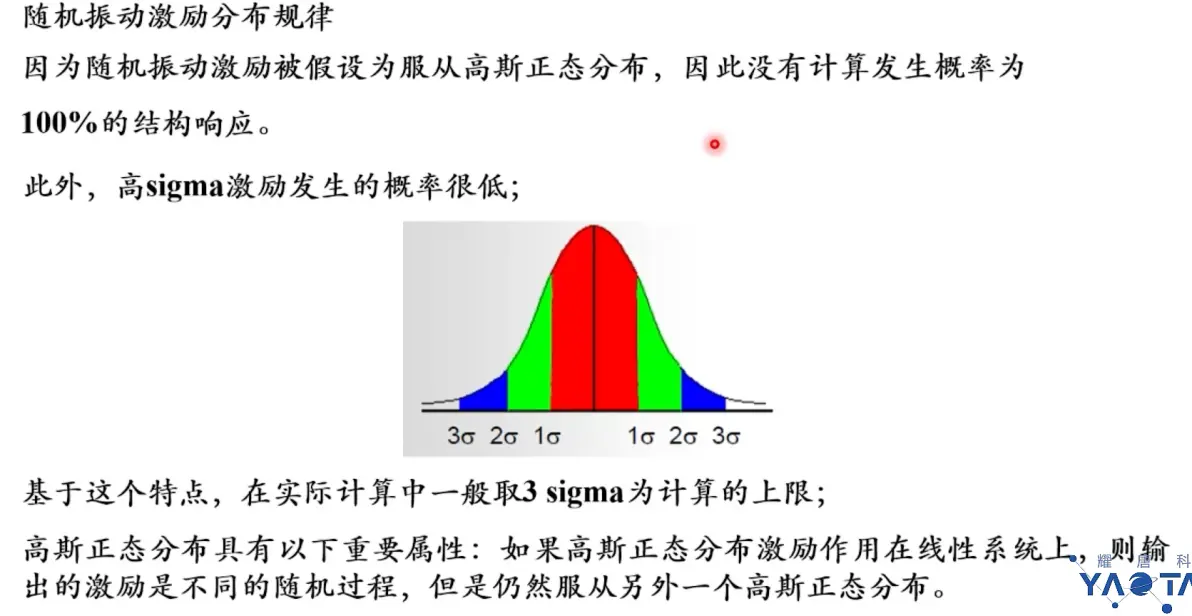
1-3sigma分别覆盖范围

瞬态动力学——输入时间函数载荷，输出随时间变化的位移，应力应变

瞬态——时间

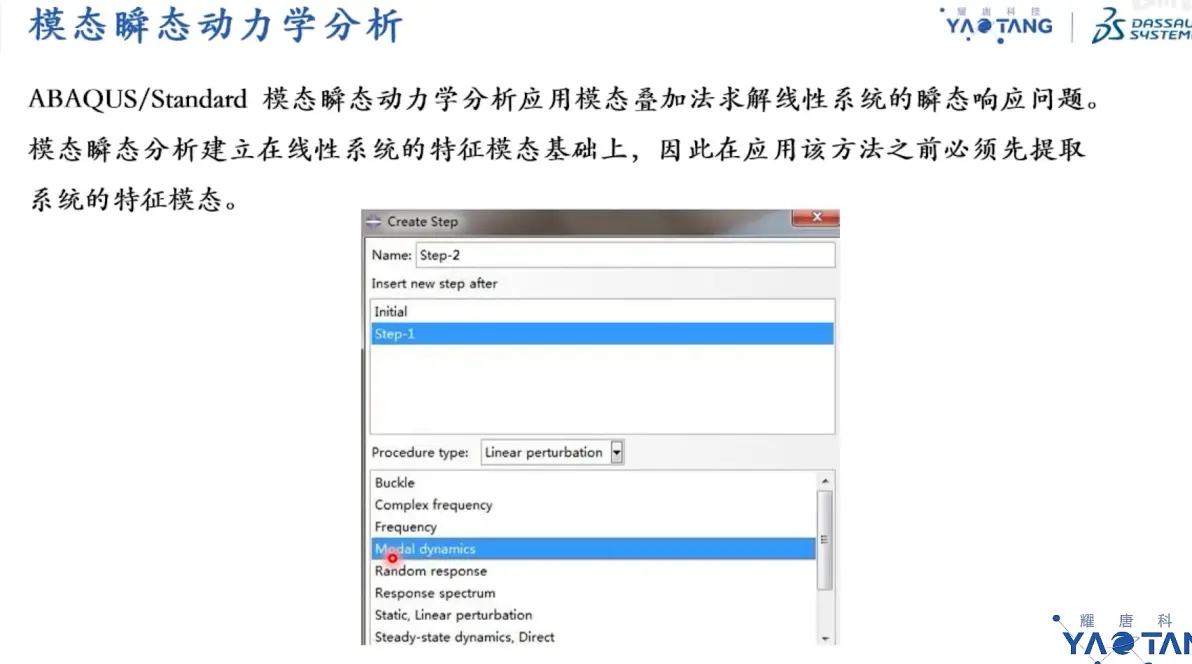
模态叠加法：模态矩阵质量矩阵

完全积分法：完整矩阵

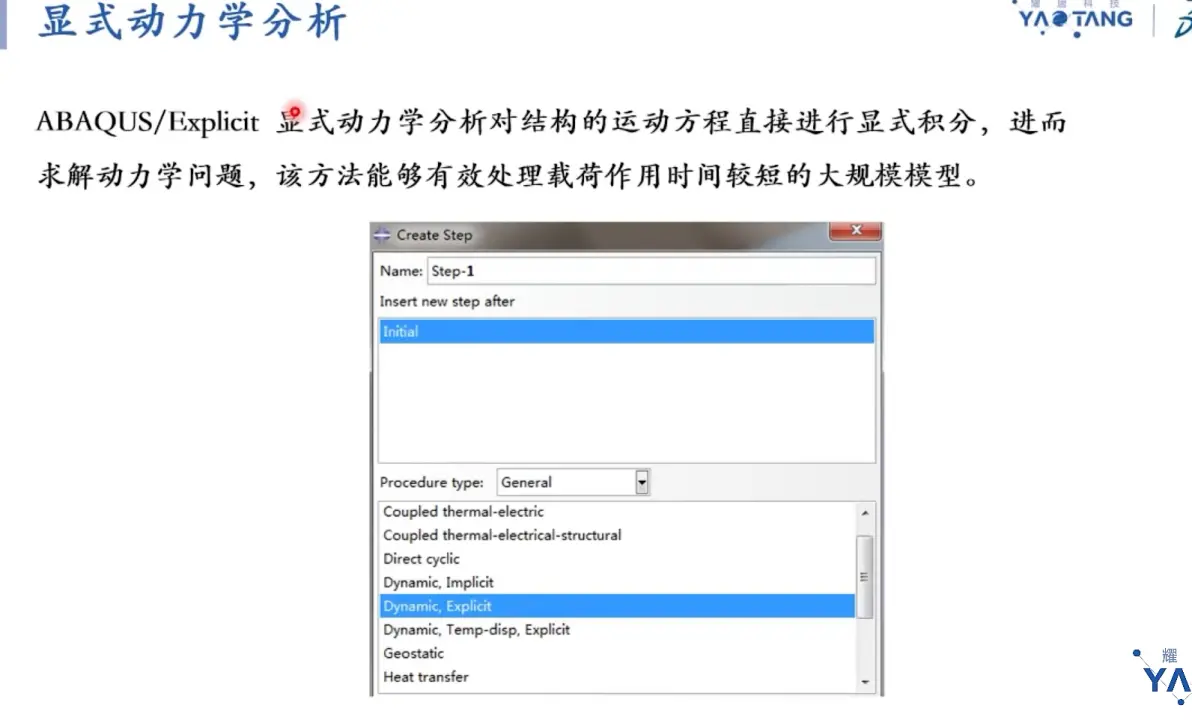
隐式动力学——强非线性瞬态响应分析

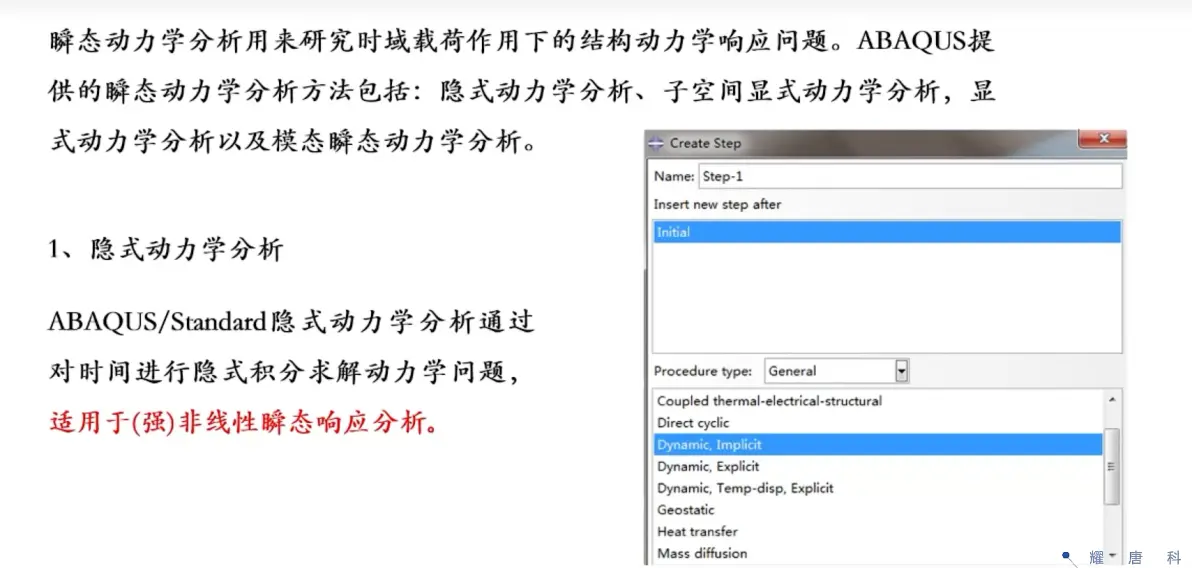
时间指的是运动真实时间（冲击0.01s）可考虑大变形

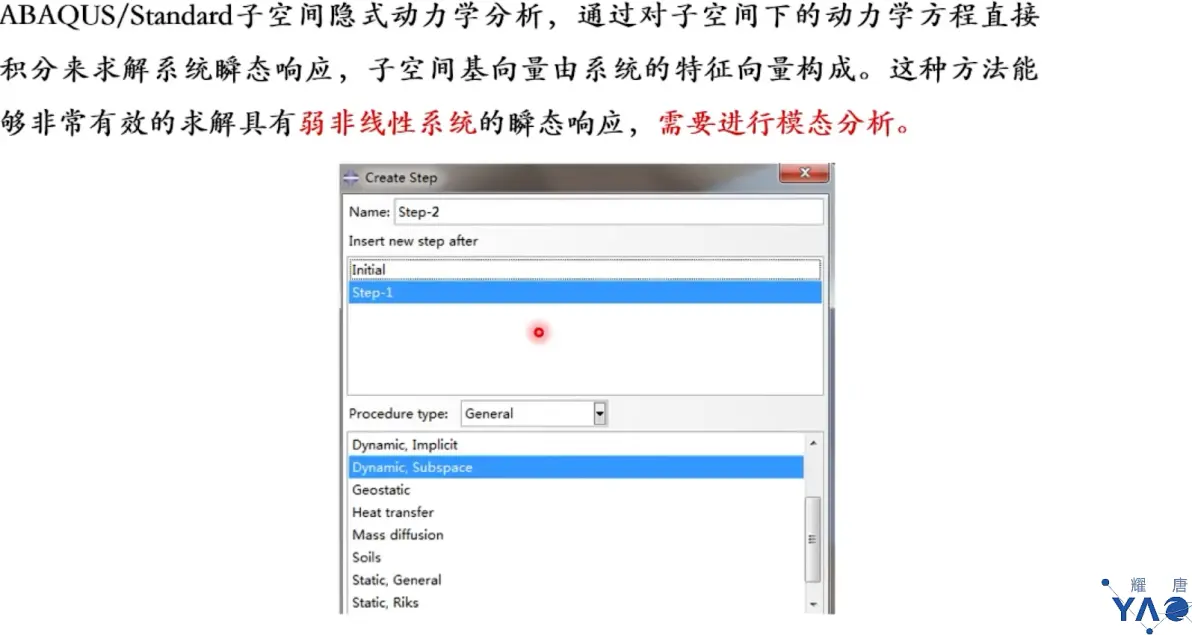
弱非线性系统（线性），需进行模态分析

模态瞬态动力学分析

显示动力学

时间步长要求

非线性严酷时，步长ITS降低或采用显示动力学方法进行计算

显示动力学：网格要求高，拉格朗日法居多

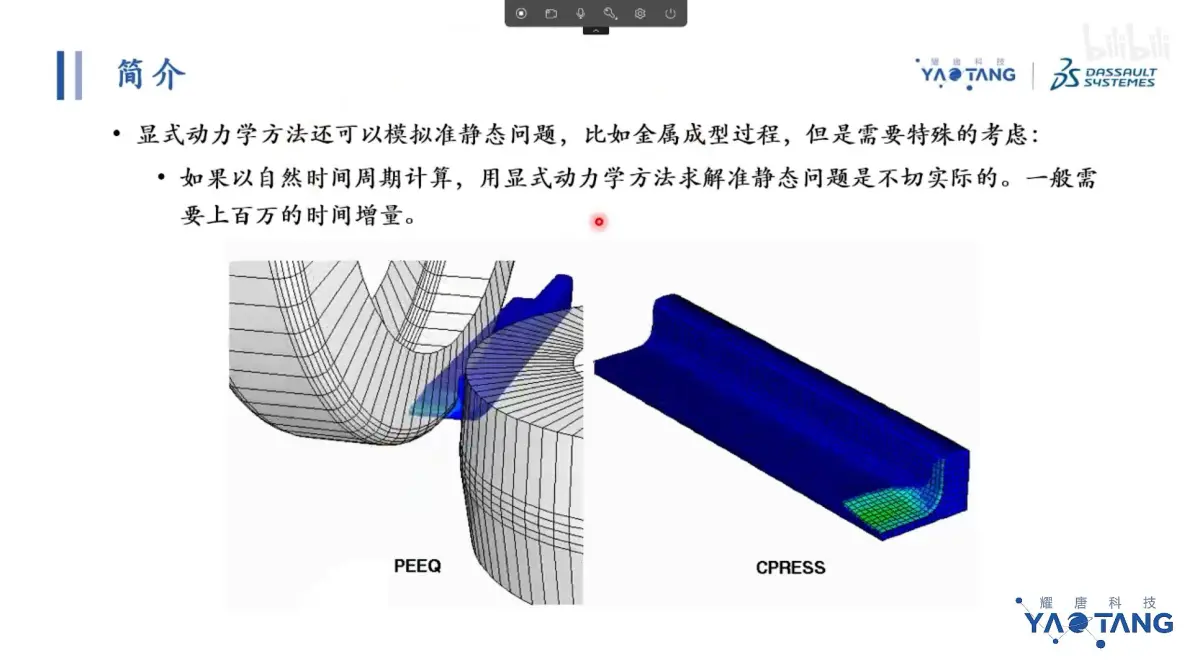
显示动力学可求解准静态问题：时间增量需求较大，用自然时间计算不切实际

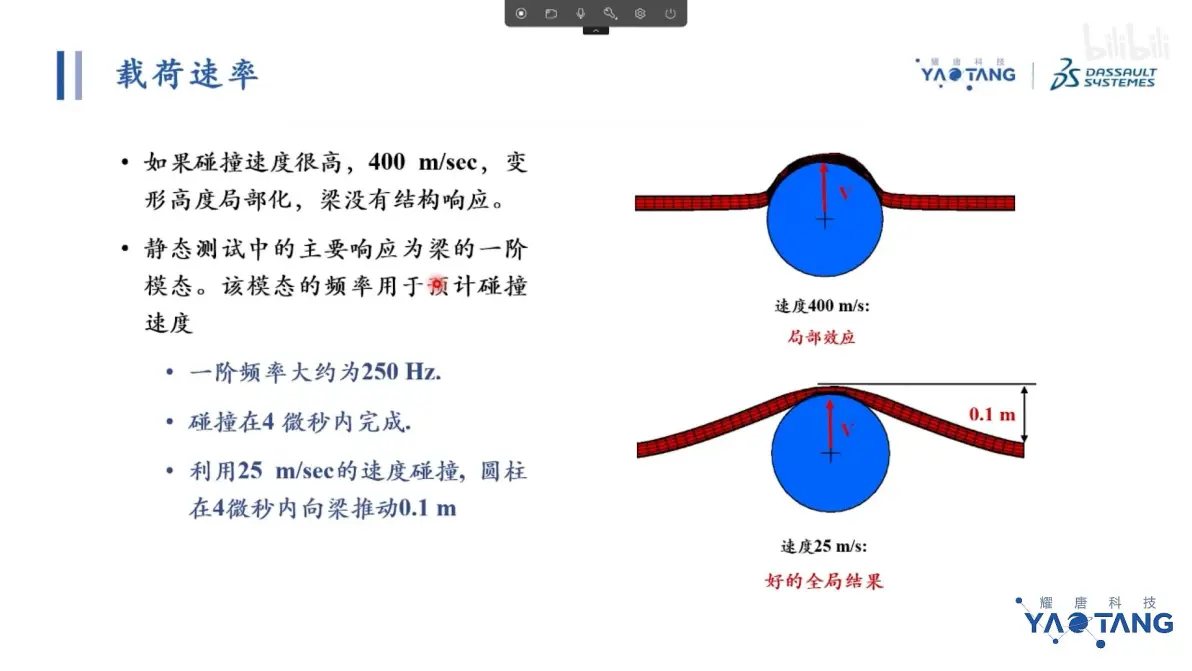
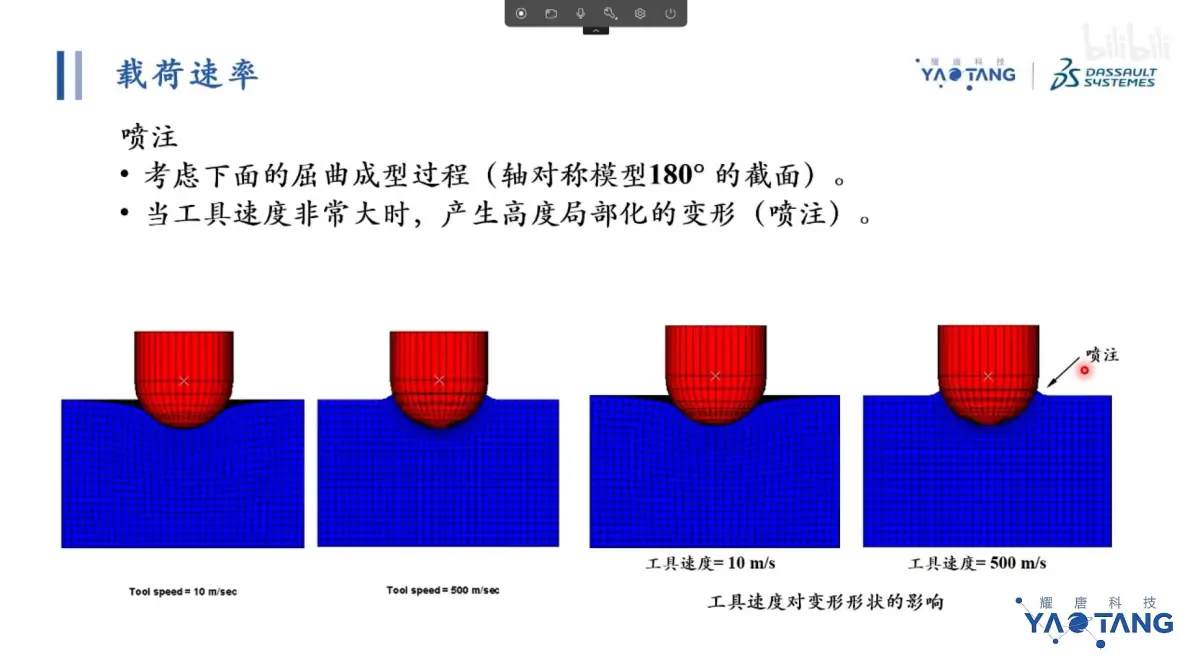
载荷速率：为节省计算时间提高进给速度，静态平衡问题演化为动平衡问题，惯性力影响增加，降低惯性力影响前提下，提升进给速度

金属成型1m/s,采用膨胀波速的1%（钢波速5000m/s）

喷注现象不能出现，惯性力较大

极限估算公式，Le最小特征单元长度

膨胀波速计算方式

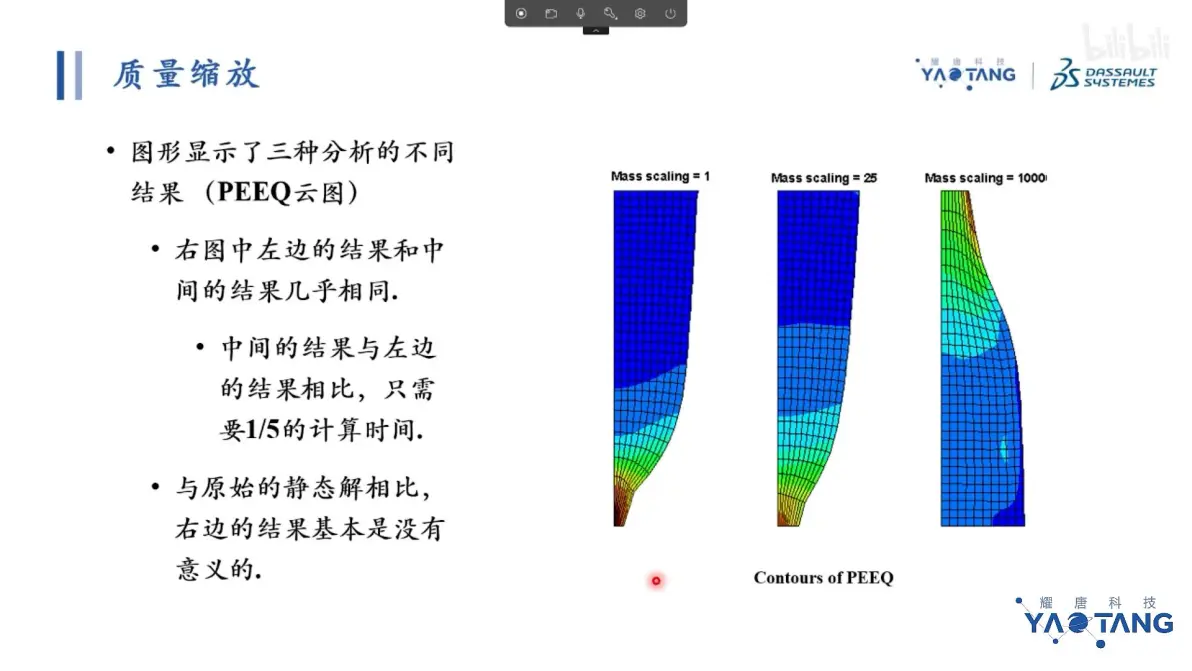
质量缩放控制在5%

质量缩放比例25稳定，过度增大就会失真

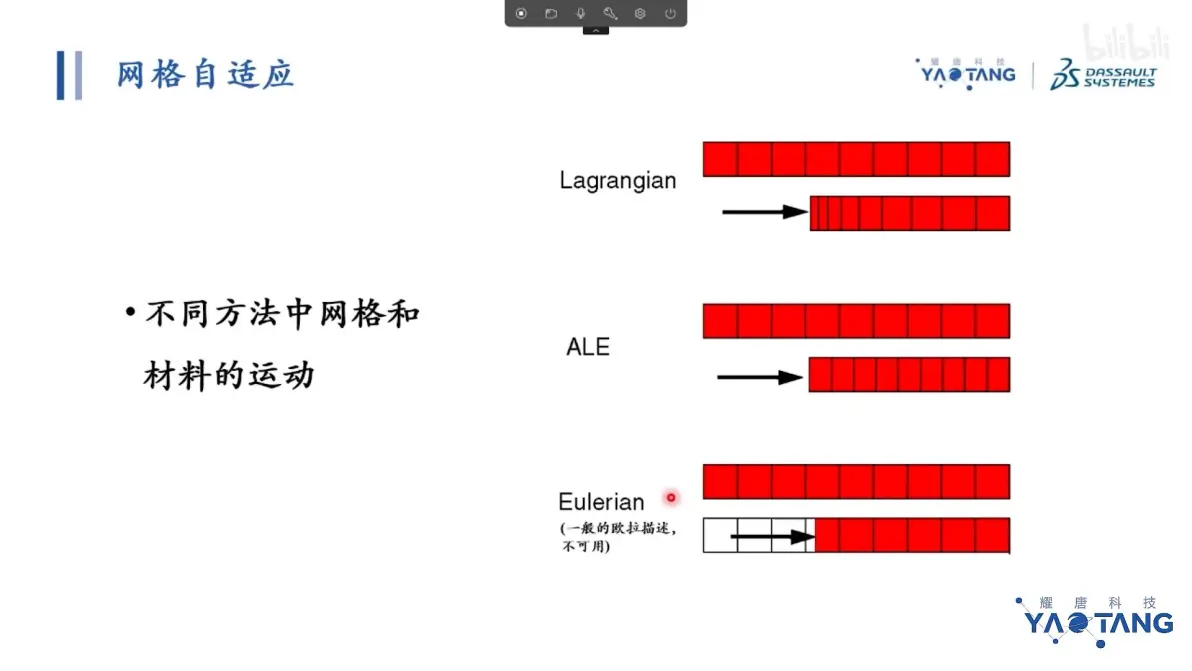
网格自适应：周期性减小王哥哥扭曲ALE模式

运用场合：动力冲击

网格定期平滑，保持网格长宽比

网格连接关系不变

ALE任意的拉格朗日－欧拉方法

网格运动不同模式

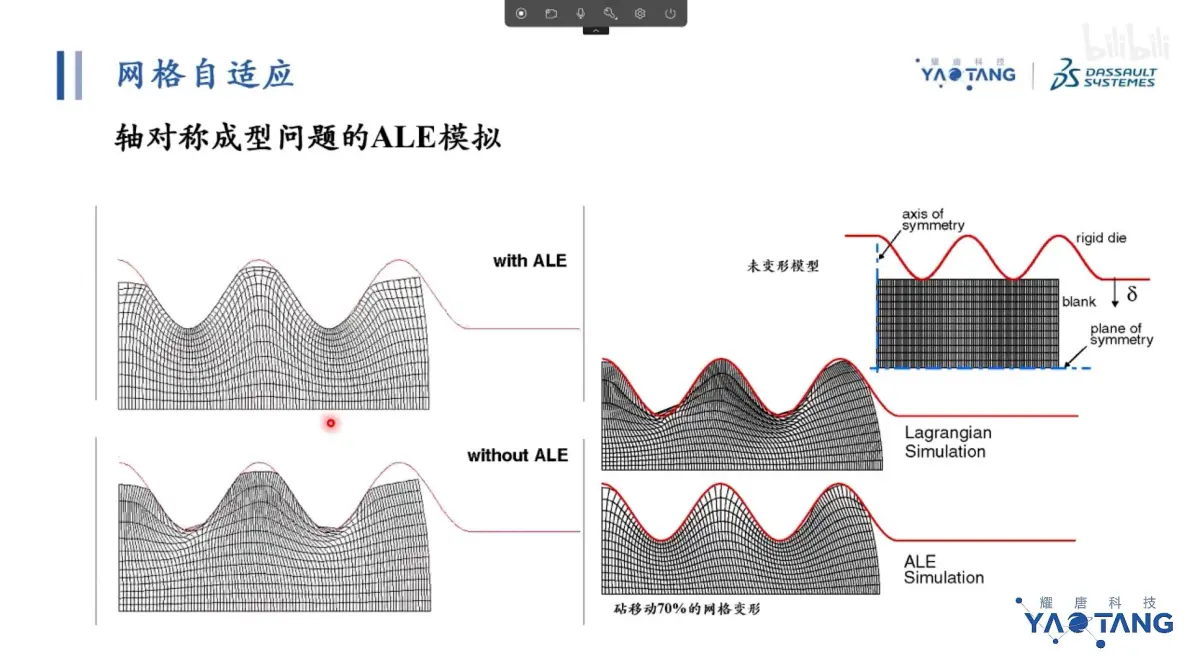
没有ALE，计算无法进行，运用ALE方式且网格质量保持较高，降低计算效率，多用于壳单元。体单元效率极低无法正常使用

总结：载荷大，显著惯性效应

速度小于波速１％，斜坡方式，由０增加加载速率，提高准静态响应准确性