1、带有条件约束的最短路径问题
最短路径问题是图论中求两个顶点之间的最短路径问题,通常是求最短加权路径。
条件最短路径,指带有约束条件、限制条件的最短路径。例如,顶点约束,包括必经点或禁止点的限制;边的约束,包括必经路段或禁止路段;还包括无权路径长度的限制,即经过几步到达终点。进一步地,还有双目标限制的最短路径问题,求最短距离中花费最小的路线;交通限制条件下的最短路径问题,需要考虑转向限制和延误的约束。
求解带有限制条件的最短路径问题,总体来说可以分为两类基本方法:一类是基于不带限制条件的最短路径算法,对求解过程中的每一条有效路径,都用限制条件进行判断,如果满足所有限制条件则继续,如果不满足限制条件则放弃该路径;另一类方法是基于具体问题和选择算法的特点,将问题转化为有约束的规划问题来处理。
但是,如果使用 NetworkX 求解带有限制条件的最短路径问题,采用这两类方法都会有一些困难。原因在于前文所介绍的 NetworkX 提供的 Dijkstra 算法、Bellman-Ford 算法、Floyd 算法和启发式算法 A* 都是封装函数,没有提供设置约束条件的选项和接口,因此用户不能把条件判断语句加入这些封装函数的程序内部。这种问题不仅存在于 Python 语言的 Network 工具包,对于其它计算机语言的工具包也是类似的:自己编程序费时费力,但可以根据需要修改和扩展;直接调用工具包的算法函数非常方便,但不能进行修改或扩展。
不过,NetworkX 可以生成两个顶点之间的所有简单路径,而且可以获得所有简单路径的边的列表。利用简单路径算法,可以通过对约束条件的判断来求解带有顶点约束和边约束的最短路径问题。
2、问题案例:蚂蚁的最优路径分析
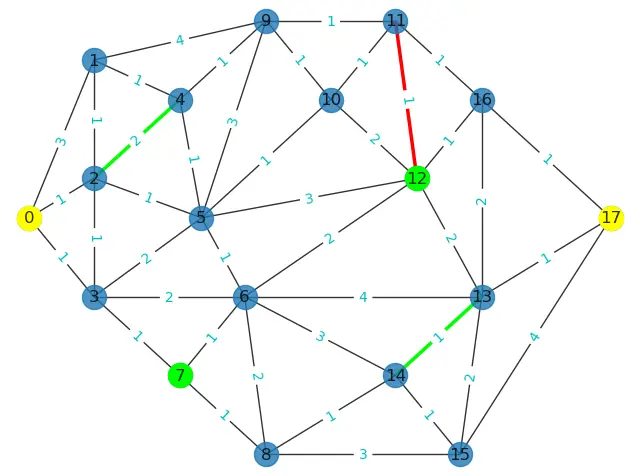
蚁巢有若干个储藏间(图中圆圈表示),储藏间之间有路径相连(路径拓扑结构如图所示)。该图为无向图,路径通行的花费如图中线路上的数字所示,路径正反方向通行的花费相同。要求从起点 N0 到终点 N17 的最优路径,并需要满足限制条件:
- 需要尽可能以最少的花费到达终点;
- 必须经过图中的绿色节点;
- 必须经过图中的两段绿色路段;
- 必须避开图中的红色路段。
说明:本案例出自西安邮电大学第12届数学建模竞赛赛题,本文进行了改编。
欢迎关注 Youcans 原创系列(https://www.jianshu.com/u/5df8372991c5)
3、NetworkX 求解带有条件约束的最短路径问题
3.1 图的创建和可视化
Python 例程(NetworkX)
# networkX_E3.py
# Demo of shortest path with NetworkX
# Copyright 2021 YouCans, XUPT
# Crated:2021-05-20
import matplotlib.pyplot as plt # 导入 Matplotlib 工具包
import networkx as nx # 导入 NetworkX 工具包
# 问题 1:蚂蚁的最优路径分析(西安邮电大学第12届数学建模竞赛B题)
gAnt = nx.Graph() # 创建:空的 无向图
gAnt.add_weighted_edges_from([(0,1,3),(0,2,1),(0,3,1),
(1,2,1),(1,4,1),(1,9,4),
(2,3,1),(2,4,2),(2,5,1),
(3,5,2),(3,6,2),(3,7,1),
(4,5,1),(4,9,1),
(5,6,1),(5,9,3),(5,10,1),(5,12,3),
(6,7,1),(6,8,2),(6,12,2),(6,13,4),(6,14,3),
(7,8,1),
(8,14,1),(8,15,3),
(9,10,1),(9,11,1),
(10,11,1),(10,12,2),
(11,12,1),(11,16,1),
(12,13,2),(12,16,1),
(13,14,1),(13,15,2),(13,16,2),(13,17,1),
(14,15,1),
(15,17,4),
(16,17,1)]) # 向图中添加多条赋权边: (node1,node2,weight)
pos={0:(1,8),1:(4,12),2:(4,9),3:(4,6),4:(8,11),5:(9,8), # 指定顶点位置
6:(11,6),7:(8,4),8:(12,2),9:(12,13),10:(15,11),11:(18,13),
12:(19,9),13:(22,6),14:(18,4),15:(21,2),16:(22,11),17:(28,8)}
nx.draw(gAnt, pos, with_labels=True, alpha=0.8)
labels = nx.get_edge_attributes(gAnt,'weight')
nx.draw_networkx_edge_labels(gAnt,pos,edge_labels=labels, font_color='c') # 显示权值
nx.draw_networkx_nodes(gAnt,pos,nodelist=[0,17],node_color='yellow') # 设置顶点颜色
nx.draw_networkx_nodes(gAnt,pos,nodelist=[7,12],node_color='lime') # 设置顶点颜色
nx.draw_networkx_edges(gAnt,pos,edgelist=[(2,4),(13,14)],edge_color='lime',width=2.5) # 设置边的颜色
nx.draw_networkx_edges(gAnt,pos,edgelist=[(11,12)],edge_color='r',width=2.5) # 设置边的颜色
plt.show()
运行结果
本段程序绘制网络图,包括顶点、边、边的权值,特殊顶点和特殊边的颜色设置。
程序说明
- 图的创建。本例使用 nx.Graph() 创建无向图,然后用 gAnt.add_weighted_edges_from() 函数以列表向图中添加多条赋权边,每个赋权边以元组 (node1,node2,weight) 表示。
- 图的绘制。使用nx.draw()绘图时,默认的节点位置并不理想,可以使用 pos 属性参数指定节点位置。pos 为字典数据类型,按 node:(x_pos,y_pos) 格式设置节点位置。
- 显示边的权值。使用 nx.draw_networkx_edge_labels() 可以绘制边的属性,本例中选择显示权值属性。
- 设置顶点属性。nx.draw_networkx_nodes() 可以设置顶点的属性,例如对 nodelist 列表中的节点设置颜色属性 node_color。
- 设置边的属性。nx.draw_networkx_edges() 可以设置边的属性,例如对 edgelist 列表中的边设置线宽属性 width 和颜色属性 edge_color。
3.2 无限制条件的最短路径
程序说明
- 对于无限制条件的最短路径问题,NetworkX 提供了 Dijkstra 算法、Bellman-Ford 算法、Floyd 算法和启发式算法 A* 的函数。
- 例程使用 nx.dijkstra_path() 和 nx.dijkstra_path_length() 调用 Dijkstra 算法求两个指定顶点之间的最短加权路径和最短加权路径长度。
Python 例程(NetworkX)
# 两个指定顶点之间的最短加权路径
minWPath1 = nx.dijkstra_path(gAnt, source=0, target=17) # 顶点 0 到 顶点 17 的最短加权路径
# 两个指定顶点之间的最短加权路径的长度
lMinWPath1 = nx.dijkstra_path_length(gAnt, source=0, target=17) #最短加权路径长度
print("\n问题1: 无限制条件")
print("S 到 E 的最短加权路径: ", minWPath1)
print("S 到 E 的最短加权路径长度: ", lMinWPath1)
运行结果
问题1: 无限制条件
S 到 E 的最短加权路径: [0, 2, 5, 10, 11, 16, 17]
S 到 E 的最短加权路径长度: 6
3.3 限制条件:禁止点或禁止边
程序说明
- 禁止点或者禁止边的处理比较简单,从图中删除对应的禁止顶点或禁止边即可。当然,在创建图时就不添加这些顶点和边更简单,但这样在绘图时也无法反映这些顶点和边。
- 使用 remove_node(n) 删除指定顶点 n,remove_edge(u,v) 删除指定的边 (u,v)。
- 使用 remove_nodes_from([n1,...nk]) 删除多个顶点,remove_edges_from([(u1,v1),...(uk,vk)]) 删除多条边。
- 例程




