机器学习入门：TensorFlow与Mnist数据集

训练一个机器学习模型用于预测图片里面的数字。

登录后复制

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data

import matplotlib.pyplot as plt
import numpy as np

mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
# 获取数数据集
x = tf.placeholder("float", [None, 784])
# 占位符
W = tf.Variable(tf.zeros([784,10]))
# 变量variable，需要训练得到的数据
b = tf.Variable(tf.zeros([10]))
y = tf.nn.softmax(tf.matmul(x,W) + b)
# 占位符
y_ = tf.placeholder("float", [None,10])
# 交叉熵
cross_entropy = -tf.reduce_sum(y_*tf.log(y))

# 训练过程，梯度下降法，梯度0.01，损失函数最小值
train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cross_entropy)
# 初始化
init = tf.initialize_all_variables()
sess = tf.Session()
sess.run(init)
# 随机获取100组数据
batch_xs, batch_ys = mnist.train.next_batch(100)
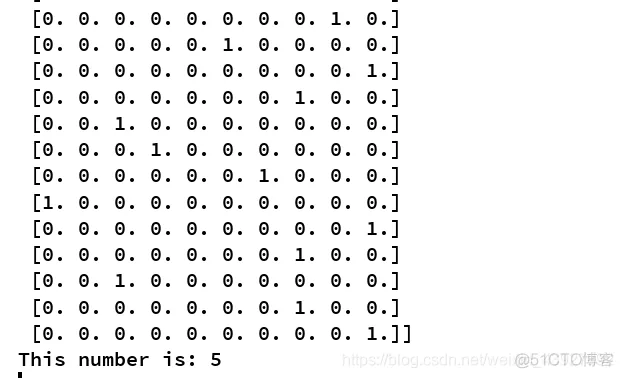
# 打印第二张图片的像素信息和这100组数据对应的lable
print(batch_xs[1],batch_ys,sep='\n')
# 求第二组数据所对应的label排序
index=np.argsort(batch_ys[1])
# 打印第二组数据的真实值
print('This number is:',str(index[-1]))
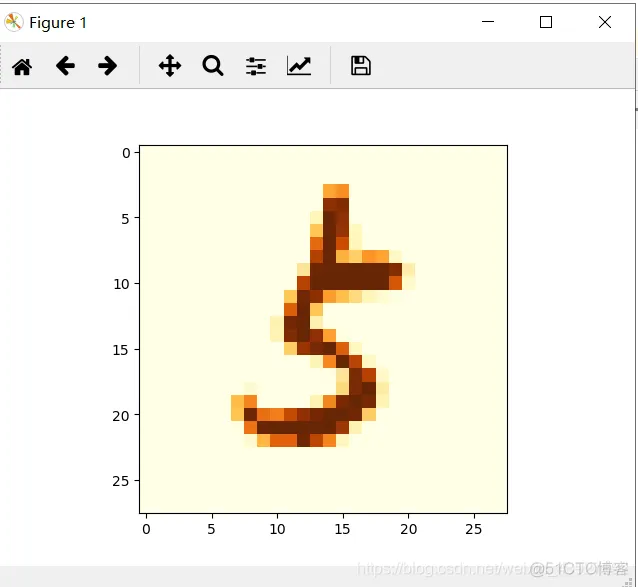
# 将第二张图片显示出来
a=batch_xs[1].reshape(28,28)
plt.imshow(a,cmap=plt.get_cmap('YlOrBr'))
plt.show()

# 下面是准确度计算
# for i in range(1000):
#   batch_xs, batch_ys = mnist.train.next_batch(100)
#   sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})
#
# correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
# accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
# print (sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels}))

关于Softmax函数

登录后复制

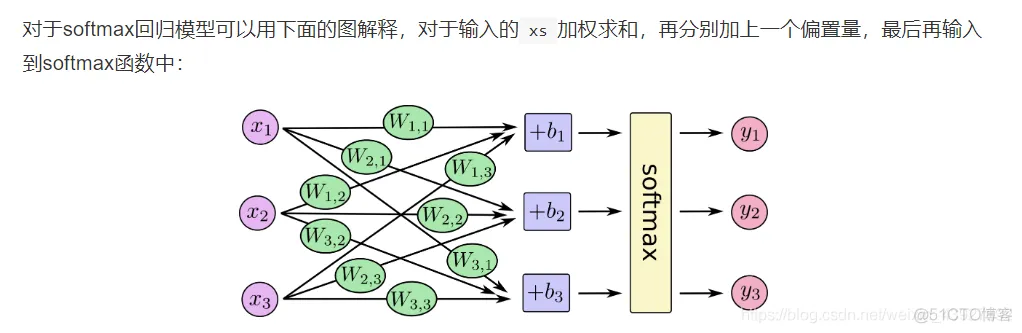
softmax回归分两步：
第一步：为了得到一张给定图片属于某个特定数字类的证据（evidence）,
我们对图片像素值进行加权求和。如果这个像素具有很强的证据说明这张图片
不属于该类，那么相应的权值为负数，相反，如果这个像素拥有很强的证据说明
这张图片属于该类，那么相应的权值为正数。





登录后复制

此外我们需要一个额外的偏置量，因为输入往往会带有一些无关的干扰量，
因此对于给定的输入图片x它代表的是数据i的证据可以表示为

evidencei= wij*xj+b
其中wi代表权重，b代表偏置量，j代表给定图片x的像素索引用于像素求和。
然后用softmax函数可以把这些证据转换成概率：y




登录后复制

这里的softmax可以看成一个激励（activation）函数或者链接函数（link）函数，
把我们定义的线性函数的输出转换成我们想要的格式，也就是关于10个数字类的概率分布。
因此给定一张图片他对于每一个数字的吻合度可以被softmax函数转换成一个概率值，
softmax函数可以定义为：

softmax(x)=normalize(exp(x))
这个公式表明，把输入值（即是证据）当作幂指数求值，
然后正则化这些结果值，证据越大，那么它所对应的假设模型里面的乘数权重值也就越大，
反之拥有更少的证据意味着在假设模型里面拥有更小的乘数系数。
softmax然后会正则化这些权重值，使他们的总和等于1，以此构造一个有效的概率分布。

以上就是softmax()函数的核心数学思想，还有具体的关于tf的操作后面还在学习！这一篇博客就是实现了使用tensorflow中的mnist数据集，并将像素转换成可视化的图片，对比是否识别成功！

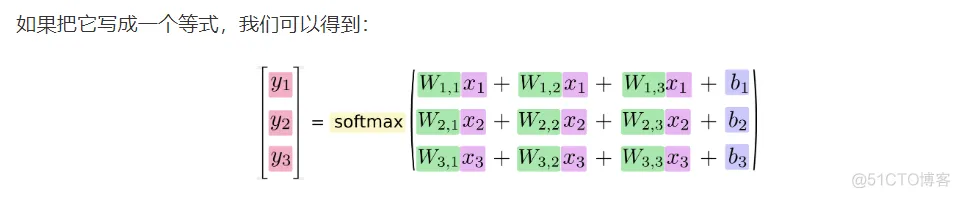
免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删