神经网络识别仿真实验：测试与验证流程

一、理论基础1.1基于BP神经网络的识别

BP神经网络，即Back Propagation神经网络，其本质是一种基于误差反馈传播的神经网络算法。从结构上讲，BP神经网络是由一个信息的正向传播网络和一个误差的反向传播网络两个模块构成。BP神经网络的基本结构如下图所示：

从图1的结构可知，BP神经网络主要由输入层，隐含层以及输出层构成。来自外界的信息通过输入层传输进入到隐含层进行处理，并由输出层输出处理结果。当BP神经网络的输出结果和其期望结果之间的误差较大的时候，则进入反向传播阶段，并进行进行审计网络权值的修正，直到输出结果和期望结果误差满足一定条件为止。

1.2基于RBF神经网络的识别

RBF网络是一种三层前向网络：

第一层为输入层，由信号源节点组成。

第二层为隐含层，隐单元的变换函数是一种局部分布的非负非线性函数，他对中心点径向对称且衰减。隐含层的单元数由所描述问题的需要确定。

第三层为输出层，网络的输出是隐单元输出的线性加权。

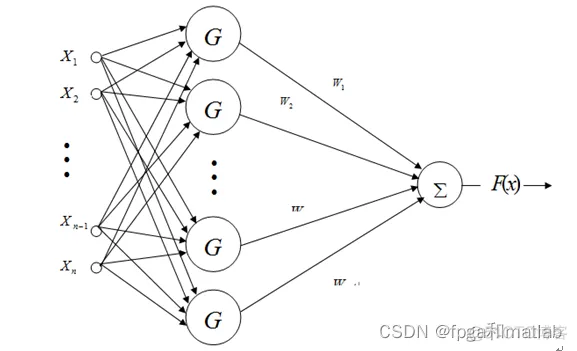
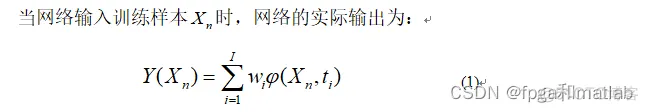
通常使用的RBF有：高斯函数、多二次函数(multiquadric function)、逆多二次函数、薄板样条函数等。普通RBF网络采用的是高斯函数。当“基函数”采用的高斯基函数具备如下的优点：

①表示形式简单，即使对于多变量输入也不增加太多的复杂性；

②径向对称；

③光滑性好，任意阶导数均存在；

④由于该基函数表示简单且解析性好，因而便于进行理论分析。

RBF网络具有良好的逼近任意非线性函数和表达系统内在的难以解析的规律性的能力，并且具有极快的学习收敛速度。基于径向基函数网络的上述优点，我们将其应用于对非线性函数的模拟当中。1.3基于GRNN神经网络的识别

GRNN，即General Regression Neural Network，中文全称为广义回归神经网络，是由The Lockheed Palo Alto研究实验室在1991年提出的。GRNN是一种新型的基于非线性回归理论的神经网络模型[43,44]。GRNN是建立在非参数核回归基础之上的，该神经网络是以测试样本为后验条件，并从观测样本中计算得到自变量和因变量之间的概率密度函数，然后在计算出因变量关于自变量的回归值。由于GRNN不需要规定模型的类型，只需要设置神经网络的光滑因子参数，GRNN神经网络的光滑因子参数的取值对神经网络的输出影响较大，当光滑因子参数较大的时候，其对应的神经元所覆盖的输入区域就越大；当光滑因子参数较小的时候，神经网络对应的径向基函数曲线较陡，因此神经网络输出结果更接近期望值，但此时光滑度越差。

由于GRNN广义回归神经网络是基于非线性核回归分析的神经网络，因此，对于任意一个非独立变量y，其相对于独立变量x的回归分析的过程是计算具有最大概率值y。现假设随机变量x和y的联合概率密度函数为f (x ,y)，已知x的观测值为X，则y相对于X的回归，即条件均值为：

GRNN结构如图所示，整个网络包括输入层、模式层、求和层与输出层。

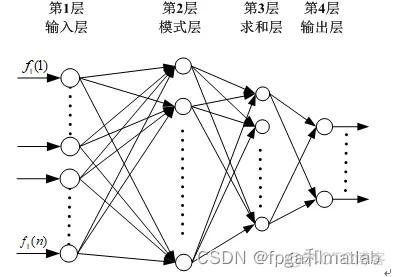
  从结构图可知，GRNN神经网络的输入层神经元数目和输入样本的维度是相同的，即每一个神经元将输入信号直接传递给GRNN神经网络的隐含层中。二、核心程序

clc;clear;close all;warning off;addpath 'func\'%%%选择神经网络类型;%1：BP神经网络%2：GRNN神经网络%3：RBF神经网络SEL = 2;load data.mat%检测航迹的异常端，这里通过对数据航迹进行分段处理，分析每一段的特征，并通过神经网络进行识别%分段检测长度Len = 50;Features = cell(1,50);Features2= [];for i = 1:50    i    %每段航迹进行等比例划分     tmps    = Datas{i};    Feature = [];    for j = 1:floor(length(tmps)/Len)        tmps2   = tmps(Len*(j-1)+1:Len*j,:);        %特征提取        Feature = [Feature;[func_feature1(tmps2(:,1)),func_feature1(tmps2(:,2))]];    end    Features{i} = Feature;    Features2   = [Features2;Feature];end%异常和正常分类load fenlei.mat%这个是自己首先做的人工区分，分为正常和异常两类Lend = length(cidx)index= randperm(Lend);Type1 = [];Type2 = [];for i = 1:floor(0.8*length(cidx))    if cidx(index(i)) == 1       Type1 = [Type1;Features2(index(i),:)];    else       Type2 = [Type2;Features2(index(i),:)];    endend%训练器，随机选择一部分进行训练Train_data = [Type1;Type2];Train_Label= [ones(1,length(Type1)),2*ones(1,length(Type2))]';%%if  SEL == 1    %1:bp网络    net = newff(Train_data',Train_Label',128);    net.trainParam.epochs   = 60;    %训练次数     net.trainParam.goal     = 1e-4;   %误差期望值     net.trainParam.mu       = 0.01;   %定义神经网络学习率    net.trainParam.min_grad = 1e-8;   %定义神经网络最小梯度值    %returns of the train:     %net--New network     %tr--Training record (epoch and perf).     %Y--Network outputs.     %E--Network errors.     [net,tr,Y,E] = train(net,Train_data',Train_Label');     save Net_BP.mat netendif  SEL == 2    %GRNN    net      = newgrnn(Train_data',Train_Label',0.000025);    save Net_GRNN.mat netendif  SEL == 3    %RBF    net      = newrb(Train_data',Train_Label',0.04);    save Net_RBF.mat netend三、仿真测试结果

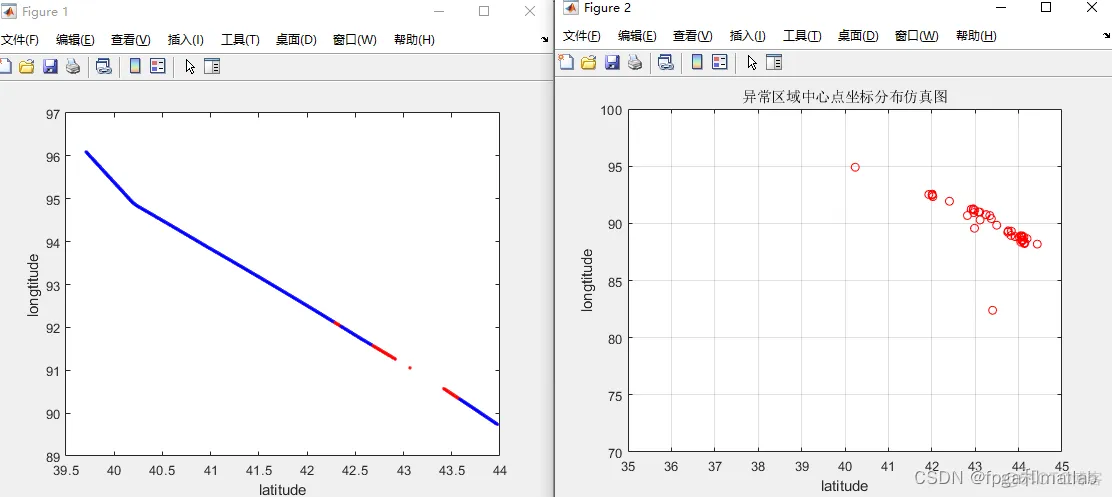
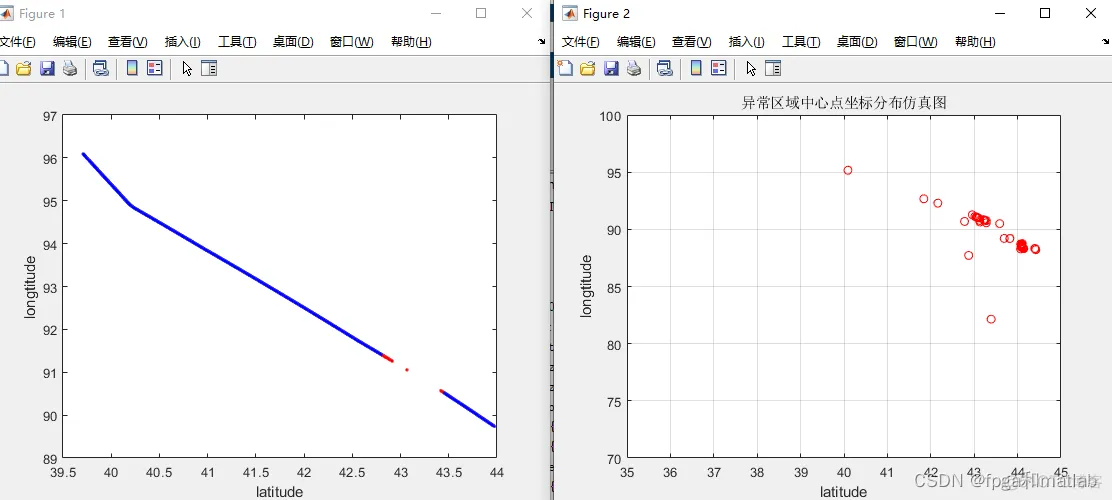
免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删