产品
这个部分，主要是通过给定模型的输入和输出，然后通过网络进行训练，得到神经网络的辨识参数。
对于网络辨识部分，其基本构架如下所示：
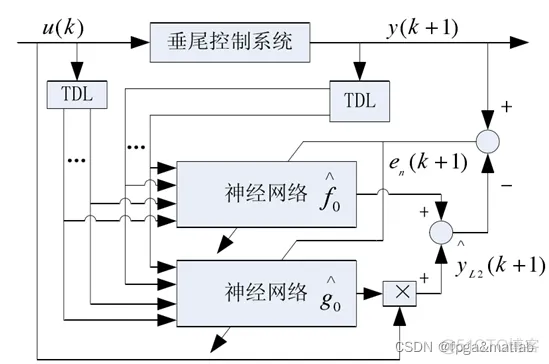
上述的辨识结构，通过控制对象的输入和输出的延迟分别进入F网络和G网络，然后通过网络输出和实际输出的误差对网络F和网络G进行在线学习。
具体理论论文讲的比较详细了，这里不再重复，仿真效果如下所示：
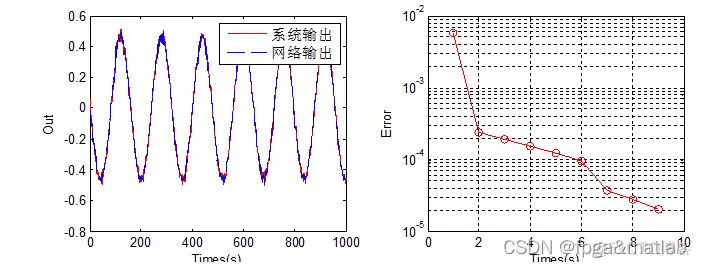
部分核心程序：
clc;
clear all;
close all;
warning off;
addpath 'func\'
pack;
Num_In = 6;
Num_Hidden = 12;
Num_Out = 1;
load func\result3.mat
[In,Out] = func_data(y3,y_out3);
parameter;
while Error>Err_goal & Iter < Max_iter
u_delay1 = 0;
u_delay2 = 0;
u_delay3 = 0;
u_delay4 = 0;
y_delay1 = 0;
y_delay2 = 0;
y_delay3 = 0;
y_delay4 = 0;
Err_tmp = 0;
for k=1:All_Length
Data_Delays = [y_delay1;
y_delay2;
y_delay3;
u_delay2;
u_delay3;
u_delay4];
%隐层求和
[Y_hidden(k),Hidden1G,Hidden2G,Y_hiddenG(k),Hidden1F,Hidden2F,Y_hiddenF(k)] = func_Hiddern(Data_Delays,u_delay1,Num_Hidden,G_wight_In,G_wight_Inb,G_wight_Out,G_wight_Outb,F_wight_In,F_wight_Inb,F_wight_Out,F_wight_Outb);
Err_tmp = Out(k)-Y_hidden(k);
%F和G网络
%G神经网络计算
[dg_weight_in,dg_bweight_in,dg_weight_out,dg_bweight_out] = func_G_net(Err_tmp,Out(k),In(k),Y_hidden(k),G_wight_Out,Hidden2G,Data_Delays,Y_hiddenG(k),Hidden1G,Num_Hidden,Num_In);
%F神经网络计算
[df_weight_in,df_bweight_in,df_weight_out,df_bweight_out] = func_F_net(Err_tmp,Out(k),In(k),Y_hidden(k),F_wight_Out,Hidden2F,Data_Delays,Y_hiddenG(k),Hidden1F,Num_Hidden,Num_In);
%G网络权值更新
[G_wight_In,G_wight_Out,G_wight_Inb,G_wight_Outb]=func_G_W_updata(Learn_Rate,alpha,...
G_wight_In1,G_wight_Out1,G_wight_Inb1,F_wight_Outb1,...
dg_weight_in,dg_weight_out,dg_bweight_in,dg_bweight_out,...
G_wight_Outb1,...
G_wight_In2,G_wight_Out2,G_wight_Inb2,G_wight_Outb2);
%F网络权值更新
[F_wight_In,F_wight_Out,F_wight_Inb,F_wight_Outb]=func_F_W_updata(Learn_Rate,alpha,...
G_wight_In1,F_wight_Out1,F_wight_Inb1,F_wight_Outb1,...
df_weight_in,df_weight_out,df_bweight_in,df_bweight_out,...
G_wight_In2,F_wight_Out2,F_wight_Inb2,F_wight_Outb2);
%延迟
u_delay4 = u_delay3;
u_delay3 = u_delay2;
u_delay2 = u_delay1;
u_delay1 = In(k);
y_delay4 = y_delay3;
y_delay3 = y_delay2;
y_delay2 = y_delay1;
y_delay1 = Out(k);
G_wight_In2 = G_wight_In1;
G_wight_In1 = F_wight_In;
F_wight_Out2 = F_wight_Out1;
F_wight_Out1 = F_wight_Out;
F_wight_Inb2 = F_wight_Inb1;
F_wight_Inb1 = F_wight_Inb;
F_wight_Outb2 = F_wight_Outb1;
F_wight_Outb1 = F_wight_Outb;
G_wight_In2 = G_wight_In1;
G_wight_In1 = G_wight_In;
G_wight_Out2 = G_wight_Out1;
G_wight_Out1 = G_wight_Out;
G_wight_Inb2 = G_wight_Inb1;
G_wight_Inb1 = G_wight_Inb;
G_wight_Outb2 = G_wight_Outb1;
G_wight_Outb1 = G_wight_Outb;
end
Error = sum((Out-Y_hidden).^2)/k;
Error2(Iter) = Error;
%如果当前训练误差反而增加，则放弃此次训练结果，重新训练
if (Iter > 1) & (Error2(Iter) > 1.2*Error2(Iter-1))
Iter = Iter;
Break_cnt = Break_cnt + 1;
if Break_cnt > 20
Error2(Iter) = [];
break;
end
else
Break_cnt = 0;
Iter = Iter+1;
fprintf('迭代次数：%d ',Iter);
fprintf('误差：%f',Error);
fprintf('\n\n');
end
end
figure;
subplot(121);
plot(Times(1:1000),Out(1:1000),'r');
hold on;
plot(Times(1:1000),Y_hidden(1:1000),'b--');
hold on;
xlabel('Times(s)');
ylabel('Out');
legend('系统输出','网络输出');
subplot(122);
semilogy(1:length(Error2),Error2,'r-o');
xlabel('Times(s)');
ylabel('Error');
grid on;
F_wight_In0 = F_wight_In;
F_wight_Out0 = F_wight_Out;
G_wight_In0 = G_wight_In;
G_wight_Out0 = G_wight_Out;
F_wight_Inb0 = F_wight_Inb;
F_wight_Outb0 = F_wight_Outb;
G_wight_Inb0 = G_wight_Inb;
G_wight_Outb0 = G_wight_Outb;
save NN_reg_signal3.mat F_wight_In0 F_wight_Out0 G_wight_In0 G_wight_Out0 F_wight_Inb0 F_wight_Outb0 G_wight_Inb0 G_wight_Outb0
A08-16
免责声明：本文系网络转载或改编，未找到原创作者，版权归原作者所有。如涉及版权，请联系删
155-2731-8020
